• 统计生成模型的参数估计
  – Maximum Likelihood(ML) 假设参数是某个确定的值，通过使似然度最大求出参数
  – Bayesian estimation 假设参数是随机变量，估计参数分布的参数
  – 最大似然求出具体的参数，贝叶斯求的是参数的分布

最大似然估计

• 假设概率密度函数 $p\left(x\mid {\omega }_i,{\theta }_i\right),{\theta }_i$ to be estimated，估计每一类的概率密度函数，${\theta }_i$就是每一类概率密度函数的待估计参数
• 样本数据 $D_1,\dots ,D_c$，假设每一类$D_i$中的样本满足独立同分布i.i.d
• 总体流程就是从每一类中估计出一个概率密度函数，组成分类器
  

如何估计每一类的参数

• 似然函数（在某种参数下得到现有样本的概率，并应用独立同分布条件）
  $$p(\mathcal{D}\mid \mathbf{\theta })=\prod _{k=1}^{n}p\left({\mathbf{x}}_k\mid \mathbf{\theta }\right)$$
• 求使得似然函数最大化的参数（可能有解析解；如果没有可以考虑用梯度下降或其他优化方法）
  $$\underset{\mathbf{\theta }}{\max }p(D\mid \mathbf{\theta })\leftrightarrow {\nabla }_{\mathbf{\theta }}p(D\mid \mathbf{\theta })=0$$
  $${\nabla }_{\mathbf{\theta }}\equiv \left[\begin{array}{c}\frac{\partial }{\partial {\theta }_1}\\ ⋮\\ \frac{\partial }{\partial {\theta }_p}\end{array}\right]$$
  
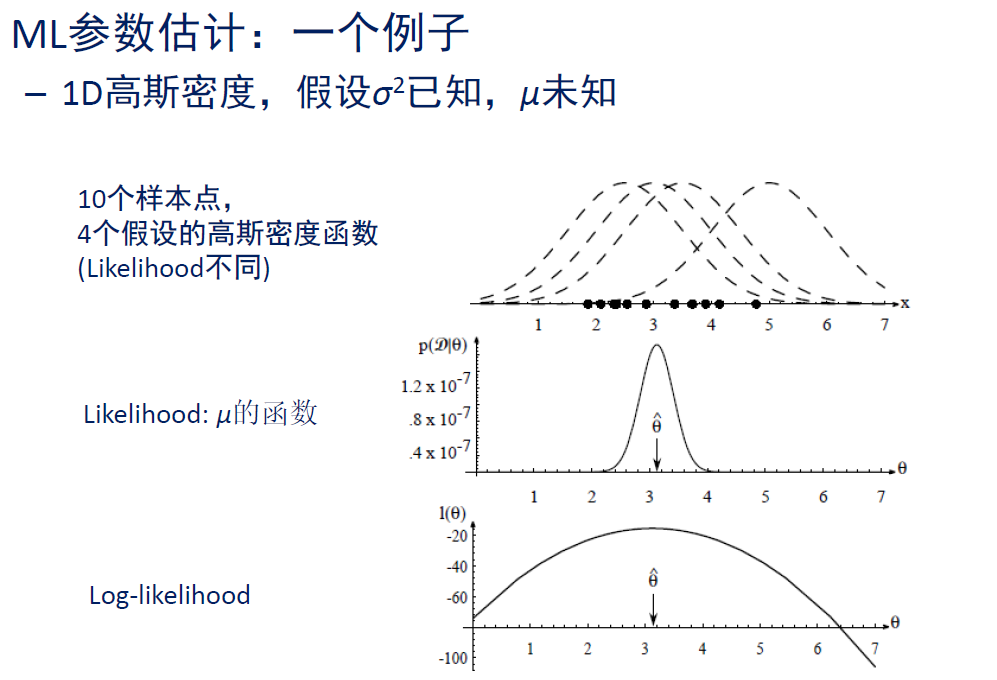
• 似然度通常取对数，这样比较好算（累乘变累加），也就是对数似然度
  $$l(\mathbf{\theta })\equiv \ln p(\mathcal{D}\mid \mathbf{\theta })l(\mathbf{\theta })=\sum _{k=1}^n\ln p\left({\mathrm{x}}_k\mid \mathbf{\theta }\right)$$
• ML估计
  $$\begin{array}{rl}& \hat{\mathbf{\theta }}=\arg \underset{\mathbf{\theta }}{\max }l(\mathbf{\theta })\\ & {\nabla }_{\mathbf{\theta }}l=\sum _{k=1}^n{\nabla }_{\mathbf{\theta }}\ln p\left({\mathrm{x}}_k\mid \mathbf{\theta }\right)=0\\ & \frac{\partial l}{\partial {\theta }_j}=0,j=1,\dots ,p\end{array}$$

【例子】假设样本服从高斯分布，但是均值$\mu$未知

• 单个样本的对数似然度极其梯度
  $$\begin{array}{c}\ln p\left({\mathrm{x}}_k\mid \mathbf{\mu }\right)=-\frac{1}{2}\ln \left[(2\pi {)}^d|\mathbf{\Sigma }|\right]-\frac{1}{2}{\left({\mathrm{x}}_k-\mathbf{\mu }\right)}^t{\mathbf{\Sigma }}^{-1}\left({\mathrm{x}}_k-\mathbf{\mu }\right)\\ {\nabla }_{\mathbf{\theta }}\ln p\left({\mathrm{x}}_k\mid \mathbf{\mu }\right)={\mathbf{\Sigma }}^{-1}\left({\mathrm{x}}_k-\mathbf{\mu }\right)\end{array}$$
• 令梯度为0，可以看到均值的最大似然估计就是样本均值
  $$\begin{array}{rl}{\nabla }_{\mathbf{\theta }}l(\mathbf{\theta })=0& \Rightarrow \sum _{k=1}^n{\mathbf{\Sigma }}^{-1}\left({\mathrm{x}}_k-\hat{\mathbf{\mu }}\right)=0\\ & \Rightarrow \hat{\mu }=\frac{1}{n}\sum _{k=1}^n{\mathrm{x}}_k\end{array}$$

【例子】假设样本服从高斯分布，但是均值$\mu$和协方差矩阵$\Sigma$均未知
（1）假设一维情况：${\theta }_1=\mu$ and ${\theta }_2={\sigma }^2$

• 单样本对数似然度
  $$\ln p\left(x_k\mid \mathbf{\theta }\right)=-\frac{1}{2}\ln 2\pi {\theta }_2-\frac{1}{2{\theta }_2}{\left(x_k-{\theta }_1\right)}^2$$
• 对参数求梯度
  $${\nabla }_{\mathbf{\theta }}l={\nabla }_{\mathbf{\theta }}\ln p\left(x_k\mid \mathbf{\theta }\right)=\left[\begin{array}{c}\frac{1}{{\theta }_2}\left(x_k-{\theta }_1\right)\\ -\frac{1}{2{\theta }_2}+\frac{{\left(x_k-{\theta }_1\right)}^2}{2{\theta }_2^2}\end{array}\right]$$
• 令梯度为0，解方程得
  $$\begin{array}{rl}{\nabla }_{\mathbf{\theta }}l(\mathbf{\theta })& =0\Rightarrow \sum _{k=1}^n\frac{1}{{\hat{\theta }}_2}\left(x_k-{\hat{\theta }}_1\right)=0\Rightarrow \hat{\mu }=\frac{1}{n}\sum _{k=1}^n{x}_k\\ -\sum _{k=1}^n\frac{1}{{\hat{\theta }}_2}& +\sum _{k=1}^n\frac{{\left(x_k-\widehat{{\theta }_1}\right)}^2}{{\hat{\theta }}_2^2}=0\Rightarrow {\hat{\sigma }}^2=\frac{1}{n}\sum _{k=1}^n{\left(x_k-\hat{\mu }\right)}^2\end{array}$$
• 这个估计是有偏估计，但是我忘记怎么证了（手动狗头），本科概率论有讲
  $$\mathcal{E}\left[\frac{1}{n}\sum _{i=1}^n{\left(x_i-\bar{x}\right)}^2\right]=\frac{n-1}{n}{\sigma }^2\ne {\sigma }^2$$

（2）多变量情形
$$\begin{array}{rl}{\nabla }_{\mathbf{\theta }}l& =\sum _{k=1}^n{\nabla }_{\mathbf{\theta }}\ln p\left({\mathrm{x}}_k\mid \mathbf{\theta }\right)=0\\ \hat{\mu }& =\frac{1}{n}\sum _{k=1}^n{\mathrm{x}}_k\\ \hat{\mathbf{\Sigma }}& =\frac{1}{n}\sum _{k=1}^n\left({\mathrm{x}}_k-\hat{\mathbf{\mu }}\right){\left({\mathrm{x}}_k-\hat{\mathbf{\mu }}\right)}^t\end{array}$$

• 无偏估计应该是这样的，但是实际差别不大
  $$\begin{array}{rl}& \mathcal{E}\left[\frac{1}{n-1}\sum _{i=1}^n{\left(x_i-\bar{x}\right)}^2\right]={\sigma }^2\\ & \mathbf{C}=\frac{1}{n-1}\sum _{k=1}^n\left({\mathbf{x}}_k-\hat{\mathbf{\mu }}\right){\left({\mathrm{x}}_k-\hat{\mathbf{\mu }}\right)}^t\end{array}$$

贝叶斯参数估计

• 后验概率（全概率公式，后面都带一个$\mathcal{D}$，代表样本集）
  $$P\left({\omega }_i\mid \mathbf{x},\mathcal{D}\right)=\frac{p\left(\mathbf{x}\mid {\omega }_i,\mathcal{D}\right)P\left({\omega }_i\mid \mathcal{D}\right)}{{\sum }_{j=1}^{c}p\left(\mathbf{x}\mid {\omega }_j,\mathcal{D}\right)P\left({\omega }_j\mid \mathcal{D}\right)}$$
• 假设先验概率和样本无关
  $$P\left({\omega }_i\mid \mathbf{x},\mathcal{D}\right)=\frac{p\left(\mathbf{x}\mid {\omega }_i,{\mathcal{D}}_i\right)P\left({\omega }_i\right)}{{\sum }_{j=1}^{c}p\left(\mathbf{x}\mid {\omega }_j,{\mathcal{D}}_j\right)P\left({\omega }_j\right)}$$
• 我们已知样本集$\mathcal{D}$，去估计$\mathbf{x}$
  $$\begin{array}{rl}p(\mathbf{x}\mid \mathcal{D})& =\int p(\mathbf{x},\mathbf{\theta }\mid \mathcal{D})d\theta \\ & =\int p(\mathbf{x}\mid \mathbf{\theta })\underline{p(\mathbf{\theta }\mid \mathcal{D})}d\mathbf{\theta }\end{array}$$
• 我们知道$p(\mathbf{x}\mid \mathbf{\theta })$，但不知道$p(\mathbf{\theta }\mid \mathcal{D})$，这就是贝叶斯估计要解的问题，咱们是在已知样本集的情况下，去估计未知参数的分布$p(\mathbf{\theta }\mid \mathcal{D})$

高斯密度贝叶斯估计

• 一维情况估计$p(\mathbf{\theta }\mid \mathcal{D})$
• 假设样本服从高斯分布$p(x\mid \mu )\sim N\left(\mu ,{\sigma }^2\right)$，假设均值也服从高斯分布$p(\mu )\sim N\left({\mu }_0,{\sigma }_0^2\right)$，$p(D\mid \mu )={\prod }_{k=1}^{n}p\left(x_k\mid \mu \right)$
  $$\begin{array}{rlr}p(\mu \mid \mathcal{D})& =\frac{p(\mathcal{D}\mid \mu )p(\mu )}{\int p(\mathcal{D}\mid \mu )p(\mu )d\mu }& =\alpha \prod _{k=1}^{n}p\left(x_k\mid \mu \right)p(\mu )\end{array}$$
• $\alpha$是个归一化常数
  $$\begin{array}{rl}p(\mu \mid \mathcal{D})& =\alpha \prod _{k=1}^n\stackrel{p\left(x_k\mid \mu \right)}{\overbrace{\frac{1}{\sqrt{2\pi }\sigma }\exp \left[-\frac{1}{2}{\left(\frac{x_k-\mu }{\sigma }\right)}^2\right]}}\stackrel{p(\mu )}{\overbrace{\frac{1}{\sqrt{2\pi }{\sigma }_0}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_0}{{\sigma }_0}\right)}^2\right]}}\\ & ={\alpha }^{\prime }\exp \left[-\frac{1}{2}\left(\sum _{k=1}^n{\left(\frac{\mu -x_k}{\sigma }\right)}^2+{\left(\frac{\mu -{\mu }_0}{{\sigma }_0}\right)}^2\right)\right]\\ & ={\alpha }^{\prime \prime }\exp \left[-\frac{1}{2}\left[\left(\frac{n}{{\sigma }^2}+\frac{1}{{\sigma }_0^2}\right){\mu }^2-2\left(\frac{1}{{\sigma }^2}\sum _{k=1}^n{x}_k+\frac{{\mu }_0}{{\sigma }_0^2}\right)\mu \right]\right]\\ & \end{array}$$
  $$p(\mu \mid \mathcal{D})=\frac{1}{\sqrt{2\pi }{\sigma }_n}\exp \left[-\frac{1}{2}{\left(\frac{\mu -{\mu }_n}{{\sigma }_n}\right)}^2\right]$$
  $${\sigma }_n^2=\frac{{\sigma }_0^2{\sigma }^2}{n{\sigma }_0^2+{\sigma }^2}⟶{\mu }_n=\left(\frac{n{\sigma }_0^2}{n{\sigma }_0^2+{\sigma }^2}\right){\hat{\mu }}_n+\frac{{\sigma }^2}{n{\sigma }_0^2+{\sigma }^2}{\mu }_0$$

贝叶斯估计一般情况

• 估计参数后验概率分布
  $$p(\mathbf{\theta }\mid \mathcal{D})=\frac{p(\mathcal{D}\mid \mathbf{\theta })p(\mathbf{\theta })}{\int p(\mathcal{D}\mid \mathbf{\theta })p(\mathbf{\theta })d\mathbf{\theta }}p(\mathcal{D}\mid \mathbf{\theta })=\prod _{k=1}^{n}p\left({\mathbf{x}}_k\mid \mathbf{\theta }\right)$$
• 估计数据概率分布
  $$p(\mathbf{x}\mid \mathcal{D})=\int p(\mathbf{x}\mid \mathbf{\theta })p(\mathbf{\theta }\mid \mathcal{D})d\mathbf{\theta }$$
  $$\text{ If }p(\theta \mid D)\text{ peaks at }\mathbf{\theta }=\hat{\mathbf{\theta }},p(\mathbf{x}\mid \mathrm{D})\text{ will be approximately }p(\mathbf{x}\mid \hat{\mathbf{\theta }})$$