个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题       【  http://t.csdnimg.cn/yUl2I   】
【C++】                  【  http://t.csdnimg.cn/6AbpV 】
数据结构与算法       【  http://t.csdnimg.cn/hKh2l  】

---

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

---

 全排列

题目链接：全排列

 题目

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

---

解法

题目解析

题目意思很简单，给我们一个数组，返回其 所有可能的全排列 

例如

输入：nums = [1,2,3]

输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

---

算法原理思路讲解    

1. 画出决策树（越详细越好）
2. 设计代码
   1. 设计全局变量
   2. 设计递归函数
3. 细节问题：回溯、剪枝、递归出口等问题（但是不是每个题都要）

 大家现在不懂也没关系，后面我会举例子，大家先知道有这三个步骤

---

一、画出决策树

决策树大概可以画成这样，首先在在 1，2，3 中选出一个，再继续向下选择

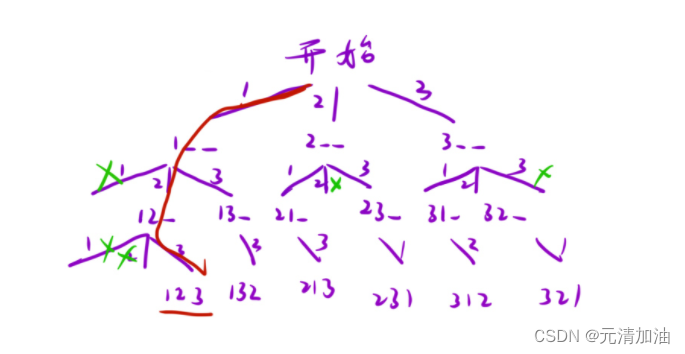
决策树就是我们后面设计函数的思路

---

二、设计代码

（1）全局变量

根据决策树的思路，首先我们要有一个二维数组存放排列的数（ret）,我们还需要一个路径变量（path）用来存放每个被选出来的数，最后我们还需要一个变量（check）用来判断这个数是否被选过了。

vector<vector<int>> ret;
vector<int> path;
bool check[10] = { false };

（2）设计递归函数

void dfs(vector<int>& nums);

---

三、细节问题：回溯、剪枝、递归出口 

回溯：我们只用再递归后，把 path 中数字删除，并在 check 中恢复成未被使用即可

递归出口 ：我们只用判断 path.size() == nums.size() ，如果相等，将 path 存入 ret 后，返回即可

现在思路就讲完了，大家可以自己做一做了

---

代码实现

• 时间复杂度：O(n×n!)，其中 n 为序列的长度
• 空间复杂度：O(n)，其中 n 为序列的长度。除答案数组以外，递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，这里可知递归调用深度为 O(n)

class Solution 
{
public:
    vector<vector<int>> ret;
    vector<int> path;
    bool check[10] = { false };

    void dfs(vector<int>& nums)
    {

	    if (path.size() == nums.size())
	    {
		    ret.push_back(path);
		    return;
	    }
	    for (int i = 0; i < nums.size(); i++)
	    {
		    if (!check[i])
		    {
			    check[i] = true;
			    path.push_back(nums[i]);
                dfs(nums);
                path.pop_back();   // 回溯
                check[i] = false;  // 回溯
            }
        }
    }

    vector<vector<int>> permute(vector<int>& nums) 
    {
        dfs(nums);
        return ret;
    }
};