差分法详解

news2024/9/24 21:27:06

前言
差分算法适用于一些需要对数组和序列进行增减、查询和更新操作的问题，可以提高计算效率和降低存储空间的需求。今天我将带大家学习如何使用差分法，会以例题来带大家使用差分法以增进理解。话不多说让我们开始吧！
在这里插入图片描述

文章目录

一维差分
尾声

一维差分

首先我们需要创建一个数组arr表示差分数组，然后再创建一个arrsum数组用来表示arr的前缀和。

即arr[i] = arrsum[i] - arrsum[i-1]
  arrsum[i] = arr[i] + arr[i-1] + ... + arr[1]

假设我们对arr数组进行操作从下标l到下标r中的每个元素都+1。如图
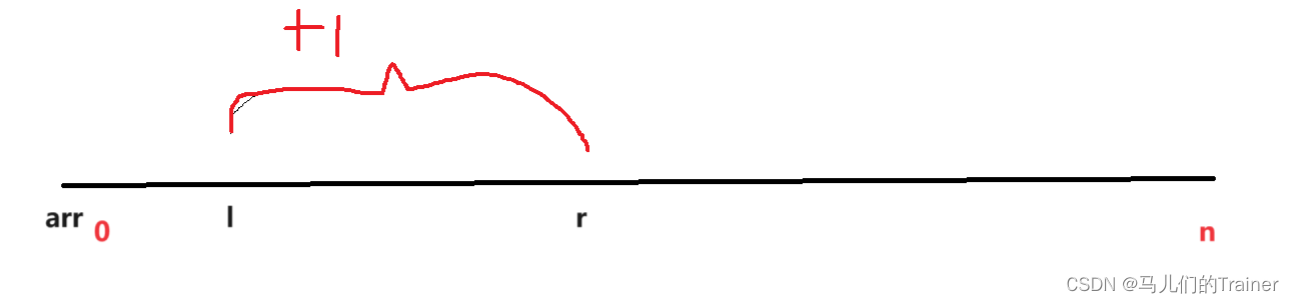
在这里插入图片描述
这里我们如果把l-r的每个元素都加1会十分的费事，但是我们如果对arrsum进行如下操作就会非常简单只需要让arrsum[ l ] + 1让arrsum[ r + 1 ] - 1即可。如图

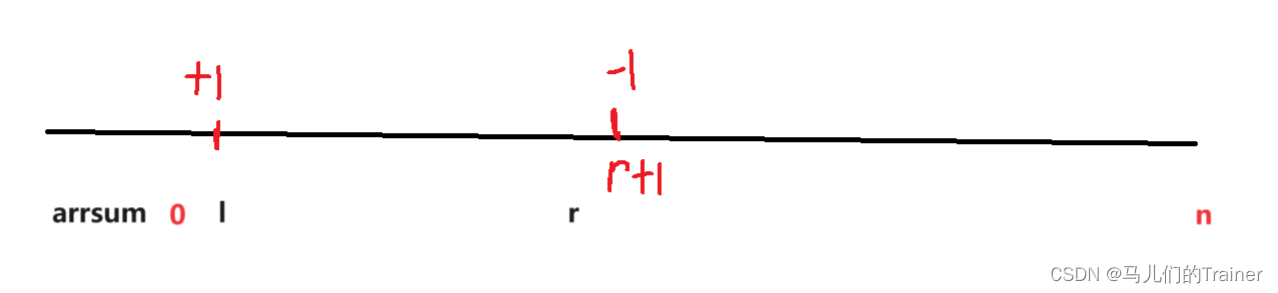
因为arrsum是前缀和，只要在l位置+1，r+1位置-1，l-r的群域内都进行了+1操作。
可是我们所求的数组并不是arrsum数组，那我们是不是可以想办法把arrsum变成arr呢？比如arr【5】里有 1 2 3 4 5 ，现在让arrsum的初始值设为 0， -1， -2， -3， --4。然后计算前缀和的时候用这个计算公式arrsum[ i ] = arrsum[ i ] + arrsum[ i -1] + arr[ i ]即可把arrsum变成操作后arr数组的模样，那么我们用这道题例题来带大家使用一下差分法。
给出数组arr，共有n个元素，对其进行q次操作，每次操作会对[ l , r ]区间内的元素+1，请输出进行操作后的arr数组。
输入样例
第一行为n和q
第二行为arr数组的元素
往后q行为l和r
10 2
1 2 3 4 5 6 7 8 9 10
1 5
9 10
输出样例
2 3 4 5 6 6 7 8 10 11
题解：

#include<stdio.h>
int main()
{
	int arr[100] = { 0 };
	int arrsum[100] = { 0 };//前缀和
	int n, q;
	scanf("%d %d", &n, &q);
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &arr[i]);
	}
	for (int i = 1; i <= n; i++)//使求出的前缀和数组刚好为操作后的arr数组
	{
		arrsum[i] += arr[i];
		arrsum[i + 1] -= arr[i];
	}
	while (q--)//q次操作
	{
		int l, r;
		scanf("%d %d", &l, &r);
		arrsum[l] += 1;
		arrsum[r + 1] -= 1;
	}
	for (int i = 2; i <= n; i++)//求前缀和（其实是造作后的arr数组）
	{
		arrsum[i] += arrsum[i - 1];
	}
	for (int i = 1; i <= n; i++)//打印出来
	{
		printf("%d ", arrsum[i]);
	}
	return 0;
}