算法的时间复杂度是什么？

时间复杂度的概念

时间复杂度是用来估算出程序的运行时间的。我们通常会估计算法的操作单元数量，来代表程序消耗的时间。

随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度，记为 O(f(n))。

大O的渐进表示法

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

推导大O阶的方法

1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项系数存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

O()括号里面的数表达的是这个算法的量级，大O是一个估算，并不是准确的执行次数。

大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。因为当n趋于无限大的时候，最高阶项系数对整体的效果影响不大。

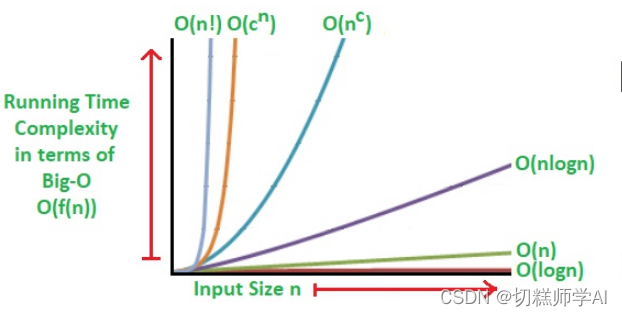
常见的时间复杂度等级

常见的时间复杂度等级有：O(1)(常数阶)，O(logn) (对数阶) ，O(n) (线性阶)，O(n^2) (平方阶) ，O(n^3) (立方阶)，O(2^n) (指数阶)。

他们的时间复杂度大小顺序依次为：

O(1) < O(logn) < O(n) < O(n^2) < O(n^3) < O(2^n)