线性回归在数据库中的应用

news2024/11/15 4:55:33

简介

今天看到微信群有人问，如何知道数据库一年的磁盘增量？如果没有研究过统计学，IT人员对于这个问题就只能靠经验了去断定了。没经验的往往都是回复扩容越大越好。当然未来的事情我们是无法预料的。本博主就通过简单的线性回归做一个计算，算出一年数据库的磁盘增量的大小和概率。

线性回归

线性回归是一种统计学和机器学习中常用的方法，用于建立自变量（输入）与因变量（输出）之间的线性关系模型。它假设自变量与因变量之间存在线性关系，并试图找到最佳拟合直线，以最小化预测值与实际观测值之间的差距。

在简单线性回归中，只涉及一个自变量和一个因变量。模型可以表示为：

y=mx+b

其中，y是因变量，x是自变量，m是斜率，b是截距。模型的目标是找到最合适的斜率和截距，使得预测值与实际观测值之间的平方差最小化，这被称为最小二乘法。

在多元线性回归中，涉及多个自变量和一个因变量。模型可以表示为：

其中，y是因变量，x1,x2,…,xn是多个自变量，b0,b1,b2,…,bn是回归系数。模型的目标是找到最合适的回归系数，以最小化预测值与实际观测值之间的误差。

线性回归常用于预测、建模和理解变量之间的关系。它的简单性和解释性使其成为许多数据分析和机器学习问题的基础。然而，线性回归也有其局限性，例如，它假设自变量与因变量之间的关系是线性的，而且对异常值敏感。

统计数据库大小

在实际生产中，我们需要知道数据库每日增量大小，具有一定的数据量进行对未来预测。我们使用存储过程，每天定时统计数据库大小。

创建表结构

用于装载数据库每日的磁盘空间大小和变化

CREATE TABLE daily_stats (
    date date NOT NULL,
	database_name varchar(200),
    databases_size integer NOT NULL,
    size_increment integer
);

创建存储过程计算数据库的磁盘空间大小和变化

CREATE OR REPLACE FUNCTION update_daily_stats()
RETURNS void AS $$
DECLARE
    today_size integer;
    yesterday_size integer;
    increment_size integer;
BEGIN
  
    -- 获取今天的数据库大小
    SELECT databases_size INTO yesterday_size
    FROM daily_stats
    WHERE date = current_date - interval '1 day';
   
   --插入到目标表中
   insert into  daily_stats (
    date,
	database_name,
    databases_size,
    size_increment)
SELECT
current_date, 
string_agg(datname::text,',') as database_name,
sum(pg_database_size(datname)) AS databases_size,
sum(pg_database_size(datname))-yesterday_size  size_increment
from pg_database;

    RETURN;
END;
$$ LANGUAGE plpgsql;

加入到定时调度中（这里使用crontab虚拟机自带的程序）

[postgres@vm03 ~]$ crontab -e 

0 0 * * *   psql  -c "SELECT update_daily_stats();"

让其统计每一天的数据库空间变化。

本文作为演示，假设出30天的数据库单日增量如下

30, 15, 64, 45, 92, 14, 23, 88, 14, 33, 24, 30, 14, 20, 36, 49, 16, 16, 32, 35, 46, 97, 13, 56, 32, 45, 26, 32, 65, 12

python编程

博主目前使用线性回归算法，多是numpy包和spark的MLlib库。本文均会进行举例说明。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 数据集
data = np.array([30, 15, 64, 45, 92, 14, 23, 88, 14, 33, 24, 30, 14, 20, 36, 49, 16, 16, 32, 35, 46, 97, 13, 56, 32, 45, 26, 32, 65, 12])

# 月份
months = np.arange(1, len(data) + 1)
##使用NumPy的arange函数生成一个包含1到数据集长度的数组，用于表示月份。


# 使用NumPy进行线性回归
coefficients = np.polyfit(months, data, 1)
linear_model = np.poly1d(coefficients)
##使用np.polyfit函数进行线性回归，其中1表示一次线性回归,次数越多，曲线的曲率越接近散点的波动。np.poly1d用于创建一个一次多项式对象，即线性模型。



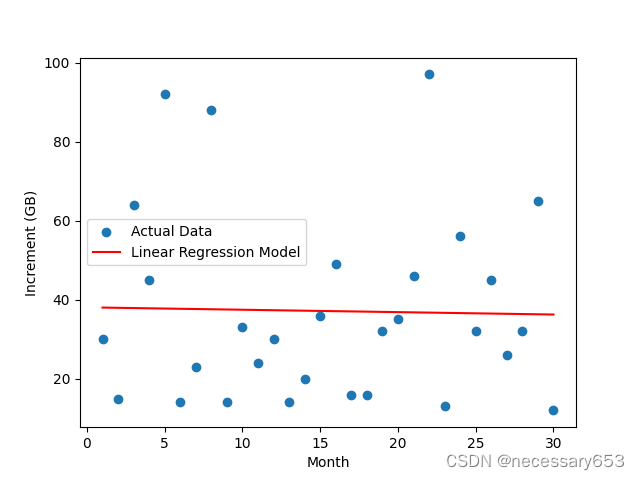
# 画出原始数据和线性回归模型的拟合结果
plt.scatter(months, data, label="Actual Data")
plt.plot(months, linear_model(months), color='red', label="Linear Regression Model")
plt.xlabel("Month")
plt.ylabel("Increment (GB)")
plt.legend()
plt.show()
##使用Matplotlib绘制散点图表示原始数据，然后使用红色线条表示线性回归模型的拟合结果。



# 预测一年的总增量
one_year_months = 12 * np.arange(1, 13)
one_year_increment = linear_model(one_year_months).sum()
print("预测一年的总增量：", one_year_increment)
##创建包含一年内每个月份的数组，然后使用线性回归模型预测每个月的增量，最后使用sum函数计算一年的总增量。


# 生成正态分布的随机样本
num_samples = 1000
simulated_data = np.random.normal(loc=one_year_increment, scale=5, size=num_samples)
#使用NumPy的random.normal函数生成一个包含1000个样本的正态分布，其中loc是均值，scale是标准差。

# 画出正态分布图
sns.histplot(simulated_data, kde=True, color='skyblue')
plt.axvline(x=one_year_increment, color='red', linestyle='--', label='Predicted Value')
plt.xlabel("One Year Increment")
plt.ylabel("Frequency")
plt.legend()
plt.show()
##使用Seaborn绘制正态分布的直方图和核密度估计图，同时用红色虚线表示预测值。

通过线性回归计算出在一个月内数据库空间增量大小的线性回归模型，