一、核函数 1

1. 多项式模型的局限性

在之前的学习中，了解到可以使用多项式模型来解决无法用直线进行分隔的分类问题。例如，对于判定边界的建模，可能会使用类似于以下形式的模型：

然而，这样的多项式模型在实际应用中可能存在一些问题，特别是对于高维度的数据。因此，需要一种更有效的方法来构造新的特征。

2. 核函数的引入

为了解决上述问题，引入了核函数的概念。核函数允许我们通过将原有特征与预先选定的地标（Landmarks）的近似程度来构造新的特征。具体而言，可以使用核函数计算新特征的值，例如高斯核函数（Gaussian Kernel）：

这里，表示实例 X 中所有特征与地标之间的距离的和。核函数的作用在于将实例的原有特征映射到一个新的空间，从而使得在这个新空间中的判定边界更为有效。

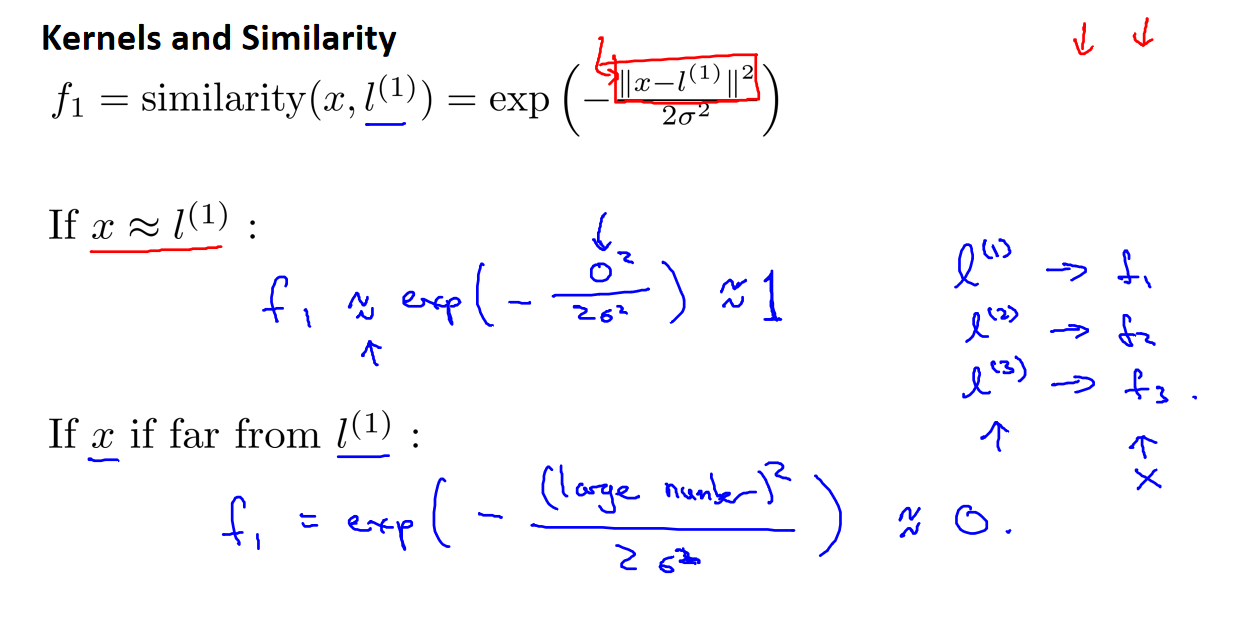
3. 核函数的效果

通过核函数，能够更灵活地构造新的特征，而不仅仅局限于原有特征的组合。核函数的选择影响了特征的映射效果，而合适的核函数能够在新的特征空间中更好地划分不同类别。

以高斯核函数为例，它的效果受到参数 σ 的控制。当实例与地标距离近时，新特征的值趋近于 1，而当距离较远时，新特征的值趋近于 0。这种灵活的特性使得支持向量机能够更好地适应不同数据集的特点。

在实际应用中，通过选取不同的地标和核函数，能够构建出更加复杂且适应性强的判定边界，从而提高模型的性能。核函数的引入使得支持向量机成为处理非线性分类问题的重要工具。

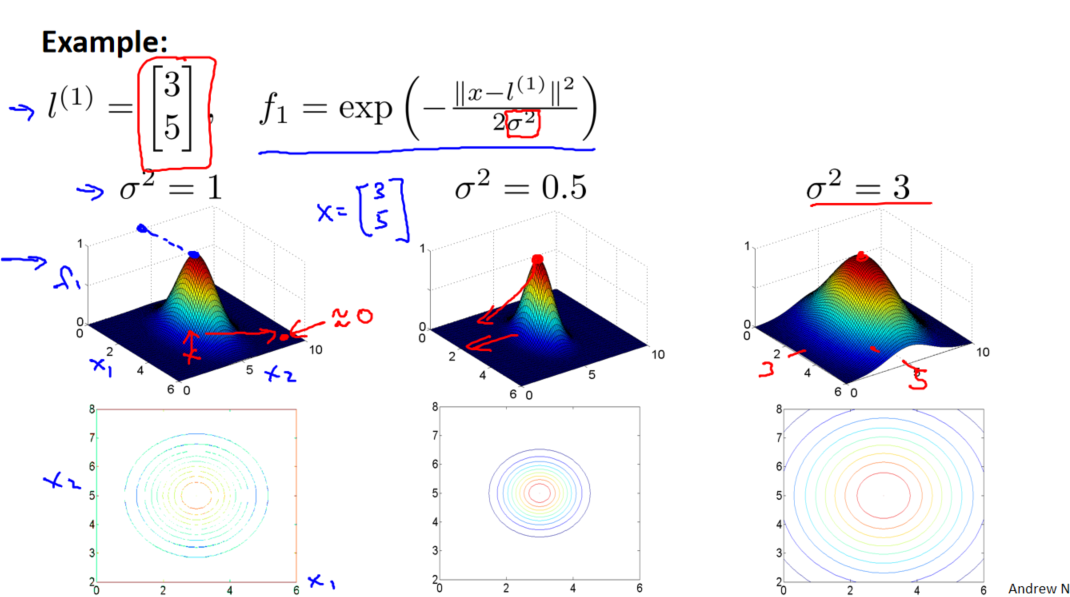
二、核函数 2

1. 地标的选择

选择地标是使用核函数的关键一步。通常情况下，会根据训练集的数量选择相同数量的地标。假设训练集中有 m 个实例，可以选择地标为 l(1)=x(1),l(2)=x(2),…,l(m)=x(m)。这样做的好处在于，新特征是基于原有特征与训练集中所有其他特征之间距离的基础上构建的。

2. 支持向量机假设的修改

引入核函数后，支持向量机的假设和代价函数都需要相应的修改。对于给定的实例 x，新特征 f 的计算方式如下：

支持向量机的假设变为：

预测 y=1 当 θ^Tf≥0，否则预测 y=0

相应地，代价函数也需要进行调整，其中对于正则化项的计算引入了一个矩阵 M，该矩阵取决于选择的核函数。

3. 参数调整

在实际应用中，需要根据数据集的特点来调整一些参数，其中两个关键参数是 C 和 σ。它们的影响如下：

• C：当 C 较大时，相当于 1/λ 较小，可能导致过拟合，高方差；C 较小时，相当于 1/λ 较大，可能导致低拟合，高偏差。

• σ：σ 较大时，可能导致低方差，高偏差；σ 较小时，可能导致低偏差，高方差。

在选择核函数时，特别是使用高斯核函数时，特征缩放是非常必要的。这有助于确保不同特征的尺度不会对核函数的计算产生不必要的影响。

最后，支持向量机也可以选择不使用核函数，即线性核函数。这在数据集特征较多而实例较少，或者不需要过于复杂的函数映射时是一种有效的选择。

参考资料：

[中英字幕]吴恩达机器学习系列课程

黄海广博士 - 吴恩达机器学习个人笔记