个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题       【  http://t.csdnimg.cn/yUl2I   】
【C++】                  【  http://t.csdnimg.cn/6AbpV 】
数据结构与算法       【  http://t.csdnimg.cn/hKh2l  】

---

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

---

二叉树的所有路径

题目链接：二叉树的所有路径

题目

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

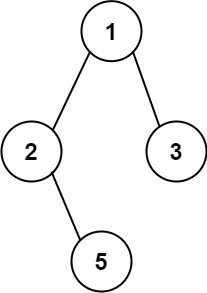
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 10

---

解法

题目解析

题目意思很简单，给我们一颗二叉树，让我们返回二叉树所有的路径

例如：

输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

---

算法原理思路讲解   

1. 如果当前节点不为空，就将当前节点的值加⼊路径 path 中，否则直接返回；
2. 判断当前节点是否为叶⼦节点，如果是，则将当前路径加⼊到所有路径的存储数组 ret 中；
3. 否则，将当前节点值加上 "->" 作为路径的分隔符，继续递归遍历当前节点的左右⼦节点。

---

 代码实现 

• 时间复杂度：O(N^2)，其中 N 表示节点数目。在深度优先搜索中每个节点会被访问一次且只会被访问一次，每一次会对 path 变量进行拷贝构造，时间代价为 O(N)，故时间复杂度为 O(N^2)。
• 空间复杂度：O(N^2)，其中 N 表示节点数目。除答案数组外我们需要考虑递归调用的栈空间。在最坏情况下，当二叉树中每个节点只有一个孩子节点时，即整棵二叉树呈一个链状，此时递归的层数为 NNN.

  /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
   *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
   *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
   * };
   */
  class Solution 
  {
  public:
      vector<string> ret;
  
      void dfs(TreeNode* root , string path)
      {
          if (root != nullptr)
              path += to_string(root->val);
          else
              return ;
          
          if(root->left == nullptr && root->right == nullptr)
          {
              ret.push_back(path);
              return;
          }
          path += "->";
          if(root->left) dfs(root->left, path);
          if(root->right) dfs(root->right, path);
      }
  
      vector<string> binaryTreePaths(TreeNode* root) 
      {
          string path;
          if(root == nullptr) 
              return ret;
  
          dfs(root,path);
          return ret;
      }
  };