1.题目

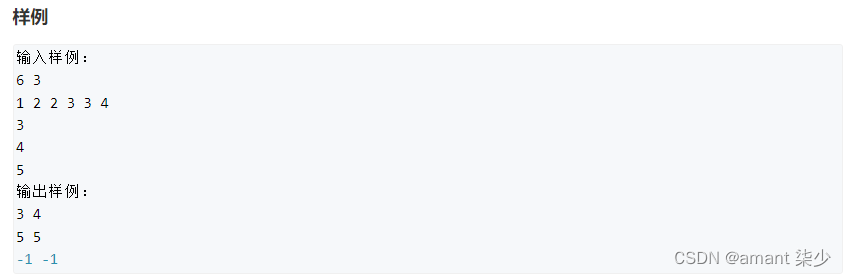
给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。
对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。
如果数组中不存在该元素，则返回“-1 -1”。
输入格式
第一行包含整数n和q，表示数组长度和询问个数。
第二行包含n个整数（均在1~10000范围内），表示完整数组。
接下来q行，每行包含一个整数k，表示一个询问元素。
输出格式
共q行，每行包含两个整数，表示所求元素的起始位置和终止位置。
如果数组中不存在该元素，则返回“-1 -1”。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000

2.基本思想

二分

整数二分步骤：
1.找一个区间[L，R]，使得答案一定在该区间中
2.找一个判断条件，使得该判断条件具有二段性，并且答案一定是该二段性的分界点。
3.分析终点M在该判断条件下是否成立，如果成立，考虑答案在哪个区间；如果不成立，考虑答案在哪个区间；
4.如果更新方式写的是R=Mid，则不用做任何处理；如果更新方式写的是L=Mid，则需要在计算Mid时加上1。

3.代码实现

import java.io.IOException;
import java.util.Scanner;

public class _789数的范围 {
    static int[] arr = new int[100010];

    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        //获取输入
        int n = sc.nextInt();
        int q = sc.nextInt();
        for (int i = 0; i < n; i++)
            arr[i] = sc.nextInt();

        //依次查询 q个数字
        for (int i = 0; i < q; i++) {
            int x = sc.nextInt();
            //二分x的左端点
            int l = 0, r = n - 1;
            while (l < r) {
                int mid = l + r >> 1;
                if (arr[mid] >= x) r = mid;
                else l = mid + 1;
            }
            //判断得到的第一个数字 是否等于 查询的 x
            if (arr[r] == x) {
                System.out.print(r+" ");
                r = n - 1;
                while (l < r) {
                    int mid = l + r +1>> 1;// +1
                    if (arr[mid] <= x) l = mid;
                    else r = mid - 1;
                }
                System.out.print(l);
            } else
                System.out.println("-1 -1");
        }
    }
}

4.总结

整数二分模板

模板一

// 区间[l, r]被划分成 [l, mid] 和 [mid+1, r]时使用
int bsearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check[mid)  // check() 判断 mid是否满足性质
            r = mid; 
        else
            l = mid + 1;
    }
    return l;
}

模板二

// 区间[l, r]被划分成 [l, mid-1] 和 [mid, r]时使用
int bsearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;   // 注意
        if (check[mid)  // check() 判断 mid是否满足性质
            l = mid;
        else
            r = mid - 1;//有减 必有加

    }
    return l;
}