【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码)
- 基本概念
- 确定性时间序列分析方法
- 平稳时间序列模型
- ARIMA模型
- 季节性序列
- 习题8.1
- 1. 题目要求
- 2.解题过程
- 3.程序
- 4.结果
- 习题8.2
- 1. 题目要求
- 2.解题过程
- 3.程序
- 4.结果
- 习题8.3
- 1. 题目要求
- 2.解题过程
- 3.程序
- 4.结果
本系列侧重于例题实战与讲解,希望能够在例题中理解相应技巧。文章开头相关基础知识只是进行简单回顾,读者可以搭配课本或其他博客了解相应章节,然后进入本文例题实战,效果更佳。
如果这篇文章对你有帮助,欢迎点赞与收藏~

基本概念
时间序列预测是一种预测方法,它通过将观察对象按照时间顺序排列,构成一个所谓的“时间序列”。通过分析这些时间序列过去的变化规律,可以推断未来的可能变化、趋势和规律。这种方法实际上是一种回归模型,其基本原理有两个方面:一是承认事物发展的延续性,即通过分析过去时间序列的数据来预测事物的发展趋势;二是考虑到偶然因素的影响所带来的随机性。为了减少随机波动的影响,需要利用历史数据进行统计分析,并对数据进行适当处理以进行趋势预测。
时间序列预测法的优点在于其简单易行,易于掌握,能够充分利用原时间序列的数据,计算速度快,并且对模型参数具有动态确定的能力。此外,精度较高,特别是当采用组合时间序列或将时间序列与其他模型组合时,其效果更佳。然而,这种方法也有其局限性,主要是不能反映事物的内在联系,无法分析两个因素之间的相关关系,更适用于短期而非长期预测。
时间序列预测法在各个领域都有广泛的应用,如在金融市场分析、气象预测、工业生产和库存管理等领域。在实际应用中,时间序列预测通常涉及到多种技术和方法,如移动平均、指数平滑法、季节性调整、自回归移动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。这些技术各有特点,适用于不同类型的数据和不同的预测需求。
确定性时间序列分析方法
确定性时间序列分析主要关注那些展现出一定规律或模式的时间序列数据,这些规律通常可以用一组固定的数学函数来描述。这种分析方法试图从时间序列数据中识别出趋势、周期性或季节性等成分。确定性时间序列的主要特点是,一旦识别出其规律,就可以准确预测未来的值。典型的确定性时间序列分析方法包括趋势线分析、季节性分解等。
平稳时间序列模型
平稳时间序列模型是指那些其统计特性(如均值、方差等)随时间推移保持不变的时间序列。在平稳序列中,时间序列的行为不会因时间的改变而发生变化,这使得模型预测变得更加简单和准确。平稳性是很多时间序列模型,如自回归(AR)模型、移动平均(MA)模型、和自回归移动平均(ARMA)模型的重要前提。
ARIMA模型
ARIMA(自回归积分滑动平均)模型是时间序列预测中最常用的方法之一。它结合了自回归(AR)和移动平均(MA)模型,并加入了差分的概念,用以将非平稳时间序列转换为平稳时间序列。ARIMA模型由三个主要参数构成:自回归项(AR)、差分阶数(I,积分)、和移动平均项(MA)。这种模型特别适合处理呈现长期趋势或季节性的非平稳时间序列。
季节性序列
季节性序列指的是那些展现出明显季节性模式的时间序列,即数据在固定时间间隔内呈现出重复模式。这种序列通常与特定季节或周期性事件相关,如月销售量、每日温度变化等。季节性时间序列分析的目的是识别并建模这种周期性模式,以准确预测未来周期内的数值。处理季节性时间序列的常用方法包括季节性分解和季节性ARIMA(SARIMA)模型,后者专门用来处理同时包含季节性和非季节性成分的时间序列。
习题8.1
1. 题目要求


2.解题过程
解:
(1)
由N=3,我们可以取预测公式:
M
t
+
1
=
y
t
+
y
t
−
1
+
y
t
−
2
3
,
t
=
3
,
4
,
.
.
.
,
11
M_{t+1}=\frac{y_t+y_{t-1}+y_{t-2}}{3},\ t=3,4,...,11
Mt+1=3yt+yt−1+yt−2, t=3,4,...,11
其中
M
9
=
133.0
,
M
10
=
136.8
,
M
11
=
137.5
M_9=133.0,M_{10}=136.8,M_{11}=137.5
M9=133.0,M10=136.8,M11=137.5 为预测值。
预测的标准误差为:
S
=
∑
t
=
4
8
(
M
t
−
y
t
)
2
5
=
19.3542
S=\sqrt{\frac{\sum_{t=4}^{8}(M_t-y_t)^2}{5}}=19.3542
S=5∑t=48(Mt−yt)2=19.3542
(2)
二次指数平滑法的公式:
{
S
t
(
1
)
=
α
y
t
+
(
1
−
α
)
S
t
−
1
(
1
)
S
t
(
1
)
=
α
S
t
(
1
)
+
(
1
−
α
)
S
t
−
1
(
2
)
\begin{align*} \begin{cases} S_t^{(1)}=\alpha y_t+(1-\alpha)S_{t-1}^{(1)}\\ S_t^{(1)}=\alpha S_t^{(1)}+(1-\alpha)S_{t-1}^{(2)} \end{cases} \end{align*}
{St(1)=αyt+(1−α)St−1(1)St(1)=αSt(1)+(1−α)St−1(2)
其中
S
t
(
1
)
S_t^{(1)}
St(1)为一次指数平滑值,
S
t
(
2
)
S_t^{(2)}
St(2)为二次指数平滑值。
当时间序列开始具有直线趋势时,建立直线指数平滑预测模型:
y
^
t
+
m
=
a
t
+
b
t
m
{
a
t
=
2
S
t
(
1
)
−
S
t
(
2
)
b
t
=
α
1
−
α
(
S
t
(
1
)
−
S
t
(
2
)
)
\begin{align*} &\hat{y}_{t+m}=a_t+b_tm\\ &\begin{cases} a_t=2S_t^{(1)}-S_t^{(2)}\\ b_t=\frac{\alpha}{1-\alpha}(S_t^{(1)}-S_t^{(2)}) \end{cases} \end{align*}
y^t+m=at+btm{at=2St(1)−St(2)bt=1−αα(St(1)−St(2))
在
α
=
0.3
\alpha=0.3
α=0.3 时,预测的标准误差是:
S
=
∑
t
=
1
8
(
y
^
t
−
y
t
)
2
7
=
11.7966
S=\sqrt{\frac{\sum_{t=1}^{8}(\hat{y}_t-y_t)^2}{7}} = 11.7966
S=7∑t=18(y^t−yt)2=11.7966
在
α
=
0.6
\alpha=0.6
α=0.6 时,预测的标准误差是:
S
=
∑
t
=
1
8
(
y
^
t
−
y
t
)
2
7
=
7.0136
S=\sqrt{\frac{\sum_{t=1}^{8}(\hat{y}_t-y_t)^2}{7}} = 7.0136
S=7∑t=18(y^t−yt)2=7.0136
(3)
从上面两小问的计算过程来看,选取标准误差最小的,也即 α = 0.6 \alpha=0.6 α=0.6 时的二次指数平滑模型
(4)
按照第三问的结果,取二次指数平滑模型的预测结果即可(计算过程见后文)。
α = 0.6 \alpha=0.6 α=0.6时,1982年的产量预测值为152.9457亿米;1985年的产量预测为182.8640亿米
3.程序
(1)
求解的MATLAB程序如下:
clc, clear
yt = [80.8, 94.0, 88.4, 101.5, 110.3, 121.5, 134.7, 142.7];
m = length(yt);
n = 3; % 定义了移动平均窗口的大小
for i = n + 1:m + 1
% 在循环内部,用移动平均法计算 ythat 向量的当前元素值,即取窗口内最近的 n 个元素的平均值
ythat(i) = sum(yt(i-n:i-1)) / n;
end
ythat
for i = m + 1:m + n
yt(i) = ythat(i);
ythat(i+1) = sum(yt(i-n+1:i)) / n;
end
% 将 yhat 设置为 ythat 的最后四个元素
yhat = ythat(end-3:end)
% 计算原始数据 yt 和平滑后的数据 ythat 的标准差 s1
% 这里只计算从第 n+1 个元素到最后一个元素的标准差,因为前 n 个元素无法进行平滑处理
% sqrt 和 mean 分别计算标准差的平方和的平均值和标准差本身
s1 = sqrt(mean((yt(n+1:m) - ythat(n+1:m)).^2))
(2)
求解的MATLAB程序如下:(0.3和0.6都尝试一次,仅修改该数据即可)
clc, clear
yt = [80.8, 94.0, 88.4, 101.5, 110.3, 121.5, 134.7, 142.7];
n = length(yt);
% 两个平滑值
% 这里使用了简单平均法来计算 st1(1),即前三个数据点的平均值,并将其赋给 st1(1) 和 st2(1)
st1(1) = mean(yt(1:3));
st2(1) = st1(1);
% 平滑系数
alpha = 0.3;
% 循环从 i=2 开始,因为 st1(1) 和 st2(1) 已经在前面初始化了
for i = 2:n
% 使用指数平滑法更新 st1(i) 和 st2(i)
% st1(i) 的更新使用的是单次指数平滑法,而 st2(i) 的更新使用的是二次指数平滑法
st1(i) = alpha * yt(i) + (1 - alpha) * st1(i-1);
st2(i) = alpha * st1(i) + (1 - alpha) * st2(i-1);
end
% 计算趋势系数 at 和 bt
at = 2 * st1 - st2;
bt = alpha / (1 - alpha) * (st1 - st2);
% 计算预测值 yhat
yhat = at + bt;
sigma = sqrt(mean((yt(2:end) - yhat(1:end-1)).^2));
% 根据模型预测最后一个数据点后的趋势,进一步预测接下来四个数据点的值
m = 1:4;
yhat2 = at(end) + bt(end) * m;
sigma
yhat2
4.结果
(1)

(2)
在 α = 0.3 \alpha=0.3 α=0.3 时

在 α = 0.6 \alpha=0.6 α=0.6 时

(3)
选取标准误差最小的,也即 α = 0.6 \alpha=0.6 α=0.6 时的二次指数平滑模型
(4)
最终结果:1982年的产量预测值为152.9457亿米;1985年的产量预测为182.8640亿米
习题8.2
1. 题目要求
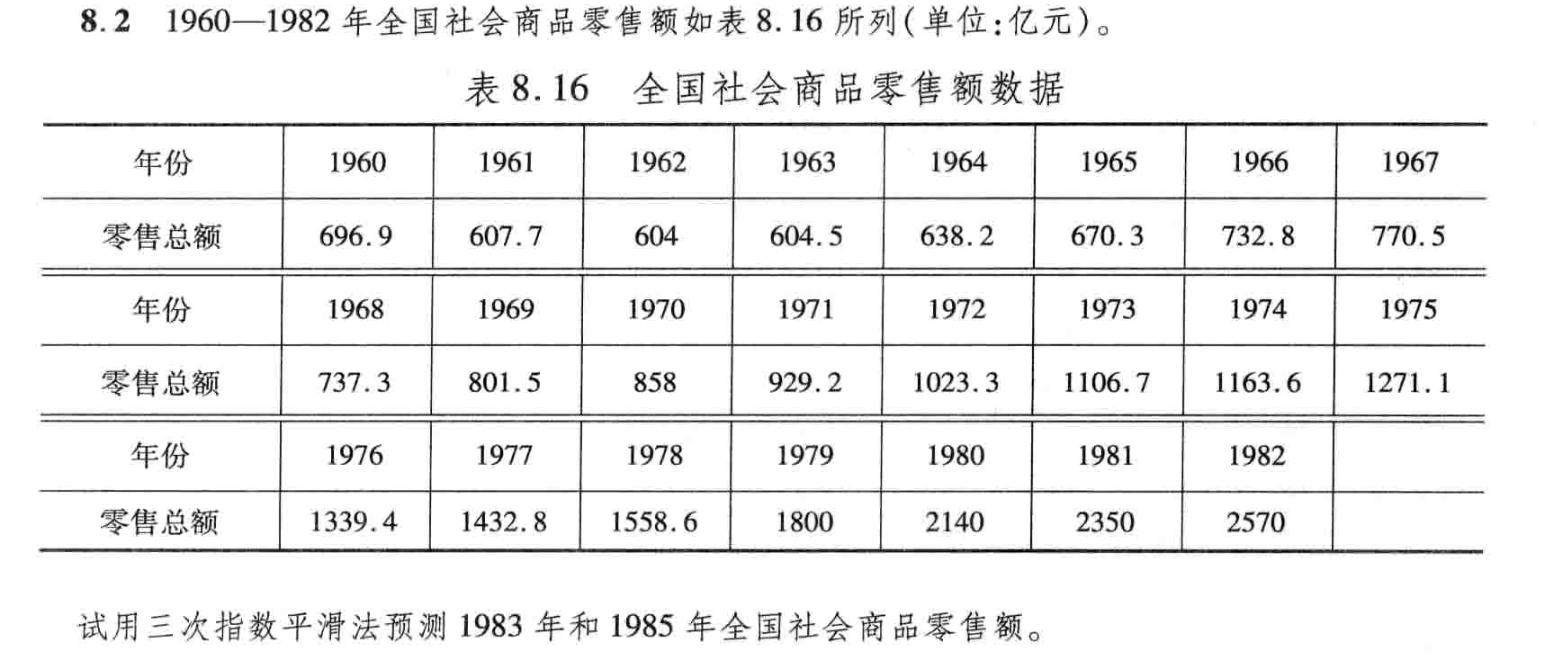
2.解题过程
解:
计算公式为:
{
S
t
(
1
)
=
α
y
t
+
(
1
−
α
)
S
t
−
1
(
1
)
S
t
(
2
)
=
α
S
t
(
1
)
+
(
1
−
α
)
S
t
−
1
(
2
)
S
t
(
3
)
=
α
S
t
(
2
)
+
(
1
−
α
)
S
t
−
1
(
3
)
\begin{align*} \begin{cases} S_t^{(1)}=\alpha y_t+(1-\alpha)S_{t-1}^{(1)}\\ S_t^{(2)}=\alpha S_t^{(1)}+(1-\alpha)S_{t-1}^{(2)}\\ S_t^{(3)}=\alpha S_t^{(2)}+(1-\alpha)S_{t-1}^{(3)} \end{cases} \end{align*}
⎩
⎨
⎧St(1)=αyt+(1−α)St−1(1)St(2)=αSt(1)+(1−α)St−1(2)St(3)=αSt(2)+(1−α)St−1(3)
其中
S
t
(
1
)
,
S
t
(
2
)
,
S
t
(
3
)
S_t^{(1)},S_t^{(2)},S_t^{(3)}
St(1),St(2),St(3) 分别是一、二、三次指数平滑值。
初始值计算如下:
S
0
(
1
)
=
S
0
(
2
)
=
S
0
(
3
)
=
y
1
+
y
2
+
y
3
3
=
636.2
S_0^{(1)}=S_0^{(2)}=S_0^{(3)}=\frac{y_1+y_2+y_3}{3}=636.2
S0(1)=S0(2)=S0(3)=3y1+y2+y3=636.2
预测模型为:
y
^
t
+
m
=
a
t
+
b
t
m
+
c
t
m
2
,
m
=
1
,
2
,
.
.
.
\hat{y}_{t+m}=a_t+b_tm+c_tm^2,m=1,2,...
y^t+m=at+btm+ctm2,m=1,2,...
{ a t = 3 S t ( 1 ) − 3 S t ( 2 ) + S t ( 3 ) b t = α 2 ( 1 − α ) 2 [ ( 6 − 5 α ) S t ( 1 ) − 2 ( 5 − 4 α ) S t ( 2 ) + ( 4 − 3 α ) S t ( 3 ) ] c t = α 2 2 ( 1 − α ) 2 [ S t ( 1 ) − 2 S t ( 2 ) + S t ( 3 ) ] \begin{align*} \begin{cases} a_t=3S_t{(1)}-3S_t{(2)}+S_t{(3)}\\ b_t=\frac{\alpha}{2(1-\alpha)^2}[(6-5\alpha)S_t^{(1)}-2(5-4\alpha)S_t{(2)}+(4-3\alpha)S_t{(3)}]\\ c_t=\frac{\alpha^2}{2(1-\alpha)^2}[S_t^{(1)}-2S_t^{(2)}+S_t^{(3)}] \end{cases} \end{align*} ⎩ ⎨ ⎧at=3St(1)−3St(2)+St(3)bt=2(1−α)2α[(6−5α)St(1)−2(5−4α)St(2)+(4−3α)St(3)]ct=2(1−α)2α2[St(1)−2St(2)+St(3)]
t=23时,计算结果如下:
a
23
=
2572.2613
,
b
23
=
259.3374
,
c
23
=
8.9819
a_{23}=2572.2613,b_{23}=259.3374,c_{23}=8.9819
a23=2572.2613,b23=259.3374,c23=8.9819
y ^ 23 + m = 8.9819 m 2 + 259.3373 m + 2572.2612 \hat{y}_{23+m}=8.9819m^2+259.3373m+2572.2612 y^23+m=8.9819m2+259.3373m+2572.2612
最终求得:1983、1985年的预测值分别为 2840.58058505076 亿元,3431.11062220508 亿元
3.程序
求解的MATLAB程序如下:
clc, clear
% yt记录零售总额数据
yt = [696.9, 607.7, 604, 604.5, 638.2, 670.3, 732.8, 770.5, ...
737.3, 801.5, 858, 929.2, 1023.3, 1106.7, 1163.6, 1271.1, ...
1339.4, 1432.8, 1558.6, 1800, 2140, 2350, 2570]';
n = length(yt);
alpha = 0.3; % 意味着对于当前时刻的预测,历史数据的权重为 0.7,预测数据的权重为 0.3
st0 = mean(yt(1:3)); % 计算数据向量中前三个数据的平均值,并将其设置为初始平滑值st0
% 计算三次指数平滑法中的一阶平滑值st1、二阶平滑值st2和三阶平滑值st3的初始值
st1(1) = alpha * yt(1) + (1 - alpha) * st0;
st2(1) = alpha * st1(1) + (1 - alpha) * st0;
st3(1) = alpha * st2(1) + (1 - alpha) * st0;
% 使用循环计算每个时刻的一阶平滑值st1、二阶平滑值st2和三阶平滑值st3
for i = 2:n
st1(i) = alpha * yt(i) + (1 - alpha) * st1(i-1);
st2(i) = alpha * st1(i) + (1 - alpha) * st2(i-1);
st3(i) = alpha * st2(i) + (1 - alpha) * st3(i-1);
end
% 根据三次指数平滑法的公式,计算出平滑后的数据yhat、趋势项系数bt和季节项系数ct
at = 3 * st1 - 3 * st2 + st3;
bt = 0.5 * alpha / (1 - alpha)^2 * ...
((6 - 5 * alpha) * st1 - 2 * (5 - 4 * alpha) * st2 + (4 - 3 * alpha) * st3);
ct = 0.5 * alpha^2 / (1 - alpha)^2 * ...
(st1 - 2 * st2 + st3);
yhat = at + bt + ct;
xishu = [ct(end), bt(end), at(end)]
yuce = polyval(xishu, [1:3]) % 计算未来三年的预测值
4.结果
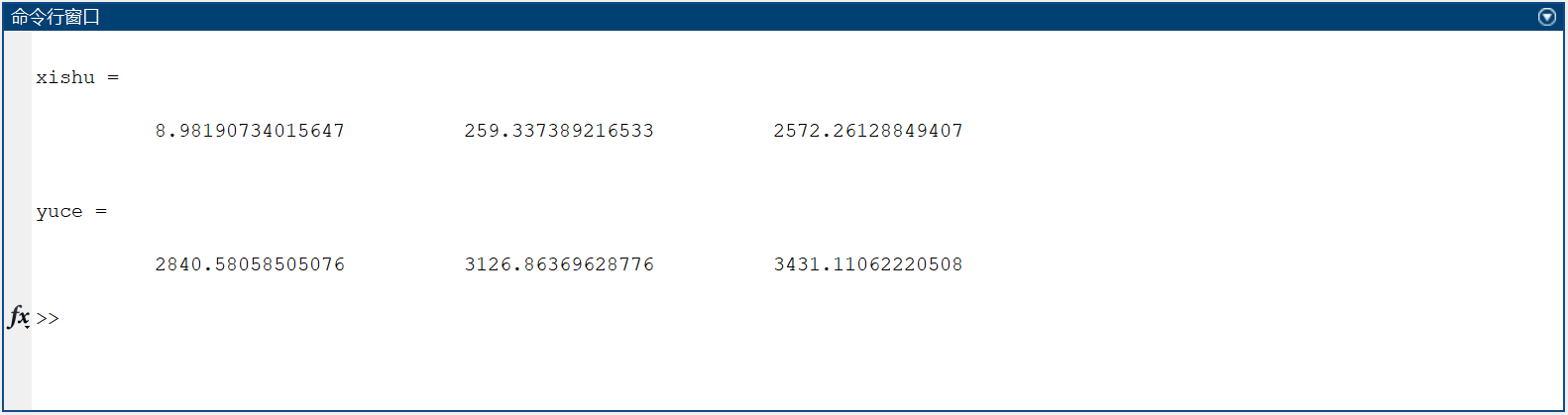
1983、1985年的预测值分别为 2840.58058505076 亿元,3431.11062220508 亿元
习题8.3
1. 题目要求

2.解题过程
解:
本题我选取了两个曲线。
(1)Compertz曲线
一般形式为:
y
^
t
=
K
a
b
t
,
K
>
0
,
0
<
a
≠
1
,
0
<
b
≠
1
\hat{y}_t=Ka^{b^t},K>0,0<a\neq1,0<b\neq1
y^t=Kabt,K>0,0<a=1,0<b=1
两边取对数
ln
y
^
t
=
ln
K
+
b
t
ln
a
\ln\hat{y}_t=\ln K+b^t\ln a
lny^t=lnK+btlna
记
y
^
t
′
=
ln
y
^
,
K
′
=
ln
K
,
a
′
=
ln
a
\hat{y}'_t = \ln\hat{y},K'=\ln K,a'=\ln a
y^t′=lny^,K′=lnK,a′=lna
则
y
^
t
′
=
K
′
+
a
′
b
t
\hat{y}'_t=K'+a'b^t
y^t′=K′+a′bt
三和法估计参数:
S
1
=
∑
t
=
1
m
y
t
′
,
S
1
=
∑
t
=
m
+
1
2
m
y
t
′
,
S
1
=
∑
t
=
2
m
+
1
3
m
y
t
′
S_1=\sum_{t=1}^{m}y'_t,S_1=\sum_{t=m+1}^{2m}y'_t,S_1=\sum_{t=2m+1}^{3m}y'_t
S1=t=1∑myt′,S1=t=m+1∑2myt′,S1=t=2m+1∑3myt′
则
{
b
=
(
S
3
−
S
2
S
2
−
S
1
)
1
m
a
′
=
(
S
2
−
S
1
)
b
−
1
b
(
b
m
−
1
)
2
K
′
=
1
m
[
S
1
−
a
′
b
(
b
m
−
1
)
b
−
1
]
\begin{align*} \begin{cases} b&=(\frac{S_3-S_2}{S_2-S_1})^{\frac{1}{m}}\\ a'&=(S_2-S_1)\frac{b-1}{b(b^m-1)^2}\\ K'&=\frac{1}{m}[S_1-\frac{a'b(b^m-1)}{b-1}] \end{cases} \end{align*}
⎩
⎨
⎧ba′K′=(S2−S1S3−S2)m1=(S2−S1)b(bm−1)2b−1=m1[S1−b−1a′b(bm−1)]
解得
b
=
0.8244
,
a
′
=
−
1.7075
,
a
=
0.1813
,
K
′
=
2.5804
,
K
=
13.2021
b=0.8244,a'=-1.7075,a=0.1813,K'=2.5804,K=13.2021
b=0.8244,a′=−1.7075,a=0.1813,K′=2.5804,K=13.2021
所以Comperz曲线方程为:
y
^
t
=
13.2021
×
0.181
3
0.824
4
t
\hat{y}_t=13.2021\times 0.1813^{0.8244^t}
y^t=13.2021×0.18130.8244t
1985年,1990年的粮食产量分别为12.3830,12.8840
(2)Logistic曲线
一般形式为:
d
y
d
x
=
r
y
(
1
−
y
L
)
\frac{d y}{d x}=ry(1-\frac{y}{L})
dxdy=ry(1−Ly)
解此微分方程:
y
=
L
1
+
c
e
−
r
t
y=\frac{L}{1+ce^{-rt}}
y=1+ce−rtL
记Logistic曲线一般形式为:
y
t
=
1
K
+
a
b
t
,
K
>
0
,
a
>
0
,
0
<
b
≠
1
y_t=\frac{1}{K+ab^t},K>0,a>0,0<b\neq1
yt=K+abt1,K>0,a>0,0<b=1
令
y
t
′
=
1
y
t
y'_t=\frac{1}{y_t}
yt′=yt1 得:
y
t
′
=
K
+
a
b
t
y'_t=K+ab^t
yt′=K+abt
三和法估计参数:
S
1
=
∑
t
=
1
m
y
t
′
,
S
1
=
∑
t
=
m
+
1
2
m
y
t
′
,
S
1
=
∑
t
=
2
m
+
1
3
m
y
t
′
S_1=\sum_{t=1}^{m}y'_t,S_1=\sum_{t=m+1}^{2m}y'_t,S_1=\sum_{t=2m+1}^{3m}y'_t
S1=t=1∑myt′,S1=t=m+1∑2myt′,S1=t=2m+1∑3myt′
则
{
b
=
(
S
3
−
S
2
S
2
−
S
1
)
1
m
a
=
(
S
2
−
S
1
)
b
−
1
b
(
b
m
−
1
)
2
K
=
1
m
[
S
1
−
a
′
b
(
b
m
−
1
)
b
−
1
]
\begin{align*} \begin{cases} b=(\frac{S_3-S_2}{S_2-S_1})^{\frac{1}{m}}\\ a=(S_2-S_1)\frac{b-1}{b(b^m-1)^2}\\ K=\frac{1}{m}[S_1-\frac{a'b(b^m-1)}{b-1}] \end{cases} \end{align*}
⎩
⎨
⎧b=(S2−S1S3−S2)m1a=(S2−S1)b(bm−1)2b−1K=m1[S1−b−1a′b(bm−1)]
解得
b
=
0.7501
,
a
=
0.2796
,
K
=
0.0805
b=0.7501,a=0.2796,K=0.0805
b=0.7501,a=0.2796,K=0.0805
所以Logistic曲线方程为:
y
^
t
=
1
0.0805
+
0.2796
×
0.750
1
t
\hat{y}_t=\frac{1}{0.0805+0.2796\times0.7501^t}
y^t=0.0805+0.2796×0.7501t1
1985年,1990年的粮食产量分别为12.1068,12.3467
3.程序
(1)
求解的MATLAB程序如下:
clc, clear
y = [3.78, 4.19, 4.83, 5.46, 6.71, 7.99, 8.60, 9.24, ...
9.67, 9.87, 10.49, 10.92, 10.93, 12.39, 12.59];
yt = log(y); % 将y取自然对数,以便进行Compertz曲线拟合
n = length(yt);
m = n / 3;
% 计算yt的长度n和m,m是将时间分成三段后的长度
% Compertz曲线需要将时间分成三个等长的部分
% 计算yt的前1/3、中间1/3和后1/3的和
s1 = sum(yt(1:m));
s2 = sum(yt(m+1:2*m));
s3 = sum(yt(2*m+1:3*m));
b = ((s3 - s2) / (s2 - s1))^(1 / m); % b控制曲线的形状
a = (s2 - s1) * (b - 1) / (b * (b^m - 1)^2); % a控制曲线的位置
k = (s1 - a * b * (b^m - 1) / (b - 1)) / m; % k是拟合曲线的最小值
a = exp(a);
k = exp(k); % 对a和k值进行指数运算,以将其还原为实际值
yuce = @(t) k * a.^(b.^t); % 创建一个匿名函数
ypre = yuce([n + 2, n + 7])
(2)
求解的MATLAB程序如下:
clc, clear
y = [3.78, 4.19, 4.83, 5.46, 6.71, 7.99, 8.60, 9.24, ...
9.67, 9.87, 10.49, 10.92, 10.93, 12.39, 12.59];
yt = 1 ./ y;
% yt向量的长度n和分成三组时每组的长度m
n = length(yt);
m = n / 3;
% 每组的元素之和
s1 = sum(yt(1:m));
s2 = sum(yt(m+1:2*m));
s3 = sum(yt(2*m+1:3*m));
% 使用Logistic曲线拟合yt向量。变量b是增长率,变量a是曲线的形状,变量k是曲线的位置
b = ((s3 - s2) / (s2 - s1))^(1 / m);
a = (s2 - s1) * (b - 1) / (b * (b^m - 1)^2);
k = (s1 - a * b * (b^m - 1) / (b - 1)) / m;
yuce = @(t) 1 ./ (k + a * b.^t);
ypre = yuce([n + 2, n + 7])
4.结果

如果这篇文章对你有帮助,欢迎点赞与收藏~