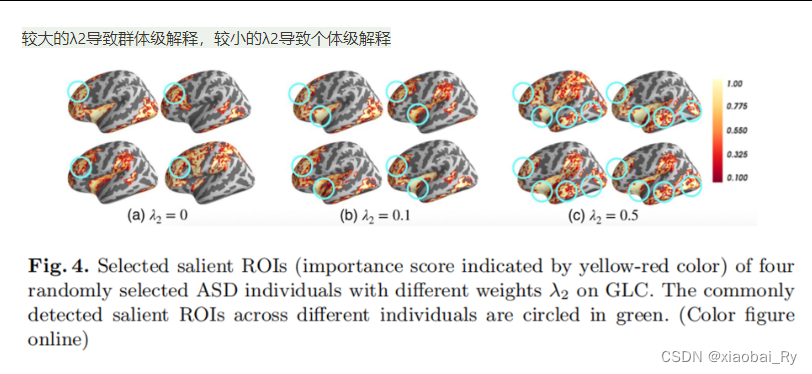
左高树

完整可编译运行代码见：Github::Data-Structures-Algorithms-and-Applications/_26maxHblt

定义

(大顶堆和小顶堆)堆结构是一种隐式数据结构(implicit data structure)。用完全二叉树表示的堆在数组中是隐式存储的(即没有明确的指针或其他数据能够用来重塑这种结构)。由于没有存储结构信息，这种表示方法的空间利用率很高，它实际上没有浪费空间。而且它的时间效率也很高。尽管如此，它并不适合于所有优先级队列的应用，尤其是当两个优先级队列或多个长度不同的队列需要合并的时候，这时我们就需要其他数据结构了。左高树就能满足这种需要。
考察一棵二叉树，它有一类特殊的节点叫做外部节点(external node)，它代替树中的空子树。其余节点叫做内部节点(internal node)。增加了外部节点的二叉树被称为扩充二叉树(extended binary tree)，图 12-6a 是一棵二叉树，其相应的扩充二叉树如图 12-6b 所示。外部节点用阴影框表示。为了方便起见，这些节点用 a~f标注。

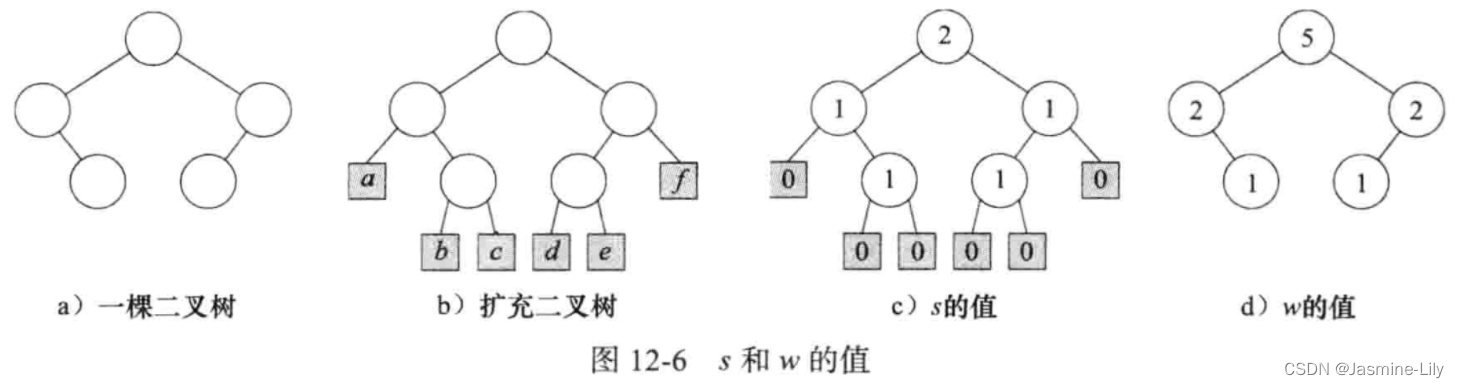
令s(x)是从节点x到其子树的外部节点的所有路径中最短的一条。根据s(x)的定义，若x是外部节点，则s的值为0；若x为内部节点，则s的值为
m i n { s ( L ) , s ( R ) } + 1 min\{s(L), s(R)\} + 1 min{s(L),s(R)}+1
其中L与R分别为x的左右孩子。扩充二叉树(如图12-6b所示)中各节点的s值如图12-6c所示。

定义 12-3 一棵二叉树称为高度优先左高树(height-biased leftist tree，HBLT)，当且仅当其任何一个内部节点的左孩子的s值都大于或等于右孩子的s值。

定理 12-1 令 x 为 HBLT 的一个内部节点，则

• 1)以x为根的子树的节点数目至少为$2^{S(x)}+1$。
• 2)若以x为根的子树有 m 个节点，那么 s(x)最多为$lo{g}_2(m+1)$。
• 3)从 x 到一外部节点的最右路径(即从 x 开始沿右孩子移动的路径)的长度为 s(x)。

证明 根据s(x)的定义，从x节点往下第s(x)-1层没有外部节点(否则x的s值将更小)。以x为根的子树在当前层只有1个节点x，下一层有2个节点，再下一层有4个节点……从x 层往下第 s(x)-1 层有$2^{s(x)-1}$个节点，在 s(x)-1 层以下可能还有其他节点，因此子树x 的节点数目至少为${\sum }_{i=0}^{s(x)-1}{2}^i=2^{s(x)}-1$。从1)可以推出 2)。根据s 的定义以及 HBLT 的一个节j=0点的左孩子的 s 值总是大于或等于其右孩子，可以推出 3)。

定义 12-4 若一棵HBLT 同时还是大根树，则称为最大 HBLT(maxHBLT)。若一棵HBLT 同时还是小根树，则称为最小 HBLT(min HBLT)。

如果我们考虑的不是路径长度，而是节点数目，那么我们可以得到另一种左高树。定义重量 w(x)是以节点x为根的子树的内部节点数目。若x是外部节点，则它的重量是0；若x是内部节点，则它的重量是其孩子节点的重量之和加1，在图12-6a的二叉树中，各节点的重量如图 12-6d 所示。

定义 12-5 一棵二叉树称为重量优先左高树(weight-biased leftist tree，WBLT)，当且仅当其任何一个内部节点的左孩子的w值都大于或等于右孩子的w值。若一棵WBLT同时还是大根树，则称为最大WBLT(max WBLT)。若一棵WBLT同时还是小根树，则称为最小WBLT(min WBLT)。

使用WBLT或HBLT，可以执行优先级队列的查找、插入(时间复杂度为logn)、删除操作(时间复杂度为logn)，其时间复杂性与堆相同。和堆一样，WBLT与HBLT可以在线性时间内完成初始化。用WBLT或HBLT表示的两个优先级队列可在对数时间内合并为一个(log(mn)，m表示x树的元素个数，n表示y树的元素个数)，而用堆表示的优先级队列做不到这一点。

插入删除合并算法

最大 HBLT 的插入

最大 HBLT 的插入操作可利用最大 HBLT 的合并操作来实现。假定将元素 × 插入名为 H的最大 HBLT 中。如果构建一棵仅有一个元素 x 的最大 HBLT，然后将它与 H 进行合并，那么合并后的最大HBLT将包括H的全部元素和元素x。因此，要插入一个元素，可以先建立一棵新的只包含这个元素的 HBLT，然后将这棵新的 HBLT 与原来的 HBLT 合并。

最大 HBLT 的删除

最大元素在根中。若根被删除，则分别以左右孩子为根的子树是两棵最大 HBLT。将这两棵最大HBLT合并，便是删除后的结果。因此，删除操作可以通过删除根元素之后的两棵子树的合并来实现。

两棵最大 HBLT 的合并

合并策略最好用递归来实现。令 A、B 为需要合并的两棵最大 HBLT。若一个为空，则另一个便是合并的结果。假设两者均不为空。为实现合并，先比较两个根元素，较大者作为合并后的根。假定A的根较大，且左子树为L。令C是A的右子树与B合并而成的HBLT。先将L作为合并树的左子树，C作为合并树的右子树，然后再比较L和C的weight，决定L和C是否交换。A与 B 合并的结果是以 A 为根，以L 和C为子树的最大 HBLT。如果 L 的s值小于 C 的 s值，则C为左子树，否则L为左子树。

meld仅沿着x和y的右子树移动，因此该函数的复杂性为O(s(x)+s(y))。因为s(x)和s(y)的最大值分别为$lo{g}_2(m+1)$和$lo{g}_2(n+1)$，其中m与n分别是x和y的元素个数，所以meld的时间复杂度为O(logm+logn)=O(log(mn))。

HBLT的初始化

初始化过程是将 n 个元素逐个插入最初为空的最大 HBLT。为得到具有线性时间的初始化算法，我们首先创建 n个仅含一个元素的最大HBLT，这 n 棵树组成一个 FIFO队列，然后从队列中依次成对删除 HBLT，然后将其合并后再插入队列末尾，直到队列只有一棵 HBLT 为止。时间复杂度为O(n)。

最大高度优先左高树的cpp实现

main.cpp

/*
Project name :			_26maxHblt
Last modified Date:		2023年12月14日10点20分
Last Version:			V1.0
Descriptions:			最大高度优先左高树——main函数
*/
#include "maxhblt.h"

int main() {
    maxhbltTest();
    return 0;
}

maxhblt.h

/*
Project name :			_26maxHblt
Last modified Date:		2023年12月14日10点20分
Last Version:			V1.0
Descriptions:			最大高度优先左高树——模板头文件
*/

#ifndef _26MAXHBLT_MAXHBLT_H
#define _26MAXHBLT_MAXHBLT_H

#include "maxPriorityQueue.h"
#include "maxHbltTreeNode.h"
#include "myExceptions.h"
#include <queue>
#include <sstream>

void maxhbltTest();

using namespace std;

template<class T>
class maxHblt : public maxPriorityQueue<T> {
public:
    maxHblt() {
        root = nullptr;
        treeSize = 0;
    }

    bool empty() const { return treeSize == 0; }

    int size() const { return treeSize; }

    const T &top() {// 返回最大元素
        if (treeSize == 0)
            throw queueEmpty();
        return root->element;
    }

    void pop();

    void push(const T &);

    void initialize(T *, int);

    void meld(maxHblt<T> &theHblt) {// 合并 *this 和 theHblt
        meld(root, theHblt.root);
        treeSize += theHblt.treeSize;
        theHblt.root = nullptr;
        theHblt.treeSize = 0;
    }

    void erase() {// 清空树
        postOrder(dispose);
        root = nullptr;
        treeSize = 0;
    }

    void postOrderOutput() {// 后序遍历输出树的元素
        postOrder(hbltOutput);
        cout << endl;
    }

    void postOrder(void(*theVisit)(maxHbltTreeNode<T> *)) {
        visit = theVisit;
        /*是因为递归，所以才要这样的*/
        postOrder(root);/*这里调用的是静态成员函数inOrder()*/
    }

private:
    maxHbltTreeNode<T> *root;//指向根的指针
    int treeSize;//树的结点个数
    void meld(maxHbltTreeNode<T> *&,
              maxHbltTreeNode<T> *&);// 合并两颗树

    static void (*visit)(maxHbltTreeNode<T> *);//是一个函数指针,返回值为void 函数参数为maxHbltTreeNode<T>*
    static void dispose(maxHbltTreeNode<T> *t) { delete t; }

    static void postOrder(maxHbltTreeNode<T> *t);

    static void hbltOutput(maxHbltTreeNode<T> *t) { cout << t->element << ' '; }
};

template<class T>
void (*maxHblt<T>::visit)(maxHbltTreeNode<T> *) = 0;      // visit function

template<class T>
void maxHblt<T>::meld(maxHbltTreeNode<T> *&x,
                      maxHbltTreeNode<T> *&y) {// 合并两棵最大高度优先左高树
    // x是合并后的树
    if (y == nullptr)   // y是空树，直接返回
        return;
    if (x == nullptr)   // x是空树，将y赋值给x，返回
    {
        x = y;
        return;
    }
    // x树永远是提供根的树
    // x和y都不是空树，如果x的元素小于y的元素，则交换x树和y树
    if (x->element < y->element)
        swap(x, y);

    // 现在 x->element.second >= y->element.second
    // 合并x的右子树和y树,x的根和左子树作为合并树的根和左子树
    meld(x->rightChild, y);// 得到的x的右子树就是x的右子树与y树合并的最大高度优先左高树

    // 如果需要，交换x的左子树和右子树的值
    if (x->leftChild == nullptr) {// 如果x的左子树为空, 则将x的左子树和右子树做交换，保证x的左子树比右子树高
        x->leftChild = x->rightChild;
        x->rightChild = nullptr;
        x->height = 1;
    } else {// 如果x的左子树的weight小于右子树的weight，则要交换左右子树的值
        if (x->leftChild->height < x->rightChild->height)
            swap(x->leftChild, x->rightChild);
        x->height = x->rightChild->height + 1;// 存储小的那一个
    }
}

template<class T>
void maxHblt<T>::push(const T &theElement) {// 向树中插入元素
    // 创建一个新的节点
    maxHbltTreeNode<T> *q = new maxHbltTreeNode<T>(theElement, 1);

    // 将新节点与root树合并
    meld(root, q);
    treeSize++;
}

template<class T>
void maxHblt<T>::pop() {// 删除最大元素
    if (root == nullptr)
        throw queueEmpty();

    // 当树不为空时
    maxHbltTreeNode<T> *left = root->leftChild,
            *right = root->rightChild;
    delete root;
    root = left;
    meld(root, right);
    treeSize--;
}

template<class T>
void maxHblt<T>::initialize(T *theElements, int theSize) {// 初始化hblt 使用theElements[1:theSize].
    queue<maxHbltTreeNode<T> *> q;
    erase();  // 清空左高树

    for (int i = 1; i <= theSize; i++)
        // 创建节点，全部放入队列中
        q.push(new maxHbltTreeNode<T>(theElements[i]));

    // 不断取出两个节点进行合并
    for (int i = 1; i <= theSize - 1; i++) {
        maxHbltTreeNode<T> *b = q.front();
        q.pop();
        maxHbltTreeNode<T> *c = q.front();
        q.pop();
        meld(b, c);
        // 合并生成的树放到队列中
        q.push(b);
    }

    if (theSize > 0)
        root = q.front();
    treeSize = theSize;
}

/*后序遍历 递归*/
template<class T>
void maxHblt<T>::postOrder(maxHbltTreeNode<T> *t) {
    if (t != nullptr) {
        postOrder(t->leftChild);/*后序遍历左子树*/
        postOrder(t->rightChild);/*后序遍历右子树*/
        visit(t);/*访问树根*/
    }
}

#endif //_26MAXHBLT_MAXHBLT_H

maxhblt.cpp

/*
Project name :			_26maxHblt
Last modified Date:		2023年12月14日10点20分
Last Version:			V1.0
Descriptions:			最大高度优先左高树——测试函数
*/

#include <iostream>
#include "maxhblt.h"

using namespace std;

void maxhbltTest()
{
    maxHblt<int> h, j;
    int a[6] = {0, 7, 9, 1, 8, 11};
    h.initialize(a, 5);
    cout << "One tree in postorder is" << endl;
    cout << "Tree size is " << h.size() << endl;
    h.postOrderOutput();
    int b[5] = {0, 2, 6, 4, 9};

    j.initialize(b,4);
    cout << "Other tree in postorder is" << endl;
    cout << "Tree size is " << j.size() << endl;
    j.postOrderOutput();

    h.meld(j);
    cout << "After melding, the tree in postorder is" << endl;
    cout << "Tree size is " << h.size() << endl;
    h.postOrderOutput();

    int w = h.top();
    h.pop();
    int x = h.top();
    h.pop();
    int y = h.top();
    h.pop();
    int z = h.top();
    h.pop();
    cout << "After popping four elements, the tree is" << endl;
    cout << "Tree size is " << h.size() << endl;
    h.postOrderOutput();
    cout << "The popped elements, in order, are" << endl;
    cout << w << "  " << x << "  " << y << "  " << z << endl;

    h.push(10);
    h.push(20);
    h.push(5);
    cout << "After pushing 10, 20 & 5, the tree is" << endl;
    cout << "Leftist tree in postorder" << endl;
    cout << "Tree size is " << h.size() << endl;
    h.postOrderOutput();

    h.push(15);
    h.push(30);
    h.push(2);
    cout << "After pushing 15, 30 & 15, the tree is" << endl;
    cout << "Leftist tree in postorder" << endl;
    cout << "Tree size is " << h.size() << endl;
    h.postOrderOutput();

    cout << "The max element is " << h.top() << endl;

    cout << "Popped max element " << h.top() << endl;
    h.pop();
    cout << "Leftist tree in postorder" << endl;
    cout << "Tree size is " << h.size() << endl;
    h.postOrderOutput();

    x = h.top();
    h.pop();
    cout << "Popped max element " << x << endl;
    cout << "Tree size is " << h.size() << endl;
    cout << "Leftist tree in postorder" << endl;
    h.postOrderOutput();

    while (true)
    {
        try
        {
            x = h.top();
            h.pop();
            cout << "Popped max element " << x << endl;
            cout << "Tree size is " << h.size() << endl;
        }
        catch(queueEmpty) {break;}
    }
}

maxPriorityQueue.h

/*
Project name :			_26maxHblt
Last modified Date:		2023年12月14日10点20分
Last Version:			V1.0
Descriptions:			优先级队列——虚基类
*/

#ifndef _26MAXHBLT_MAXPRIORITYQUEUE_H
#define _26MAXHBLT_MAXPRIORITYQUEUE_H
using namespace std;

template<class T>
class maxPriorityQueue
{
public:
    virtual ~maxPriorityQueue() {}
    virtual bool empty() const = 0;
    // return true iff queue is empty
    virtual int size() const = 0;
    // return number of elements in queue
    virtual const T& top() = 0;
    // return reference to the max element
    virtual void pop() = 0;
    // remove the top element
    virtual void push(const T& theElement) = 0;
    // add theElement to the queue
};
#endif //_26MAXHBLT_MAXPRIORITYQUEUE_H

maxHbltTreeNode.h

/*
Project name :			_26maxHblt
Last modified Date:		2023年12月14日10点20分
Last Version:			V1.0
Descriptions:			最大高度优先左高树——树的节点类
*/

#ifndef _26MAXHBLT_MAXHBLTTREENODE_H
#define _26MAXHBLT_MAXHBLTTREENODE_H
template<class T>
struct maxHbltTreeNode
{
    int height;// 存储权重
    T element;
    maxHbltTreeNode<T>* leftChild,//左子树
    *rightChild;//右子树
    /*默认构造函数*/
    maxHbltTreeNode() { leftChild = rightChild = nullptr; height = 0; element = 0;}
    /*只初始化element*/
    explicit maxHbltTreeNode(T melement)
    {
        element = melement;
        height = 1;
        leftChild = rightChild = nullptr;
    }
    maxHbltTreeNode(T melement, int mheight)
    {
        element = melement;
        height = mheight;
        leftChild = rightChild = nullptr;
    }
    /*三个元素都初始化*/
    maxHbltTreeNode(T& melement, int mheight, maxHbltTreeNode<T>* mleftChild, maxHbltTreeNode<T>* mrightChild)
    {
        element = melement;
        height = mheight;
        leftChild = mleftChild;
        rightChild = mrightChild;
    }
};
#endif //_26MAXHBLT_MAXHBLTTREENODE_H

myExceptions.h

/*
Project name :			allAlgorithmsTest
Last modified Date:		2022年8月13日17点38分
Last Version:			V1.0
Descriptions:			综合各种异常
*/
#pragma once
#ifndef _MYEXCEPTIONS_H_
#define _MYEXCEPTIONS_H_
#include <string>
#include<iostream>
#include <utility>

using namespace std;

// illegal parameter value
class illegalParameterValue : public std::exception
{
public:
    explicit illegalParameterValue(string theMessage = "Illegal parameter value")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// illegal input data
class illegalInputData : public std::exception
{
public:
    explicit illegalInputData(string theMessage = "Illegal data input")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// illegal index
class illegalIndex : public std::exception
{
public:
    explicit illegalIndex(string theMessage = "Illegal index")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// matrix index out of bounds
class matrixIndexOutOfBounds : public std::exception
{
public:
    explicit matrixIndexOutOfBounds
            (string theMessage = "Matrix index out of bounds")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// matrix size mismatch
class matrixSizeMismatch : public std::exception
{
public:
    explicit matrixSizeMismatch(string theMessage =
    "The size of the two matrics doesn't match")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// stack is empty
class stackEmpty : public std::exception
{
public:
    explicit stackEmpty(string theMessage =
    "Invalid operation on empty stack")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// queue is empty
class queueEmpty : public std::exception
{
public:
    explicit queueEmpty(string theMessage =
    "Invalid operation on empty queue")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// hash table is full
class hashTableFull : public std::exception
{
public:
    explicit hashTableFull(string theMessage =
    "The hash table is full")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// edge weight undefined
class undefinedEdgeWeight : public std::exception
{
public:
    explicit undefinedEdgeWeight(string theMessage =
    "No edge weights defined")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};

// method undefined
class undefinedMethod : public std::exception
{
public:
    explicit undefinedMethod(string theMessage =
    "This method is undefined")
    {message = std::move(theMessage);}
    void outputMessage() {cout << message << endl;}
private:
    string message;
};
#endif

运行结果

"C:\Users\15495\Documents\Jasmine\prj\_Algorithm\Data Structures, Algorithms and Applications in C++\_26maxHblt\cmake-build-debug\_26maxHblt.exe"
One tree in postorder is
Tree size is 5
7 9 1 8 11
Other tree in postorder is
Tree size is 4
4 2 6 9
After melding, the tree in postorder is
Tree size is 9
1 2 6 8 4 9 7 9 11
After popping four elements, the tree is
Tree size is 5
2 4 6 1 7
The popped elements, in order, are
11  9  9  8
After pushing 10, 20 & 5, the tree is
Leftist tree in postorder
Tree size is 8
2 4 6 1 7 10 5 20
After pushing 15, 30 & 15, the tree is
Leftist tree in postorder
Tree size is 11
2 4 6 1 7 10 5 15 20 2 30
The max element is 30
Popped max element 30
Leftist tree in postorder
Tree size is 10
5 2 15 2 4 6 1 7 10 20
Popped max element 20
Tree size is 9
Leftist tree in postorder
2 4 6 1 7 2 10 5 15
Popped max element 15
Tree size is 8
Popped max element 10
Tree size is 7
Popped max element 7
Tree size is 6
Popped max element 6
Tree size is 5
Popped max element 5
Tree size is 4
Popped max element 4
Tree size is 3
Popped max element 2
Tree size is 2
Popped max element 2
Tree size is 1
Popped max element 1
Tree size is 0

Process finished with exit code 0