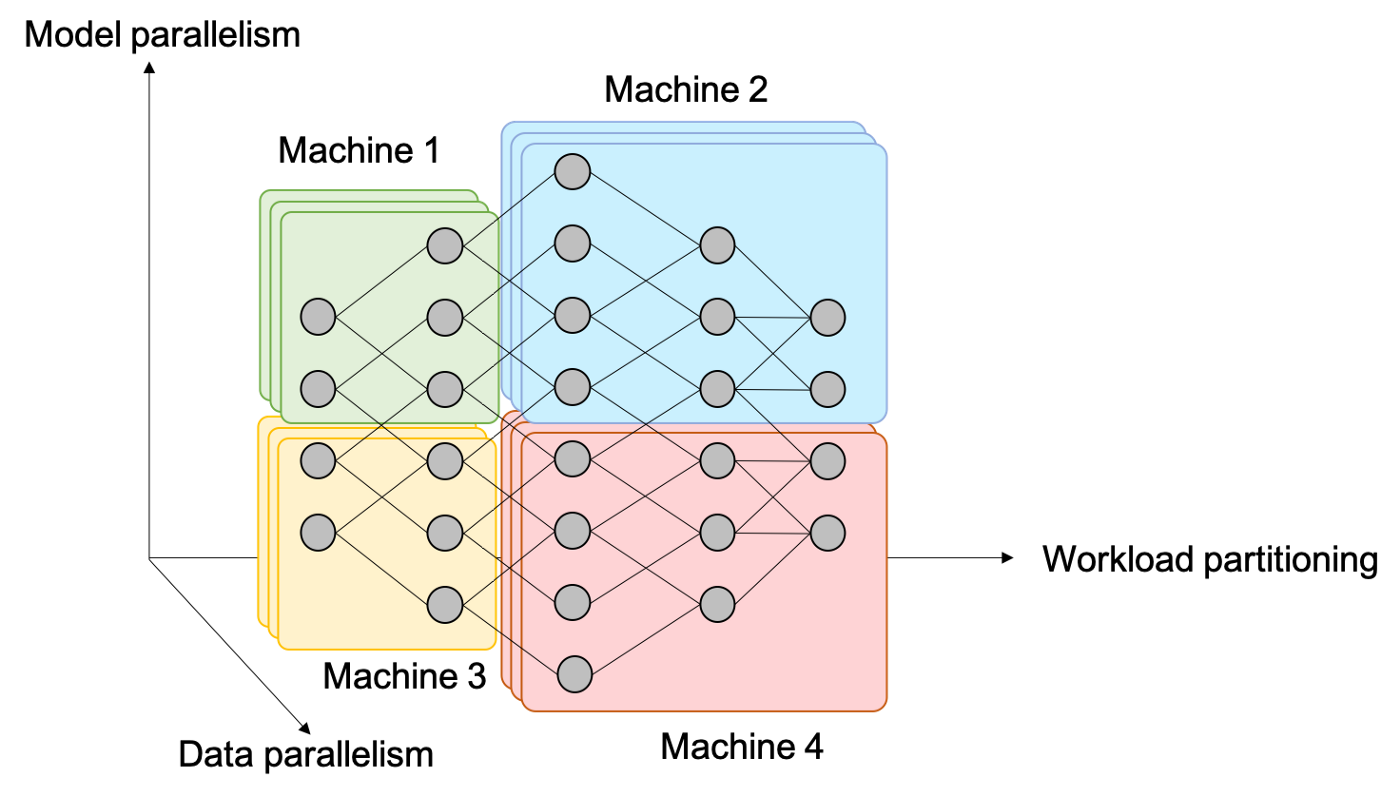
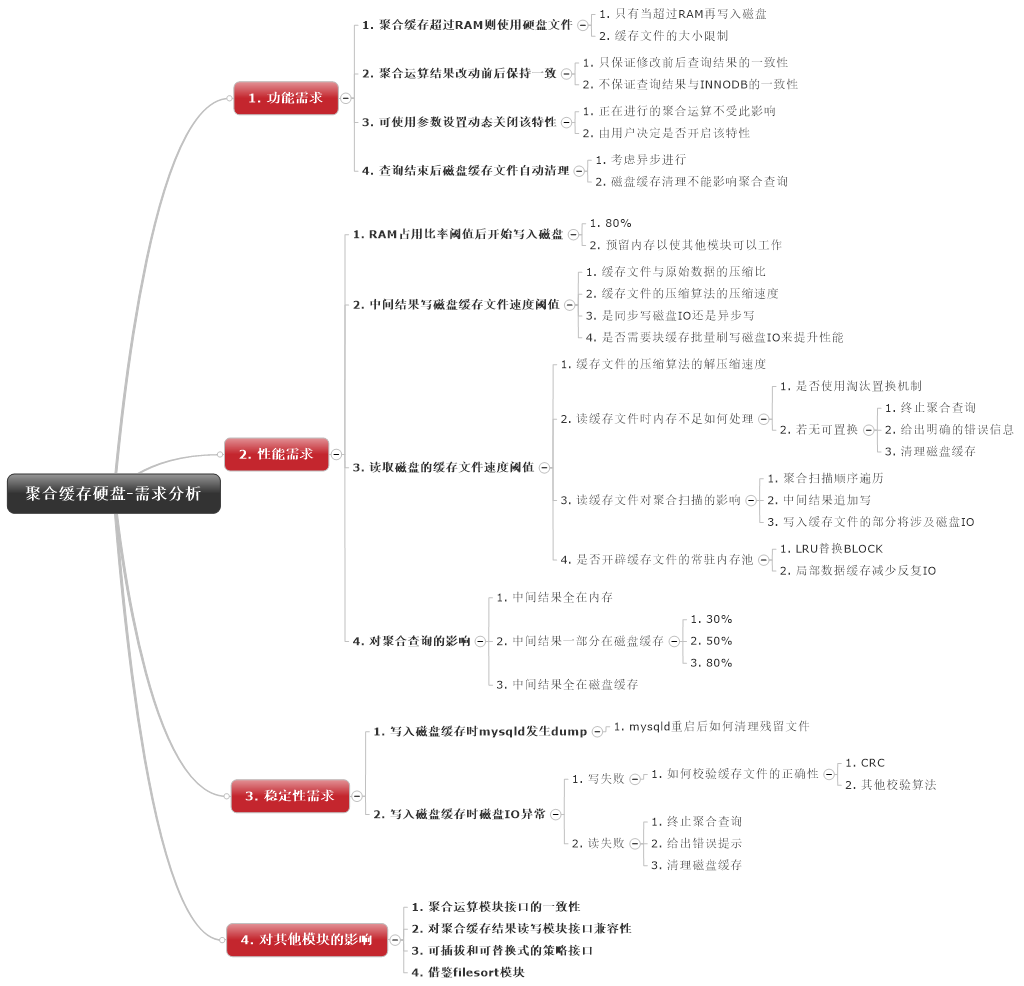
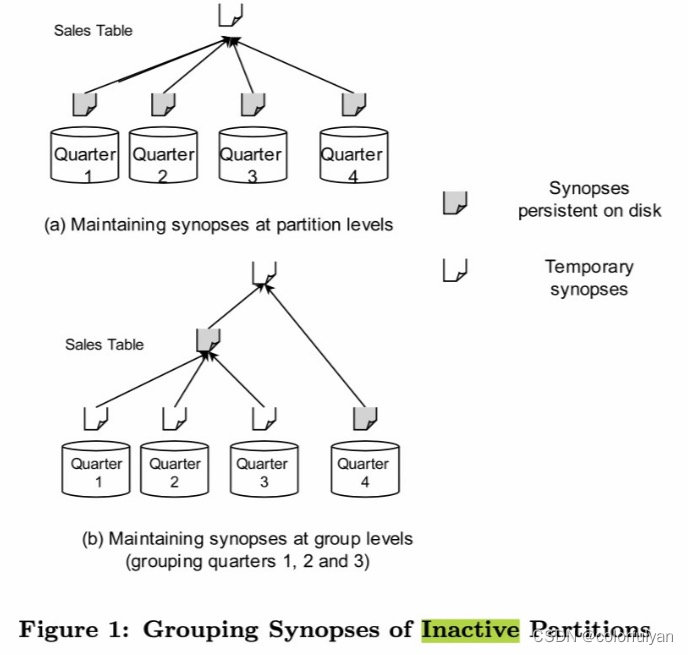
我国网络技术水平的提升，带动着WEB前端业务量的显著增长，人们对于网络服务的需求也日益复杂，与此同时，越来越多的黑客出现，其攻击水平也有了明显提升，WEB前端也成为了众多黑客进行网络攻击的主要目标。

因此，开发者在进行网站建设，运营者在进行网站维护的过程中，不但要确保服务器的安全性，也应加强对WEB前端安全性的保护。

Gartner对安全架构的定义是：安全架构是计划和设计组织的、概念的、逻辑的、物理的组件的规程和相关过程，这些组件以一致的方式进行交互，并与业务需求相适应，以达到和维护一种安全相关风险可被管理的状态。

因此，安全架构的概念非常宽泛，包括安全控制措施、安全服务（例如身份验证、访问控制等）和安全产品（例如防火墙、入侵检测等）。

前端安全问题

近年来有8大问题尤其引起关注：

• 跨站脚本攻击（Cross-SiteScripting）
• 使用iframe的风险
• 点击劫持
• 错误的内容推断
• 不安全的第三方依赖包
• HTTPS中间人攻击
• 本地存储数据泄露
• CDN劫持/污染

如此多的、影响重大的前端安全问题，直接把软件安全防范推上了风口浪尖，安全人员面临着挑战也倍数级增长。

Web前端安全问题产生原因

现实原因

随着网络的普及和Web应用的丰富，在互联网上人们可以开展各类活动，如购物、游戏、网上银行、社交平台等，这些服务网站上有大量用户资金相关的隐私信息如银行账户、密码、个人身份信息、电话号码等。

这些信息可以直接或间接被不法分子窃取和利用，从而对最终用户造成损失。

巨大的利益诱惑是产生Web安全问题的动机。

技术原因

在技术层面，Web服务是建立在HTTP协议上的，HTTP又是建立在TCP/IP之上，在TCP/IP设计之初是没有考虑安全问题的，所有的安全问题需要Web服务提供者自己考虑，这使得在网络上传输的数据是没有任何安全保护。

攻击者可以利用系统漏洞造成进程缓冲区溢出，或者利用系统漏洞来进行用户提权运行任意程序，甚至安装和运行恶意木马程序，窃取用户机密数据。在Web应用开发时由于大部分开发者把精力放到业务逻辑实现而非Web安全性上，导致Web程序本身存在很多漏洞，如缓冲区溢出、SQL注入等。

开发人员的乐观

大部分的开发人员是乐观的，认为自己开发的Web网站很安全，如网站已经通过成熟的Web开发框架或采用了一些安全传输技术如SSL或做了完善的数据备份，所以没有什么安全风险，产生这种原因的根源是大部分开发人员对Web安全问题认识不足或不全，片面乐观导致。

端侧安全的主流解决方案

1、 APP 运行时保护

对移动端应用的逆向分析还有动态调试。通过动态调试还可以伪造或篡改请求 / 响应包，从而攻击服务器端。

此种攻击可以采用市场上的一些加固工具软件对APP 进行加固保护，防止恶意破解、反编译、二次打包等。

2、APP 代码保护

由于开源技术的进步，攻击者很容易就可以获得应用的反编译代码（基本是应用源代码）。

针对此攻击，提高逆向分析的门槛，可以进行代码混淆、dex 加壳、so 加壳等方式对代码进行保护。

3、App第三方代码安全

移动应用开发过程中，出于功能需求等原因，开发人员不可避免会集成一些其他第三方提供的代码，如 SDK。

这些第三方代码未经测试和评估就直接嵌入到应用中直接使用，容易出现不可预料的后果。

一方面是第三方代码的安全性未经测试，可能存在安全漏洞被攻击者利用，从而威胁整个应用的正常使用。
另一方面，第三方代码额外实现了冗余功能或者申请多余的特权，可能造成用户隐私信息泄露，或者一系列恶意行为。

对于此类威胁，安全设计方案是：

1）App中大部分是web或者小程序类轻应用，可以采用市面上的安全沙箱类技术（如：FinClip），对应用进行统一的上下架管理。其特点主要体现在三个方面：

沙箱内小程序之间的隔离
沙箱对运行其中的小程序代码，隔离其对宿主环境的资源访问。
沙箱隔离了宿主对于沙箱中运行的小程序所产生的数据。

2）集成第三方代码时，开发人员应尽可能了解第三方代码的功能，以及尽可能保证第三方代码的安全性。

4、APP 端业务安全

为了防止 APP 用户恶意注册及薅羊毛等恶意行为，可以在 APP 中加入设备指纹，进行数据埋点等，将 APP 数据接入业务风控平台，进行业务反欺诈。

5、Web 安全

对于 Web 安全，关注常见的 OWASP TOP 10 漏洞，如注入、身份认证、敏感信息泄露、安全配置错误等。常见的防御措施有认证、授权、加密、审计、输入验证等。

6、Restful API 安全

Restful API 以 URI 方式对外提供数据服务或功能服务。外部用户多数情况下是程序或系统。

提供的数据服务或功能服务多数情况下，是非公开的，即需要对 HTTP 请求来源和身份做识别与认证，再经过授权决策（访问控制）后，提供相应的数据或执行功能。

结语

介绍了Web前端安全问题产生原因，然后给出了对应的解决策略，从而降低和避免网站被攻击的可能性，另外可以看到Web安全是一个很大的课题，Web前端安全仅是其中的一个最前端和常见的领域，也可以看到要开发一个安全性非常高的Web安全网站是多么困难，

但随着技术的发展，特别是量子计算机通信的出现，未来必然会出现超越现在已知的安全技术。