作者:@小萌新
专栏:@数据结构进阶
作者简介:大二学生 希望能和大家一起进步!
本篇博客简介:介绍几道二叉树的oj题
题目一 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示
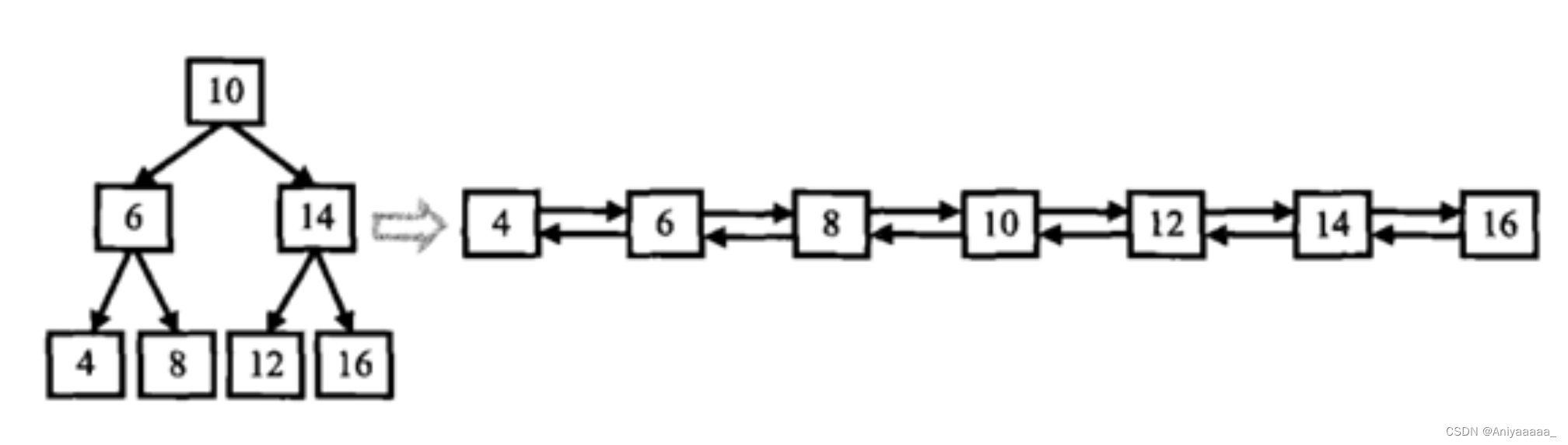
数据范围:输入二叉树的节点数 0 \le n \le 10000≤n≤1000,二叉树中每个节点的值 0\le val \le 10000≤val≤1000
要求:空间复杂度O(1)O(1)(即在原树上操作),时间复杂度 O(n)O(n)
看到搜索二叉树的排序就应该能想到要中序遍历
因此我们首先要写一个中序遍历的子函数
void Inorder(TreeNode*cur ,TreeNode*& prev)
{
if (cur == nullptr)
{
return;
}
Inorder(cur->left, prev);
Inorder(cur->right, prev);
}
然后因为题目中要求的连接操作
我们将左指针当作前驱指针 右指针都当作后继指针 就能写出下面的代码
void Inorder(TreeNode*cur ,TreeNode*& prev)
{
if (cur == nullptr)
{
return;
}
Inorder(cur->left, prev);
cur->left = prev;
if (prev)
{
prev->right = cur;
}
prev = cur;
Inorder(cur->right, prev);
}
再之后我们就需要找到最小的一个节点 也就是最左边的节点
由于上面我们已经将整个二叉树变成了一个循环双向链表了
所以说我们这个时候设置一个指针 不停的往前找就能找到
当然这个时候也不能忽略本来二叉树就为空的情况
代码和运行结果如下
class Solution {
public:
void Inorder(TreeNode*cur ,TreeNode*& prev)
{
if (cur == nullptr)
{
return;
}
Inorder(cur->left, prev);
cur->left = prev;
if (prev)
{
prev->right = cur;
}
prev = cur;
Inorder(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr)
{
return nullptr;
}
TreeNode* prev = nullptr;
Inorder(pRootOfTree, prev);
TreeNode* cur = pRootOfTree;
while (cur->left) {
cur = cur->left;
}
return cur;
}
};
题目二 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal
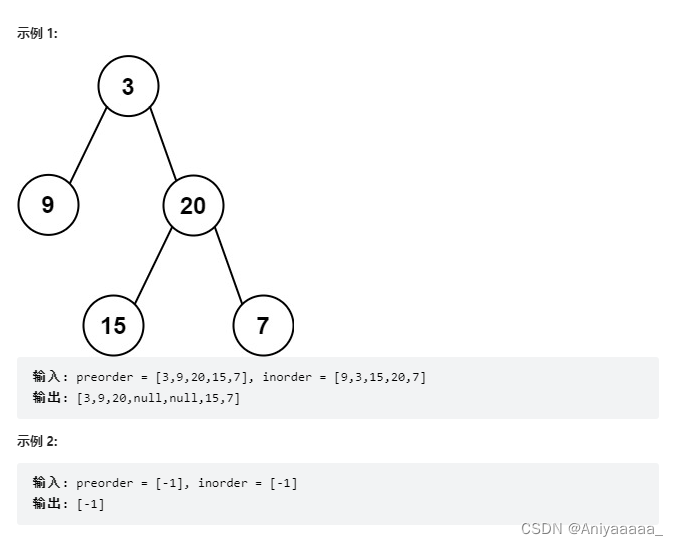
首先 不管是前序遍历还是后续遍历我们都能够否很轻松的确定根所在的位置
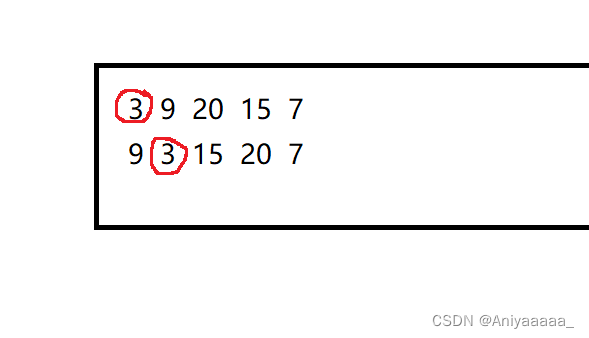
之后我们通过根的位置还有中序遍历的特性遍能将二叉树分成三个部分

分成这三部分之后我们就可以很简单的使用递归来完成这颗二叉树了
if (inbegin > inend)
{
return nullptr;
}
TreeNode* root = new TreeNode(preorder[prei]);
int rooti = inbegin;
while (rooti <= inend)
{
if (inorder[rooti] == preorder[prei])
{
break;
}
else
{
rooti++;
}
}
如果说左右区间 有一个为空 那么我们就不管了 返回一个空指针
如果不为空 我们找到根节点在哪里 之后递归左右节点
root->left = _buildtree(preorder, inorder, prei , inbegin , rooti -1 );
root->right = _buildtree(preorder, inorder, prei , rooti + 1 , inend);
return root;
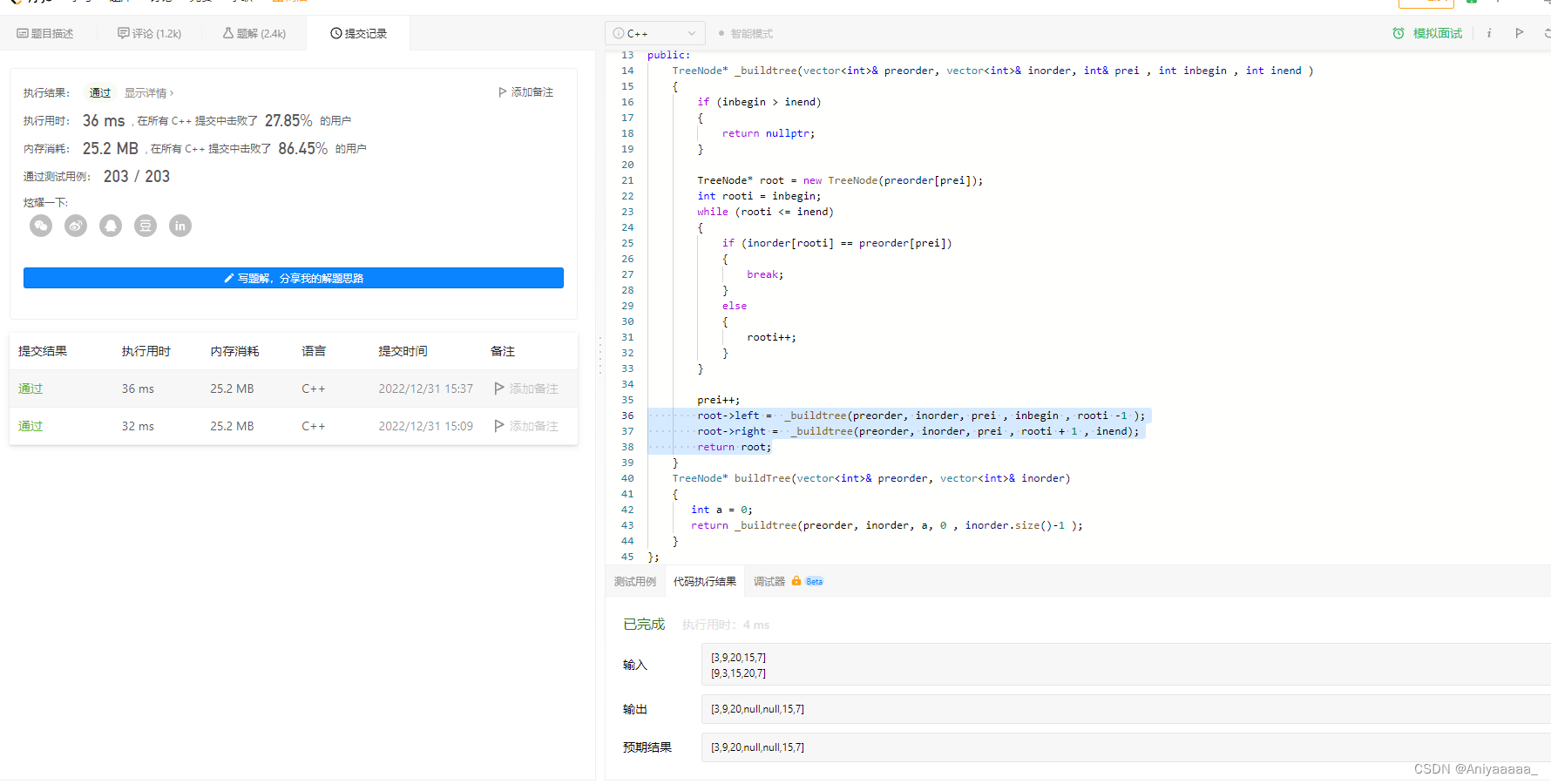
完整代码和运行结果如下
class Solution {
public:
TreeNode* _buildtree(vector<int>& preorder, vector<int>& inorder, int& prei , int inbegin , int inend )
{
if (inbegin > inend)
{
return nullptr;
}
TreeNode* root = new TreeNode(preorder[prei]);
int rooti = inbegin;
while (rooti <= inend)
{
if (inorder[rooti] == preorder[prei])
{
break;
}
else
{
rooti++;
}
}
prei++;
root->left = _buildtree(preorder, inorder, prei , inbegin , rooti -1 );
root->right = _buildtree(preorder, inorder, prei , rooti + 1 , inend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
int a = 0;
return _buildtree(preorder, inorder, a, 0 , inorder.size()-1 );
}
};
题目三 二叉树的非递归中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
一道很简单的题目 能A过这道题的代码应该是这么写的
class Solution {
public:
vector<int> ans;
vector<int> inorderTraversal(TreeNode* root)
{
if (root == nullptr)
{
return ans;
}
inorderTraversal(root -> left);
ans.push_back(root -> val);
inorderTraversal(root -> right);
return ans;
}
};
然后我们再这里再添加一个限制条件 不能使用递归
我们都知道 因为栈这种数据结构的存在
所有的递归都可以改写成非递归形式
对于二叉树这种数据结构来说也是一样子的
我们首先将二叉树的左子树全部入栈
之后开始取出左子树的节点记录 并且入栈右子树
代码表示如下
class Solution {
public:
vector<int> ans;
stack<TreeNode*> st1;
vector<int> inorderTraversal(TreeNode* root)
{
TreeNode* cur = root;
while (cur || !st1.empty())
{
while (cur)
{
st1.push(cur);
cur = cur -> left;
}
TreeNode* top = st1.top();
st1.pop();
ans.push_back(top -> val);
// 右子树
cur = top -> right;
}
return ans;
}
};