0 结果

请添加图片描述

1 题目

在这里插入图片描述

2 思路

1，首先明确二叉搜索树的定义：任何一个节点大于其左子树中的全部结点，小于其右子树中的全部结点。中序遍历二叉搜索树得到一个升序序列。
2，明确题目中给出的顺序存储的二叉搜索树的结点特点：根结点存储在SqBiTNode[0]；当某个结点存储在SqBiTNode[i]中时，若有左孩子，则其值保存在SqBiTNode[2i+1]中，若有右孩子，保存在SqBiTNode[2i+2]中，若有双亲结点保存在SqBiTNode[(i-1)/2]中；
3，
- 3.1 思路一：（利用中序遍历搜查搜索数得到的是一个升序序列的性质）使用整型变量val（初值为负数）记录中序遍历过程中已遍历结点的最大值，若当前遍历的结点值小于等于val，则返回false；否则，将val的值更新为当前结点的值。
- 3.2 思路二：（利用二叉搜索树的定义）从最后一个叶结点向前遍历树，判断是否满足结点与子树之间的大小关系（结点大于左子树，小于右子树），使用pmax和pmin数组分别存储右子树中结点最大值（子树中最大值）、左子树结点的最小值（子树中最小值）（比较结点值时，若是左孩子结点，使用该节点值的双亲结点值比较该结点的右子树最大值；若是右孩子结点，使用该节点值的双亲结点值比较该节点的左子树的最小值）。

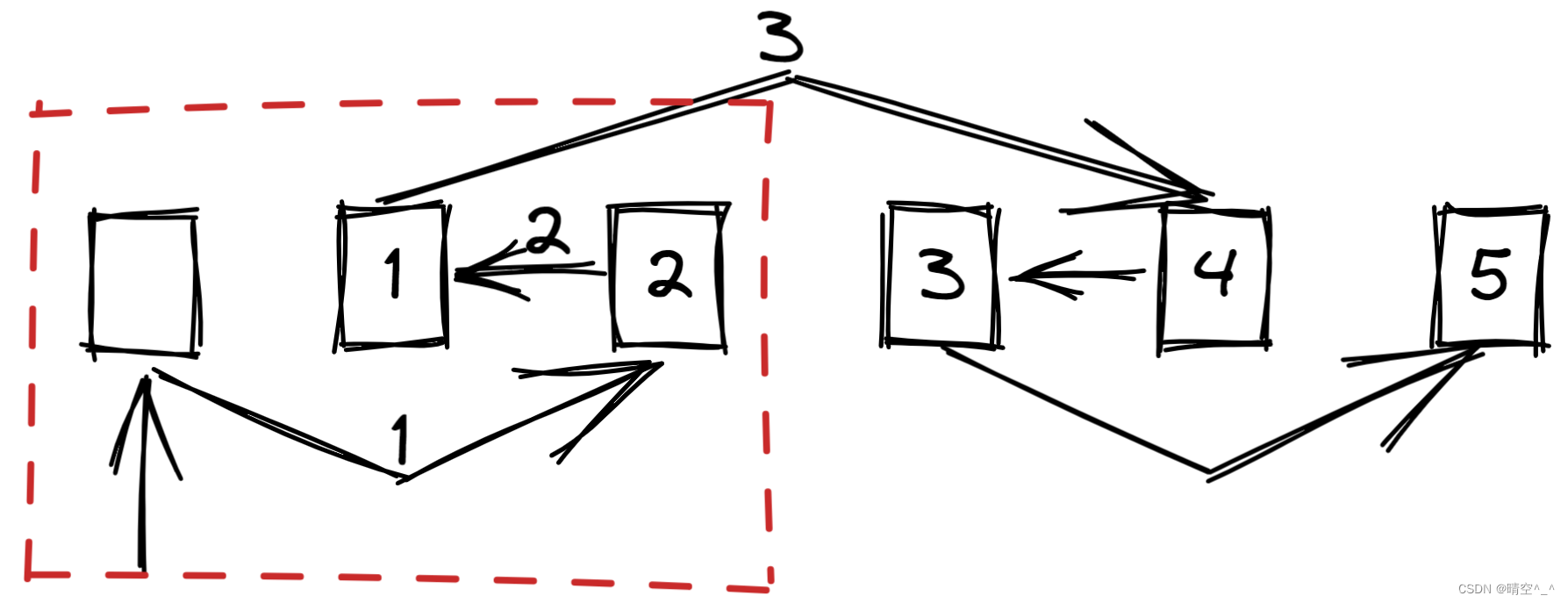
注意⚠️：如果直接判断左<中<右，就会出现错误，例如下面的例子。
在这里插入图片描述

3 实现

3.1 思路1

运行二叉树T2的过程说明：

1，首先执行语句1（前提：k：0，val：-1）；
2，执行语句2（结果：k：1，val：-1）【栈：2】；
3，执行语句1（前提：k：1， val：-1，bt.SqBiTNode[k]：-1）；
4，执行语句2（结果：k：3， val：-1，bt.SqBiTNode[k]：-1）【栈：2， 2】；
5，执行语句1（前提：k：3，val：-1）
6，执行语句6（前提：k：3，val：-1）；
7，执行语句3（前提：k：1，val：-1）【栈：2】；
8，执行语句4（前提：k：1，val：-1，bt.SqBiTNode[k]：50）；
9，执行语句5（结果：k：4，val：50）【栈：2，5】；
10，执行语句1（前提：k：4，val：50）；
11，执行语句2（结果：k：9，val：50）【栈：2，5，2】；
12 ，执行语句1（前提：k：9，val：50）；
13，执行语句6（前提：k：9，val：50）；
14，执行语句2（前提：k：4，val：50）【栈：2，5】；
15，执行语句3（前提：k：4，val：50，bt.SqBiTNode[k]：30，不满足条件）；
16，执行语句7（前提：k：4，val：50）；
17，执行语句5（前提：k：1，val：50）【栈：2】；
18，执行语句7（前提：k：1，val：50）；
19，执行语句2（前提：k：0，val：50）【栈：】；
20，执行语句7（前提：k：0，val：50，返回false）；

#include<iostream>
#include <vector>
const int MAX_SIZE = 11;//T1：10;T2:11

typedef struct {
    int SqBiTNode[MAX_SIZE];
    int ElemNum;
}SqBiTree;


bool judgeInOrderBST(SqBiTree bt, int k, int *val){//初始时，k为0;使用val的地址，是为了在每次递归时更新val值
    if(k < bt.ElemNum && bt.SqBiTNode[k] != -1){//遍历树中每个非空结点【语句1】
        if(!judgeInOrderBST(bt, 2*k + 1, val)) return false;//如果有一个结点不满足升序条件，则返回false【语句2】
        if(bt.SqBiTNode[k] <= *val) return false;//与之前保存的元素比较【语句3】
        *val = bt.SqBiTNode[k];//中序遍历，更新val的值为当前结点的值【语句4】
        if(!judgeInOrderBST(bt, 2*k + 2, val)) return false;//【语句5】
    }
    return true;【//语句6】
	//【语句7】
}

int main(){

    SqBiTree bt;

    //创建二叉树T1
//    bt.ElemNum = 10;
//    bt.SqBiTNode[0] = 40;
//    bt.SqBiTNode[1] = 25;
//    bt.SqBiTNode[2] = 60;
//    bt.SqBiTNode[3] = -1;
//    bt.SqBiTNode[4] = 30;
//    bt.SqBiTNode[5] = -1;
//    bt.SqBiTNode[6] = 80;
//    bt.SqBiTNode[7] = -1;
//    bt.SqBiTNode[8] = -1;
//    bt.SqBiTNode[9] = 27;

    //创建二叉树T2
    bt.ElemNum = 11;
    bt.SqBiTNode[0] = 40;
    bt.SqBiTNode[1] = 50;
    bt.SqBiTNode[2] = 60;
    bt.SqBiTNode[3] = -1;
    bt.SqBiTNode[4] = 30;
    bt.SqBiTNode[5] = -1;
    bt.SqBiTNode[6] = -1;
    bt.SqBiTNode[7] = -1;
    bt.SqBiTNode[8] = -1;
    bt.SqBiTNode[9] = -1;
    bt.SqBiTNode[10] = 35;

    int val = -1;
    std::string res = judgeInOrderBST(bt, 0, &val)?"是":"否";
    std::cout<<"判断是否是二叉搜索树："<<res;
    return 0;
}

3.2 思路二

#include<iostream>
#include <vector>
const int MAX_SIZE = 11;//T1：10;T2:11

typedef struct {
    int SqBiTNode[MAX_SIZE];
    int ElemNum;
}SqBiTree;


bool judgeInOrderBST(SqBiTree bt, int k, int *val){//初始时，k为0;使用val的地址，是为了在每次递归时更新val值
    if(k < bt.ElemNum && bt.SqBiTNode[k] != -1){//遍历树中每个非空结点
        if(!judgeInOrderBST(bt, 2*k + 1, val)) return false;//如果有一个结点不满足升序条件，则返回false
        if(bt.SqBiTNode[k] <= *val) return false;//与之前保存的元素比较
        *val = bt.SqBiTNode[k];//更新val的值为当前结点的值
        if(!judgeInOrderBST(bt, 2*k + 2, val)) return false;
    }
    return true;
}

bool judgeBST(SqBiTree bt){
    int k, m, *pmax, *pmin;
    pmin = new int[bt.ElemNum];//或者pmin = (int*) malloc(sizeof (int) * bt.ElemNum);
    pmax = new int[bt.ElemNum];
    for (k = 0; k < bt.ElemNum; k++) {//初始化辅助数组
        pmin[k] = pmax[k] = bt.SqBiTNode[k];
    }
    for(k = bt.ElemNum -1; k > 0;k--){//从最后一个结点向根结点遍历
        if(bt.SqBiTNode[k] != -1){
            m=(k-1)/2;//双亲结点
            if(k % 2 == 1 && bt.SqBiTNode[m] > pmax[k]){//左孩子；双亲结点值大于右孩子最大值
                pmin[m] = pmin[k];
            }else if(k % 2 == 0 && bt.SqBiTNode[m] < pmin[k]){//右孩子；双亲结点值小于左孩子最大值
                pmax[m] = pmax[k];
            }else{
                return false;
            }
        }
    }
    return true;
}

int main(){

    SqBiTree bt;

    //创建二叉树T1
//    bt.ElemNum = 10;
//    bt.SqBiTNode[0] = 40;
//    bt.SqBiTNode[1] = 25;
//    bt.SqBiTNode[2] = 60;
//    bt.SqBiTNode[3] = -1;
//    bt.SqBiTNode[4] = 30;
//    bt.SqBiTNode[5] = -1;
//    bt.SqBiTNode[6] = 80;
//    bt.SqBiTNode[7] = -1;
//    bt.SqBiTNode[8] = -1;
//    bt.SqBiTNode[9] = 27;

    //创建二叉树T2
    bt.ElemNum = 11;
    bt.SqBiTNode[0] = 40;
    bt.SqBiTNode[1] = 50;
    bt.SqBiTNode[2] = 60;
    bt.SqBiTNode[3] = -1;
    bt.SqBiTNode[4] = 30;
    bt.SqBiTNode[5] = -1;
    bt.SqBiTNode[6] = -1;
    bt.SqBiTNode[7] = -1;
    bt.SqBiTNode[8] = -1;
    bt.SqBiTNode[9] = -1;
    bt.SqBiTNode[10] = 35;

    //方法1
    //int val = -1;
    //std::string res = judgeInOrderBST(bt, 0, &val)?"是":"否";
    //方法2
    std::string res = judgeBST(bt)?"是":"否";
    std::cout<<"判断是否是二叉搜索树："<<res;
    return 0;
}