现代雷达车载应用——第2章汽车雷达系统原理 2.3节信号模型

经典著作，值得一读，英文原版下载链接【免费】ModernRadarforAutomotiveApplications资源-CSDN文库。

2.3 信号模型

雷达的发射机通常发出精心设计和定义明确的信号。然而，接收到的返回信号是多个分量的叠加，包括目标的反射、杂波、噪声，在某些情况下还有干扰。这些元素都不完全在雷达设计者的控制之下。雷达信号处理的最终目的是提取有关目标存在及其特征的有用信息。噪声和干扰的存在会降低测量目标特性的能力或精度。探测概率、信噪比（SNR）等各种性能指标可以用来评价雷达系统设计及其信号处理的有效性。

对于传统的连续波雷达，假设它发射一个设计良好的波形，其频率可以表示为f(t)，- T0 /2≤t < T0/2，其中T0为波形的持续时间。对于单音频信号，很容易知道：

(2.10)

这里fc是中心频率。

FMCW波性可以写作：

(2.11)

发射信号的瞬时相位φ(t)是f(t)的积分，

(2.12)

时域发射信号为

(2.13)

这里a(t)是发射信号的幅度，θ(t)是发射信号的额外相位。根据波形设计，a(t)和θ(t)可以是恒定值，也可以是时变调制。

接收到的信号是发射波形的延迟回波，其振幅和相位调制会因传输损耗和多普勒频移而改变。接收机噪声可以看作是一种加性随机信号。完整的接收信号可以建模为

(2.14)

这里ti = 2Ri/c是第i个反射波的往返时延，Ri是第i个反射波的距离，n(t)是接收机噪声，bi(t)是第i个反射器的幅度，ϕi(t)是第i个反射波的相位调制。y(t)中最重要的参数是时延ti，信号幅度bi(t)和相位调制ϕi(t)。目标距离能从ti估计。目标的尺寸决定信号幅度bi(t)，其运动状态随相位调制项ϕi(t)变化而变化。需要注意，i并不代表第i个目标。实际上，一个目标由多个反射面构成。

为了设计有效的信号处理算法，需要有良好的待处理信号模型。在本章中，将介绍几种雷达信号特性模型，以便更好地理解雷达测量。

2.3.1幅度模型

2.3.1.1点目标雷达距离方程

雷达距离方程是基础雷达系统设计分析中应用最广泛的工具之一。雷达距离方程描述了从发射机到接收机的电磁功率的物理依赖性。

为了推导距离方程，假设各向同性辐射元件将功率为Pt瓦特的波形传输到无损介质中。在R范围内的功率密度等于总功率Pt除以半径为R的球体的表面积，假设在介质中没有功率损失:

各向同性传输功率密度： (2.15)

对于汽车雷达来说，通常使用定向天线将电磁能量聚焦在感兴趣的角度上。天线增益Gt为最大功率密度与各向同性密度之比。因此，对于定向天线，距离R处的峰值功率密度为Gt乘以各向同性发射功率密度:

峰值传输功率密度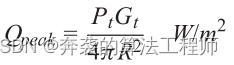： (2.16)

在距离R处有一个理想的点目标时，一部分电磁波向雷达接收机反向散射。图像表明，该点目标收集了面积为σ平方米的所有能量，并进行了各向同性的再辐射。总再辐射功率为

总再辐射功率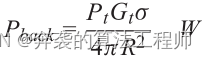： (2.17)

这个量σ称为目标的雷达截面(RCS)。RCS是衡量目标在雷达接收器方向上反射雷达信号的能力。它是雷达方向(从目标方向)的后向散射密度与被目标拦截的功率密度之比。因此，RCS通常不等于目标的物理横截面积。此外，在假设后向散射功率是各向同性再辐射的情况下，对RCS进行了定义。与式(2.15)类似，雷达接收机在距离R处的功率密度可以由式(2.17)的功率除以半径为R的球体表面得到，

后向散射功率密度： (2.18)

如果雷达接收机天线的孔径是Ae，接收机收到的所有后向散射功率为

接收功率： (2.19)

根据有效孔径大小的定义，有效孔径大小Ae和接收机天线增益的关系为

(2.20)

这里λ是波长。式(2.19)可以重新写作

(2.21)

它描述了一种理想的情况，即雷达的电磁波在大气中不会遭受任何额外的损失。此外，这里的雷达本身也是一个理想的系统，没有额外的组件损失或信号处理的增益。

雷达距离方程是雷达系统设计和分析的基本工具。例如，由式(2.21)可知，接收功率随着雷达与目标距离的四次方而减小。因此，为了增加给定RCS目标的探测距离，需要增加发射功率Pt或天线增益Gt, Gr。Pt Gt Gr增加约12 dB，只能使给定RCS目标的探测距离增加一倍。对雷达系统设计者来说，做出这样的改进总是具有挑战性的。

如上所述，(2.21)不包括信号处理带来的增益。设计良好的信号处理算法可以提高有效接收功率，例如提高信噪比，从而增加检测距离。信号处理的影响将在接下来的章节中讨论。

2.3.1.2雷达散射截面积

RCS的概念已经在上面直观地介绍过了，它代表了向雷达接收机再辐射的功率量。假设目标位置处的入射功率密度为Qpeak，如式2.16所示，距离R处雷达接收机处的再辐射功率密度为Qback，如式2.18所示。RCS σ是入射功率密度上面积的一部分。Qpeak、Qback和rcs之间的关系应满足:

(2.22)

假设后向散射功率密度来自于目标的各向同性辐射。因此，式(2.22)可以改写为:

(2.23)

RCS的定义通常用电场来表示。距离R趋于无穷大，使得定义只取决于目标的特性。

(2.24)

式中|Er |2和| Et |2分别为后向散射和入射电场的平方量级。RCS的典型值范围为0.01平方米到数百平方米。通常使用分贝(dBsm, dB平方米)表示RCS值:

(2.25)

上面定义的RCS是一个实数。RCS的一个更广义的定义是偏振散射矩阵(PSM) S，它描述了后向散射电磁场的极化状态。入射电磁场与后向散射电磁场之间的关系可以用PSM来描述:

(2.26)

其中下标H为水平极化，下标V为垂直极化。散射矩阵的四个元素是复杂的，可以由极化雷达的四个通道测量的幅度和相位得到。关于偏振技术的讨论超出了本书的范围。因此，在本书中，假设只发射一个固定偏振，接收一个固定偏振。

真实目标的RCS是射向角、频率和偏振的函数。它不能简单地用常数来表示。理论上，目标的RCS可以通过求解具有适当边界条件的麦克斯韦方程组来确定。但是，只有具有简单几何形状的对象才能以这种方式确定。一些简单对象的RCS近似公式如表2.3所示。

表2.3 简单物体RCS的近似形式[21]

大型复杂目标的RCS高度依赖于射向角和频率。图2.10是一个简单的三面体角反射镜的例子，其边长为a = 0.1 m。图2.11显示了当雷达正对着反射镜中心时其RCS与频率的关系。该反射器在10 GHz频率下的RCS为-3 dBsm，在77 GHz频率下的RCS为14 dBsm。

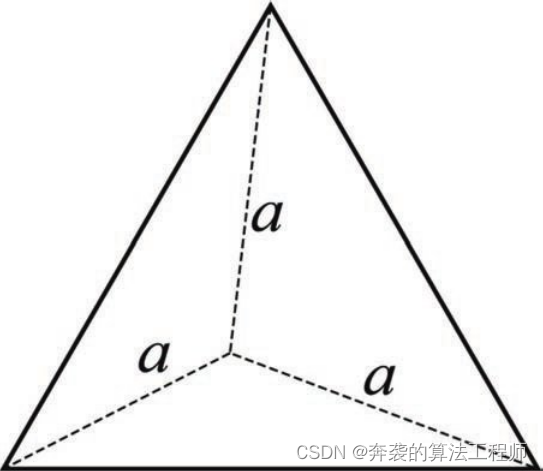
图2.10 三角反射器

图2.11 三角反射器的RCS和频率关系

观测角度是影响复杂目标RCS的另一个重要因素。如图2.12所示，同样的三面体反射镜，其RCS在反射镜中心观察时达到最大值，随着观察角度的变化而降低。当观察反射器的侧面时，RCS降低了70 dB以上。

图2.12 三角反射器的RCS在77GHz和观察角度关系

对于更复杂的目标，例如用于汽车应用的乘用车，其RCS从一个角度到另一个角度的变化更快。图2.13是乘用车在77 GHz下不同观测角度的RCS示例。0°表示从汽车前方观察，180°表示汽车后方。最大的RCS是90°，在车的侧面。

图2.13 在77GHz的乘用车的RCS

2.3.1.3 Swerling模型

上述雷达方程模型采用给定雷达RCS的空间单点目标进行基本分析。我们还讨论了除了简单的形状外，真实物体的RCS很难估计，如表2.3所示。在引入详细的计算机建模之前，现实世界对象的RCS通常是测量而不是计算的。然而，在受控环境中测量的RCS由于雷达信号在目标上多个点的反射而不能考虑到现实世界的影响。图2.14给出了一个客车的简单例子，它有两条反射路径r和r’。由于r和r’与雷达法线的相对角度，r和r’的差值会随着汽车距离的变化而变化。这导致接收到的信号被放大或减小取决于r和r’的差异。当目标相对于雷达移动时，这些距离改变并产生不断变化的信号。波动损失是雷达系统中目标物体相对于雷达系统移动或改变其方向所产生的一种效应。在20世纪50年代，Peter Swerling对其进行了广泛的研究，他引入了Swerling模型来模拟这种效应[22,23]。

图2.14 乘用车反射路径

Swerling目标模型将目标视为若干独立的辐射体，并使用卡方分布来考虑RCS σ

(2.27)

式中σmean为t的均值，Г(o/2)为伽马函数，I[0,∞)( σ)为第一类修正贝塞尔函数。o是自由度。卡方分布的标准差为2o，均值为o。标准差与均值之比等于1/o/2，这意味着较大的o值会导致较小的函数。如果o = ∞，则目标的RCS不起作用。

模型之间的差异很大程度上取决于自由度和目标的总体布局。Swerling的原始论文中考虑了Swerling I-IV模型。模型V，也称为0模型，是具有无限个自由度的简并情况，它表示一个无函数目标。

SwerlingⅠ

Swerling I描述了RCS根据两个自由度(o = 2)的卡方概率密度函数(pdf)变化的情况。这适用于由许多强度相似的独立反射器组成的目标。在该模型中，目标的速度相对于观测时间较低。RCS从一个脉冲到另一个脉冲是恒定的，但在不同的扫描之间是独立变化的。RCS的pdf被简化为瑞利函数:

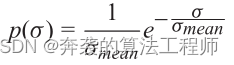(2.28)

Swerling Ⅱ

Swerling II模型与Swerling I模型相似，不同之处在于RCS值的变化更快，从脉冲到脉冲，而不是扫描到扫描。

Swerling III

Swerling III描述了RCS根据四个自由度(o = 4)的卡方pdf变化的情况。这适用于由许多独立反射体和一个大型主导反射体组成的目标。在该模型中，目标的速度相对于观测时间较低。RCS从脉冲到脉冲是恒定的，但在扫描到扫描之间独立变化。RCS的pdf为

(2.29)

Swerling IV

Swerling IV模型与Swerling III模型相似，只是RCS值的变化更快，从脉冲到脉冲，而不是扫描到扫描。

Swerling 0/ V

Swerling V(也称为Swerling 0)描述了一个常数RCS，对应于无限自由度(o = ∞)。

表2.4给出了从Swerling模型I到Swerling模型IV的Swerling目标模型的总结。对于汽车雷达应用，乘用车、卡车和摩托车通常被认为是Swerling III目标。骑自行车的人和行人通常被认为是Swerling I的目标。

2.3.2噪声模型

对于任何类型的接收机，噪声都是不可避免的。在雷达系统中，从目标接收到的回波信号需要与噪声竞争才能被识别。汽车雷达的噪声源包括接收机天线接收到的外部噪声，以及雷达接收机本身产生的内部噪声。

外部噪声可分为大气噪声、地外噪声和人为噪声。由自然大气过程引起的大气噪声，主要是雷暴中的闪电放电。这种噪声的能量通常在频谱上扩散。地外噪音包括宇宙和太阳噪音。人为噪音是指人类活动产生的噪音。

内部噪声包括热噪声、散弹噪声、隔层噪声和变频噪声。热噪声是由欧姆损耗引起的。散粒噪声是由电子或空穴随机到达晶体管的集电极或漏极而产生的。它也是由电子或空穴在PN结上的随机运动引起的。当电流必须在两条或多条路径之间进行分割时，就会产生分割噪声，这是分割过程中的随机函数的结果。闪烁噪声是一种功率谱密度为1/f的电子噪声，通常与直流(dc)有关，因为电阻函数根据欧姆定律转换为电压或电流函数[24]。

在上述各种噪声源中，热噪声通常占主导地位。热噪声可以近似为白噪声[25]。热噪声的功率谱Sn为

(2.30)