退役啦,接下来的博客全是图一乐啦
E - Joint Two Strings
题意
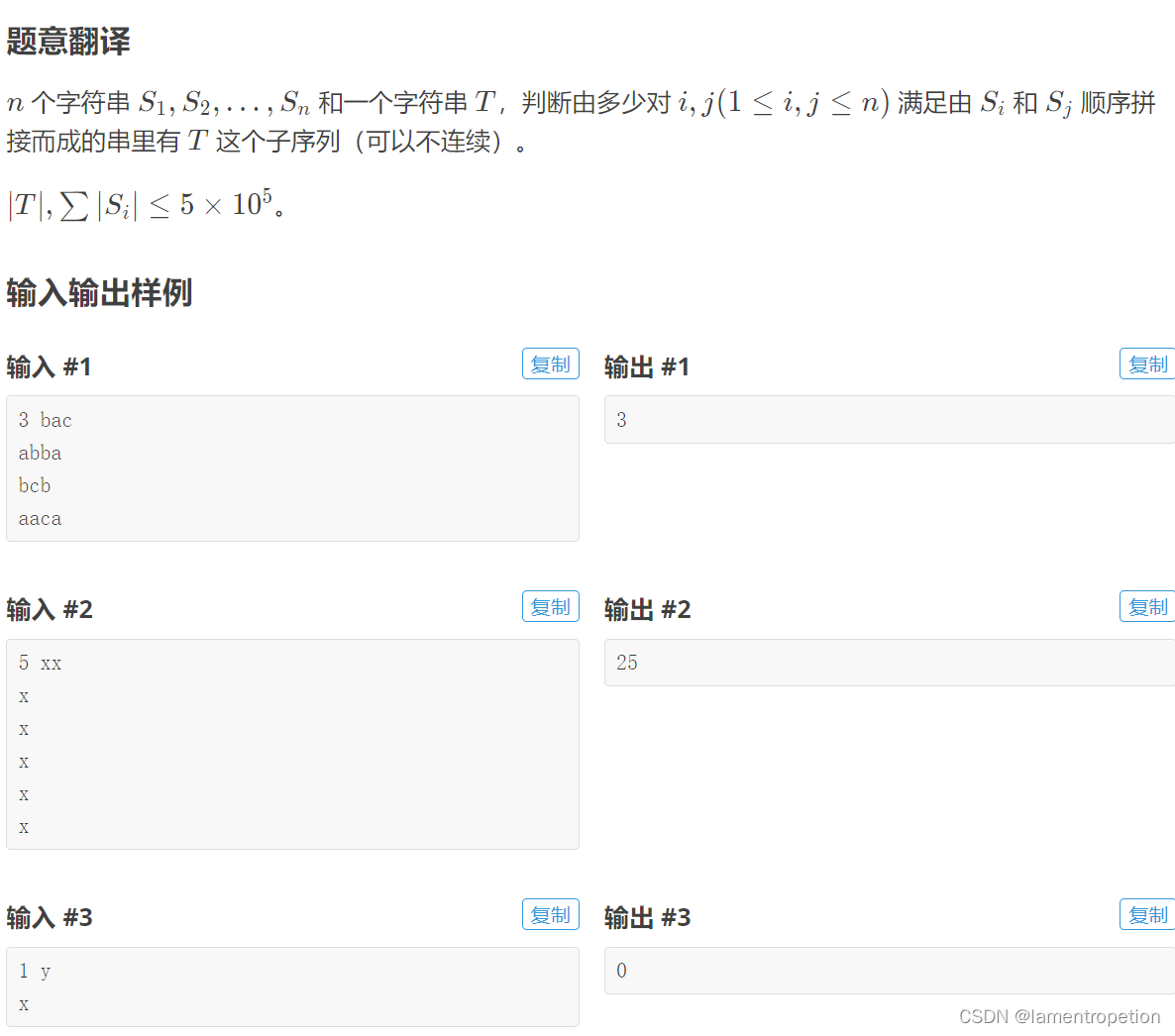
思路
统计两个指针的方案数一定是枚举一个,统计另一个
然后因为拼起来之后要包含 t 这个字符串,隐隐约约会感觉到和前缀后缀子序列有关
考虑预处理每个 s[i] 的最长公共前缀子序列 和 最长公共后缀子序列,接下来问题就变成:
满足ai + bj >= m有多少对 (i, j),这个直接值域统计一下即可
#include <bits/stdc++.h>
#define int long long
constexpr int N = 5e5 + 10;
constexpr int M = 1e4 + 10;
constexpr int mod = 1e9 + 7;
constexpr int Inf = 0x3f3f3f3f;
std::string t, s[N];
int n;
int pre[N], suf[N];
int mp[N];
void solve() {
std::cin >> n >> t;
int m = t.size();
t = " " + t;
for (int i = 1; i <= n; i ++) {
std::cin >> s[i];
s[i] = " " + s[i];
}
for (int i = 1; i <= n; i ++) {
int len = s[i].size() - 1;
pre[i] = 1;
for (int j = 1; j <= len; j ++) {
if (pre[i] <= m && t[pre[i]] == s[i][j]) {
pre[i] += 1;
}
}
pre[i] -= 1;
suf[i] = m;
for (int j = len; j >= 1; j --) {
if (suf[i] >= 1 && t[suf[i]] == s[i][j]) {
suf[i] -= 1;
}
}
suf[i] += 1;
mp[suf[i]] += 1;
}
for (int i = 2; i <= m + 1; i ++) {
mp[i] += mp[i - 1];
}
int ans = 0;
for (int i = 1; i <= n; i ++) {
ans += mp[pre[i] + 1];
}
std::cout << ans << "\n";
}
signed main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
int t = 1;
while(t --) {
solve();
}
return 0;
}