一、算法介绍

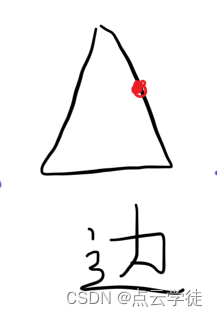
判断某一点是否在三角形的边上
之前已经介绍了点在三角形的内外判断方法，这里增加点恰好在三角形边上的判断方法
（本质上是遍历每条边，查看点是否在边上，所以对于多边形也是适用的。）

代码复制粘贴即可使用

二、算法实现

1.代码

#include <iostream>
using namespace std;

struct Point {
    float x, y;
};

// 判断点是否在三角形的某条边上
bool isOnTriangleEdge(Point p1, Point p2, Point p3, Point p) {
    float epsilon = 0.000001; // 用于比较浮点数的误差范围

    // 检查点p是否在边p1-p2上
    if (abs((p2.y - p1.y) * (p.x - p1.x) - (p.y - p1.y) * (p2.x - p1.x)) < epsilon) {
        if (p.x >= min(p1.x, p2.x) && p.x <= max(p1.x, p2.x) && p.y >= min(p1.y, p2.y) && p.y <= max(p1.y, p2.y)) {
            return true;
        }
    }

    // 检查点p是否在边p2-p3上
    if (abs((p3.y - p2.y) * (p.x - p2.x) - (p.y - p2.y) * (p3.x - p2.x)) < epsilon) {
        if (p.x >= min(p2.x, p3.x) && p.x <= max(p2.x, p3.x) && p.y >= min(p2.y, p3.y) && p.y <= max(p2.y, p3.y)) {
            return true;
        }
    }

    // 检查点p是否在边p3-p1上
    if (abs((p1.y - p3.y) * (p.x - p3.x) - (p.y - p3.y) * (p1.x - p3.x)) < epsilon) {
        if (p.x >= min(p1.x, p3.x) && p.x <= max(p1.x, p3.x) && p.y >= min(p1.y, p3.y) && p.y <= max(p1.y, p3.y)) {
            return true;
        }
    }

    return false;
}

int main() {
    Point p1 = { 0, 0 };
    Point p2 = { 4, 0 };
    Point p3 = { 2, 4 };
    Point p = { 2, 4 };

    if (isOnTriangleEdge(p1, p2, p3, p)) {
        cout << "点在三角形的边上" << endl;
    }
    else {
        cout << "点不在三角形的边上" << endl;
    }

    system("pause");
    return 0;
}

2.结果

---

总结

这个和之前判断内部还是外部的方法结合，即可完整表达点与三角形的相对位置关系