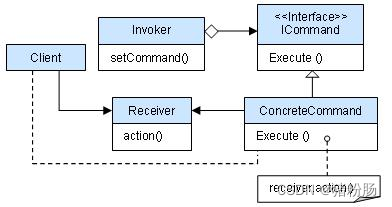
我们可以通过手头掌握的样本来估计总体的概率分布。这个过程由以下步骤组成。

第一步，我们采用Seaborn软件的histplot函数建立核密度图（一种概率密度图）。

import numpy as np
#输入样本数据
x=np.array([2.12906357, 0.72736725, 1.05152821, 0.48600398, 1.91963227,
        1.62165678, 8.86319952, 0.24399412, 4.19883103, 2.80846683,
        1.34644303, 0.35146917, 1.7575424 , 3.90572887, 1.07404978,
        4.05247124, 0.65839571, 0.40166037, 2.03241598, 0.53592929])
import seaborn as sns
#kde=True会绘制概率密度曲线，否则只有直方图
sns.histplot(x,kde=True)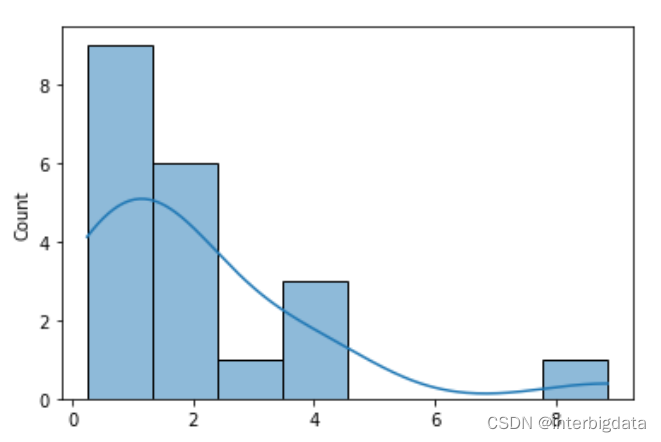

第二步，确定几个与之相近的候选概率分布（一般3个左右）。从上图来看，可以选择卡方分布、指数分布、伽玛分布。

第三步，分布拟合这三个候选分布的参数，并使用拟合得出的分布参数检验每一个候选分布

import scipy.stats as stats
#构造候选分布集合
dists={'expon':stats.expon,'chi2':stats.chi2,'gamma':stats.gamma}

for dist in dists:
    #拟合每一个分布
    params=dists[dist].fit(x)
    #检验每一个分布
    test=stats.kstest(x,dists[dist].cdf,params)
    print(dist,test.pvalue,params)

第四步，选择p值（每一个值）最大的作为检验结果

expon 0.9001 (0.016, 1.91)
chi2  0.3800 (1.78, 0.016, 1.37)
gamma 0.8080 (0.94, 0.016, 1.95)

 从以上数据可以看出，样本最大可能是参数的指数分布。而事实上，原始样本确实是以生成的随机数样本