题目链接

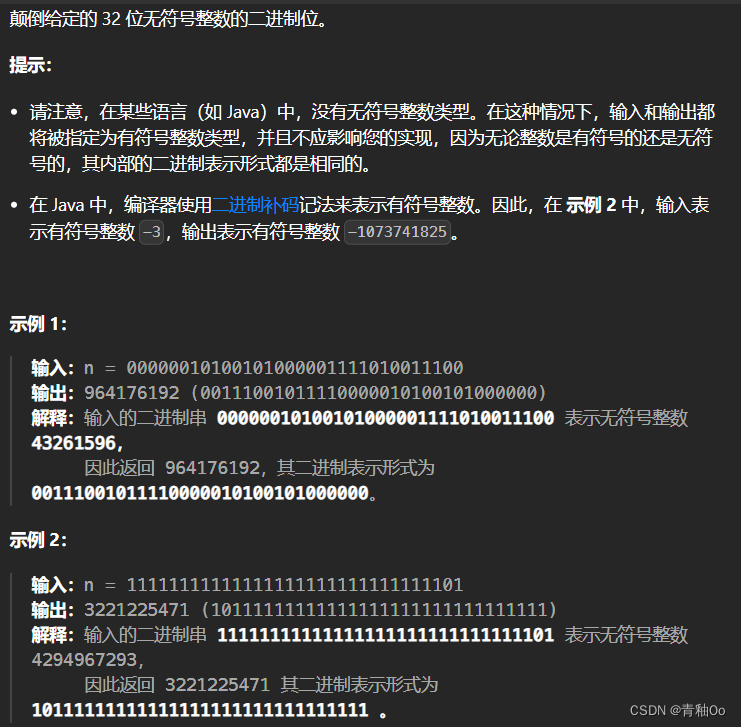
颠倒二进制位

题目描述

注意点

• 输入是一个长度为 32 的二进制字符串

解答思路

• 可以灵活运用位运算对二进制位进行颠倒，思路为：从后往前判断第i位是否为1，判断第i位是否为1可以将其二进制右移i位后与1进行&操作，如果为1说明其对颠倒后的第(32 - i)位产生了影响，将结果加上1的(31 - i)次方

代码

public class Solution {
    public int reverseBits(int n) {
        int res = 0;
        for (int i = 0; i < 32; i++) {
            // 从后往前判断任意每一位是否为1
            boolean isOne = ((n >> i) & 1) == 1;
            // 如果为0无变化，为1则需要将相应颠倒位置置为1
            if (isOne) {
                res += (1 << (31 - i));
            }
        }
        return res;
    }
}

关键点

• 灵活运用位运算