LeetCode题解二叉树（七）：222 完全二叉树的节点个数；110 平衡二叉树；257 二叉树的所有路径

news2024/9/28 9:24:24

前言

阳过之后，已经有一周多没有接触过一道题目了

从今日开始恢复每日一小时的刷题日常

二叉树

222 完全二叉树的节点个数 medium

无论是深度遍历（前中后都好）还是层序遍历，都可以用于求解这道题，只需要使用一个额外的变量记录访问到的结点数量就行。

这道题的考察点在于，如何利用完全二叉树的优势来求解这道题：

作为回归的第一道题目，我们都用一遍

如果是一棵普通的二叉树，那么递归法代码如下：

int getNum(TreeNode* cur) {
    if (!cur) return 0;
    int leftNum = getNum(cur->left);
    int rightNum = getNum(cur->right);

    return 1 + leftNum + rightNum; 
}

int countNodes(TreeNode* root) {
    if (!root) return 0;
    return getNum(root);
}

精简后代码如下：

int countNodes(TreeNode* root) {
    if (root == NULL) return 0;
    return 1 + countNodes(root->left) + countNodes(root->right);
}

时间复杂度：O(n)
空间复杂度：O(log n)，算上了递归系统栈占用的空间

而层序遍历代码如下：

int countNodes(TreeNode* root) {
    queue<TreeNode*> que;
    if (root) que.push(root);
    int res = 0;
    while (!que.empty()) {
        int size = que.size();
        for (int i = 0; i < size; i++) {
            TreeNode *cur = que.front();
            que.pop();
            res++;
            if (cur->left) que.push(cur->left);
            if (cur->right) que.push(cur->right);
        }
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(n)

接下来我们应当利用一下完全二叉树的特性来求解这道题

实际上，完全二叉树有两种，一种是满二叉树，另一种则是最后一层叶子结点并没有满

那么如何判断完全二叉树满不满，就成了求解这道问题的关键。

有一种方式，就是某结点向左递归的深度始终等于向右递归的深度，就可以断定该二叉树满

利用这个想法，代码如下：

int countNodes(TreeNode* root) {
    if (root == nullptr) return 0;
    TreeNode* left = root->left;
    TreeNode* right = root->right;
    // 这里初始为0是有目的的，为了下面求指数方便
    int leftDepth = 0, rightDepth = 0; 
    while (left) {  // 求左子树深度
        left = left->left;
        leftDepth++;
    }
    while (right) { // 求右子树深度
        right = right->right;
        rightDepth++;
    }
    if (leftDepth == rightDepth) {
        return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
    }
    return countNodes(root->left) + countNodes(root->right) + 1;
}

时间复杂度：O(log n × log n)
空间复杂度：O(log n)

110 平衡二叉树 easy

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。保持平衡的原因，也是为了在利用二叉树存储数据时，左右两边侧重不至于过于明显。

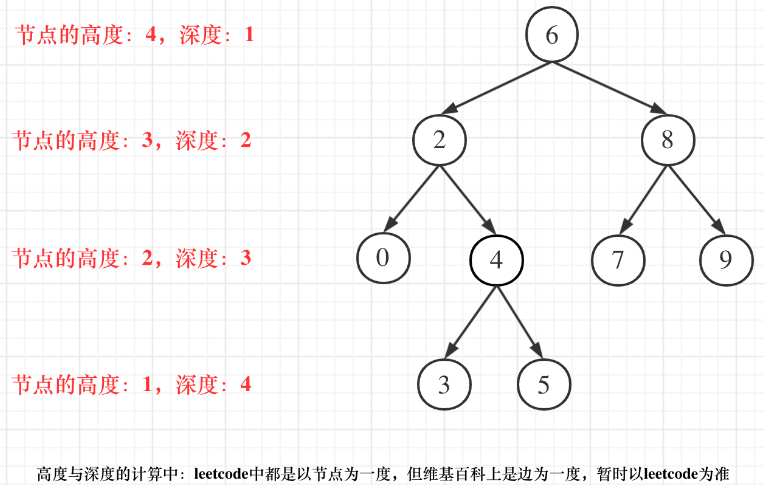
此处需要再强调一遍，求二叉树的深度，需要前序遍历（中左右），因为要从上而下的去查；

而求解深度，需要后序遍历（左右中），因为要从下而上的查。

递归法，需要递归的是左右子树的高度，最后要进行是否平衡的判断，代码如下：

int getHeight(TreeNode* node) {
    if (node == NULL) {
        return 0;
    }
    int leftHeight = getHeight(node->left);
    if (leftHeight == -1) return -1;
    int rightHeight = getHeight(node->right);
    if (rightHeight == -1) return -1;
    return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
    return getHeight(root) == -1 ? false : true;
}

迭代法代码如下（参考代码随想录）：

private:
    int getDepth(TreeNode* cur) {
        stack<TreeNode*> st;
        if (cur != NULL) st.push(cur);
        int depth = 0; // 记录深度
        int result = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);
                depth++;
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左

            } else {
                st.pop();
                node = st.top();
                st.pop();
                depth--;
            }
            result = result > depth ? result : depth;
        }
        return result;
    }

public:
    bool isBalanced(TreeNode* root) {
        stack<TreeNode*> st;
        if (root == NULL) return true;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();	// 中
            st.pop();
            if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {
                return false;
            }
            if (node->right) st.push(node->right);	// 右（空节点不入栈）
            if (node->left) st.push(node->left);	// 左（空节点不入栈）
        }
        return true;
    }

随想录中给出的说法如下：

当然此题用迭代法，其实效率很低，因为没有很好的模拟回溯的过程，所以迭代法有很多重复的计算。

虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。

例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！

因为对于回溯算法已经是非常复杂的递归了，如果再用迭代的话，就是自己给自己找麻烦，效率也并不一定高。

257 二叉树的所有路径 easy

本题初见回溯，但其实并不复杂，回溯的意思就是“倒回去”，回溯是一定要用递归的

递归的传入值，按照本题的要求来，必有的是结点，其次是一个用于存放路径值的数组，另一个则是存放最终结果的string数组；

终止条件也很简单，即遍历到叶子结点就可以结束了；

单层的处理逻辑，就要涉及到回溯的操作，即在遍历时弹出上一个遍历到的结点，此处附上精简后的代码：

void reversal(TreeNode* cur, string path, vector<string>& result) {
    path += to_string(cur->val); // 中
    if (cur->left == NULL && cur->right == NULL) {
        result.push_back(path);
        return;
    }
    if (cur->left) reversal(cur->left, path + "->", result); // 左
    if (cur->right) reversal(cur->right, path + "->", result); // 右
}

vector<string> binaryTreePaths(TreeNode* root) {
    vector<string> result;
    string path;
    if (root == NULL) return result;
    reversal(root, path, result);
    return result;

}

回溯的操作，用在了reversal(cur->left, path + "->", result)中的path + "->",每次函数调用完，实际上path是没有加上"->"的，这就相当于回溯了。

如果要用明白显眼的回溯逻辑，就是如下这样：

if (cur->left) {
    path += "->";
    traversal(cur->left, path, result); // 左
    path.pop_back(); // 回溯 '>'
    path.pop_back(); // 回溯 '-'
}
if (cur->right) {
    path += "->";
    traversal(cur->right, path, result); // 右
    path.pop_back(); // 回溯 '>' 
    path.pop_back(); //  回溯 '-' 
}

本题还有迭代的写法，具体如下：

vector<string> binaryTreePaths(TreeNode* root) {
    stack<TreeNode*> treeSt;// 保存树的遍历节点
    stack<string> pathSt;   // 保存遍历路径的节点
    vector<string> result;  // 保存最终路径集合
    if (root == NULL) return result;
    treeSt.push(root);
    pathSt.push(to_string(root->val));
    while (!treeSt.empty()) {
        TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
        string path = pathSt.top();pathSt.pop();    // 取出该节点对应的路径
        if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
            result.push_back(path);
        }
        if (node->right) { // 右
            treeSt.push(node->right);
            pathSt.push(path + "->" + to_string(node->right->val));
        }
        if (node->left) { // 左
            treeSt.push(node->left);
            pathSt.push(path + "->" + to_string(node->left->val));
        }
    }
    return result;
}