KL散度

直观理解：KL散度是一种衡量两个分布之间匹配程度的方法。通常在概率和统计中，我们会用更简单的近似分布来代替观察到的数据或复杂的分布，KL散度帮我们衡量在选择近似值时损失了多少信息。

在信息论或概率论中，KL散度（Kullback–Leibler divergence），又称为相对熵（relative entropy），是一种描述两个概率分布P和Q差异的一种方法。它是非对称的，这意味着D(P||Q)≠D(Q||P)。特别的，在信息论中，D(P||Q)表示当用概率分布Q来拟合真实分布P时，产生的信息损耗，其中Q表示真实分布，Q表示P的拟合分布。

对一个离散随机变量或连续随机变量的两个概率分布P和Q来说KL散度的定义分别如下所示

$D(P||Q) = ${\sum }_{i\in X}P(i)\ast [log(\frac{P(i)}{Q(i)})]$
$D(P||Q) = ${\int }_{x}P(x)\ast [log(\frac{P(i)}{Q(i)})]dx$

但似乎还是有点难以理解为什么KL散度就可以衡量两个分布之间的匹配程度了，下面举例说明。

举例探索

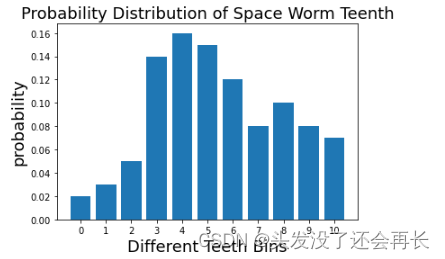
假设我们是一组正在广袤无垠的太空中进行研究的科学家。我们发现了一些太空蠕虫，这些太空蠕虫的牙齿数量各不相同，在收集和许多样本后，我们得出了蠕虫牙齿数量的经验概率分布，用数组表示true_data=[0.02, 0.03, 0.05, 0.14, 0.16, 0.15, 0.12, 0.08, 0.1, 0.08, 0.07]。现在我们需要将这些信息发回地球。但从太空向地球发送信息的成本很高，所以我们需要用尽量少的数据表达这些信息。我们有个好方法：我们不发送单个数值，而是绘制一张图表。这样就将数据转化为分布。
可视化如下：

true_data=[0.02, 0.03, 0.05, 0.14, 0.16, 0.15, 0.12, 0.08, 0.1, 0.08, 0.07]
assert sum(true_data)==1.0

pylab.bar(np.arange(len(true_data)), true_data)
pylab.xlabel('Different Teeth Bins', fontsize=18)
pylab.title('Probability Distribution of Space Worm Teenth', fontsize=18)
pylab.ylabel("probability", fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.show()

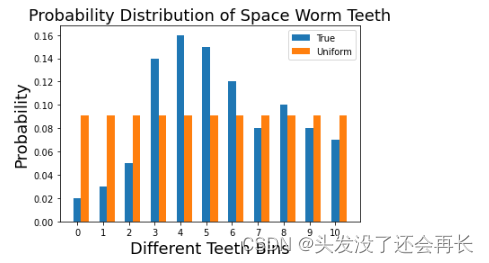
简化尝试：均匀分布（Uniform distribution）

这些数据很好，但是我们想更加简化这些数据，第一个选择是均匀分布。上面的概率数据转化为均匀分布。一共11个样本，所以每一个牙齿数量的概率都是1/11。

def get_unif_probability(n):
    return 1.0/n

unif_data = [get_unif_probability(11) for _ in range(11)]
width=0.3

pylab.bar(np.arange(len(true_data)),true_data,width=width,label='True')
pylab.bar(np.arange(len(true_data))+width,unif_data,width=width,label='Uniform')
pylab.xlabel('Different Teeth Bins',fontsize=18)
pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
pylab.ylabel('Probability',fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.legend()
pylab.show()

简化尝试：二项分布（binomial distribution）

显然我们的数据不是均匀分布的，现在尝试另一种二项分布对数据进行建模。我们需要计算二项分布的概率参数p，本例中n=10，E(X)=5.7，由E(X)=np得到p=0.57。则对于每一类牙齿个数的概率可以使用以下公式计算：
$P(X=i)=C_n^k{p}^k(1-p{)}^{(n-k)}$ i=(1,2,…)

def get_bino_probability(mean,k,n):
    return (factorial(n)/(factorial(k)*factorial(n-k)))*(mean**k)*((1.0-mean)**(n-k))

def get_bino_success(true_data,n):
    return np.sum(np.array(true_data)*np.arange(len(true_data)))/10.0

n_trials = 10
succ = get_bino_success(true_data,n_trials)
print('Success probability: ',succ)

bino_data = [get_bino_probability(succ,k,n_trials) for k in range(11)]

width=0.3

pylab.bar(np.arange(len(true_data)),true_data,width=width,label='True')
pylab.bar(np.arange(len(true_data))+width,bino_data,width=width,label='Binomial')
pylab.xlabel('Different Teeth Bins',fontsize=18)
pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
pylab.ylabel('Probability',fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.legend()
pylab.show()

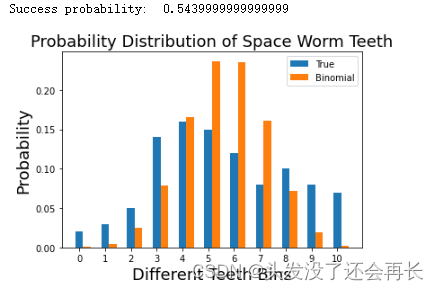
汇总分析

现在我们使用了两个分布去近似我们原始的概率分布，将它们绘制在同一个图中进行比较，如下图所示：

pylab.bar(np.arange(len(true_data))-width,true_data,width=width,label='True')
pylab.bar(np.arange(len(true_data)),unif_data,width=width,label='Uniform')
pylab.bar(np.arange(len(true_data))+width,bino_data,width=width,label='Binomial')
pylab.xlabel('Different Teeth Bins',fontsize=18)
pylab.title('Probability Distribution of Space Worm Teeth',fontsize=18)
pylab.ylabel('Probability',fontsize=18)
pylab.xticks(np.arange(len(true_data)))
pylab.legend()
pylab.show()

可以看到这两个分布都没有很好的近似我们的原始数据，但是我们需要衡量一下哪个更好。
我们最开始关注的就是如何使发送的信息最少，两个方法都减少了参数量，我们可以看哪个携带了更多的信息，这就是KL散度的作用。

熵

KL起源于信息论，信息论的主要目标是量化数据中有多少信息。某个信息$x_i$出现的不确定的大小定义为$x_i$所携带的信息量，用$I(x_i)$表示，$I(x_i)$与信息$x_i$出现的概率$p(x_i)$之间的关系为：
$I(x_i)=log\frac{1}{p(x_i)}=-logp(x_i)$
信息论中最重要的指标称为熵，通常表示为H。概率分布的熵的定义时：
$H=-{\sum }_{i=1}^{N}p(x_i)logp(x_i)$

如果我们在计算中使用2为底的对数，我们可以将熵解释为“编码所需的最小比特数”。在这种情况下，信息是指根据我们的经验分布给出的每个牙齿计数观察。根据我们观察到的数据，我们的概率分布的熵为3.12比特。比特数告诉我们，在平均情况下，我们需要多少比特来编码我们在单个情况下观察到的牙齿数量的下限。

但是，熵并不能告诉我们最佳的编码方案，以帮助我们实现这种压缩。最优编码是一个非常有趣的话题，但对于理解KL散度并不是必要的。熵的关键是，仅仅知道我们需要的比特数的理论下限，我们有一种方法来准确量化数据中包含的信息量。 现在我们可以量化这一点，我们想要量化的是当我们用参数化的近似替代我们观察到的分布时丢失了多少信息。

使用KL散度测量丢失的信息

Kullback-Leibler散度只是对我们的熵公式的略微修改。不仅仅是有我们的概率分布p，还有上近似分布q。然后，我们查看每个log值的差异：
$D(p||q) = ${\sum }_{i\in X}p(i)\ast [log(\frac{p(i)}{q(i)})]$
利用KL散度，我们可以精确地计算出当我们近似一个分布与另一个分布时损失了多少信息。让我们回到我们的数据，看看结果如何。

比较我们的近似分布

def get_klpq_div(p_probs, q_probs):
    kl_div = 0.0
    for pi, qi in zip(p_probs, q_probs):
        kl_div += pi*np.log(pi/qi)
    return kl_div

def get_klqp_div(p_probs, q_probs):
    kl_div = 0.0
    
    for pi, qi in zip(p_probs, q_probs):
        kl_div += qi*np.log(qi/pi)
        
print('KL(True||Uniform): ',get_klpq_div(true_data,unif_data))
print('KL(True||Binomial): ',get_klpq_div(true_data,bino_data))

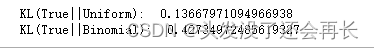
从计算的KL结果来看，使用二项分布损失的信息大于使用均匀分布损失的信息，所以我们最后如果从中选择一个，还是会选择均匀分布。

参考文章：
Kullback-Leibler(KL)散度介绍
KL散度代码地址