学习树状数组必不可少学习树状数组的精髓,lowbit()运算
在计算机中存储一个正数是以二进制的形式,而存储一个负数则是以二进制补码的形式,简单说就是二进制取反+1,lowbit运算就是提取出最后一个1以后的位置,比如10100进行lowbit运算就是100,11010进行lowbit运算就是10,在写的时候lowbit就是x&(-x),可以随便造几个数来看一下效果,假设x的二进制是10100,x的反码就是01011,加1以后就是01100,x&(-x)=100,这显然不是巧合。
而树状数组就是通过lowbit运算来存储前缀和,当然lowbit运算中不能有0的存在
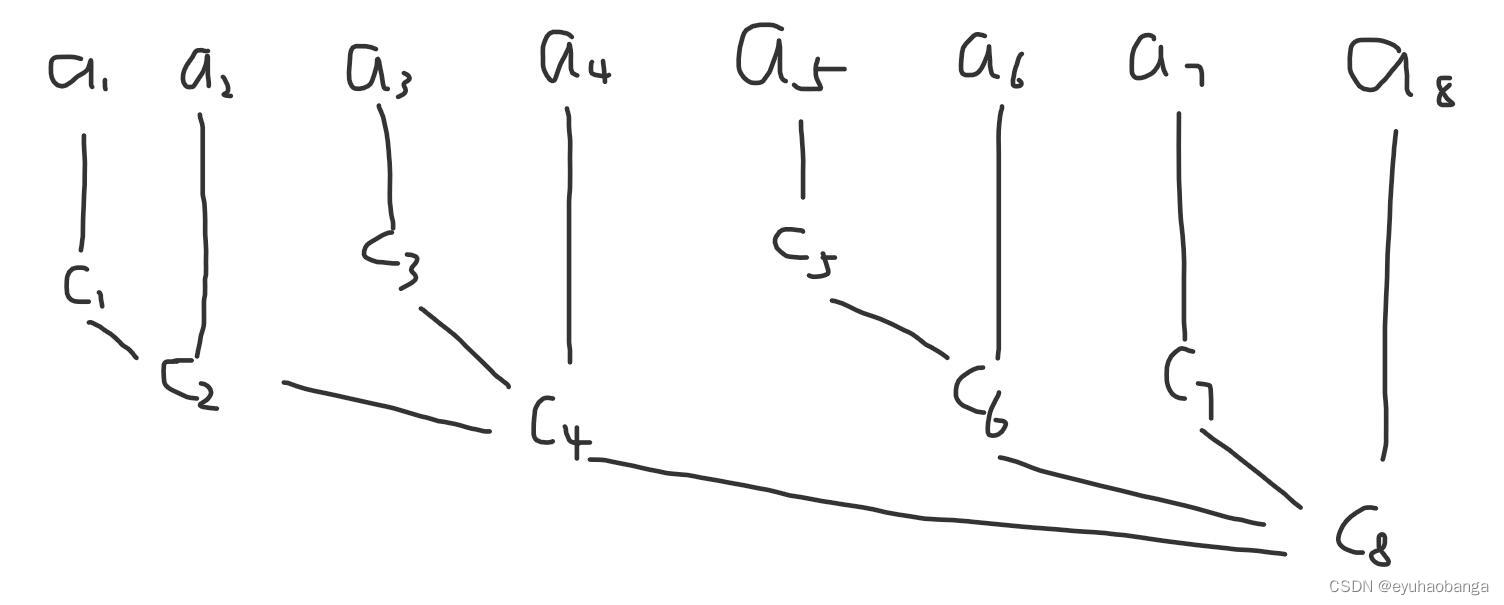
如图
在树状数组中,c[i]记录的是从i-lowbit(i)+1到i的和,因此单点修改,区间查询就是更改单点开始的所有lowbit即可,查询区间也是查询所有的lowbit,一维二维同理,二维就是循环两层
如果是区间修改,区间查询,可以借助一个新的差分数组d,可知d[1]=a[1],d[2]=a[2]-a[1],d[3]=a[3]-a[2],这里要求的是a数组的前缀和,那么a[1]=d[1],a[2]=d[1]+d[2],a[3]=d[1]+d[2]+d[3]...a数组前缀和就是a[1]=d[1],a[1]+a[2]=2*d[1]+d[2],a[1]+a[2]+a[3]=3*d[1]+2*d[2]+d[3]...通过归纳可以发现a[1~x]的和就等于
也就是
从这就能看出,树状数组此时需要维护两个区间,一个是差分数组d,一个是i*d
一些树状数组模板+模板题:
一维二维树状数组模板题加题解
一维二维树状数组模板(进阶版)
难点-树状数组
树状数组求逆序数
浅谈树状数组
news2026/2/12 8:51:56
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/130563.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
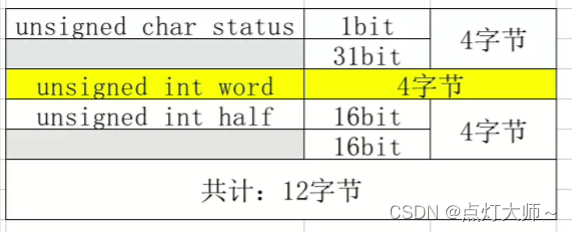
【C语言】结构体、共用体、位域
结构体
1、 结构体的声明方法 struct struct_name {data_type member1;data_type member2;..
};这是其中一种声明方式~ 2、定义一个结构体变量 struct struct_name variable;3、访问成员变量 . 运算
一个结构体变量访问其成员时,使用的是 . 运算
下面…
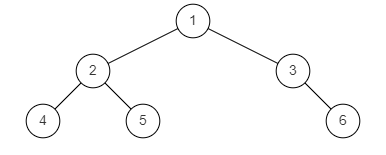
BM35 判断是不是完全二叉树
题目
给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为 h,除第 h 层外,其它各层的结点数都达到最大个数,第 h 层所有的叶子结点都连续集中在最左边,这就是完全二叉树。&a…
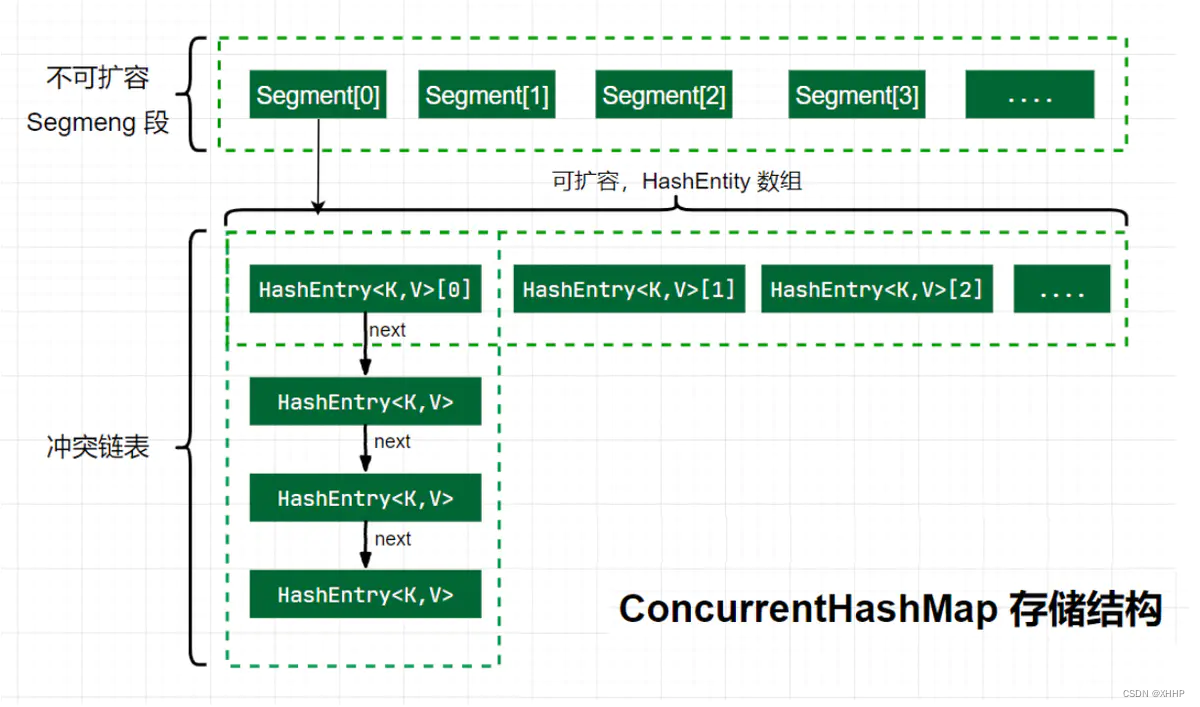
深入理解ConcurrentHashMap1.7源码
1. 概述
HashMap在我们的日常生活中使用很多,但是它不是线程安全的。我们可以使用HashTable来代替,主要实现方式是在方法中加入synchronized,所以效率也比较低。因此,对于键值对,我们可以尝试使用ConcurrentHashMap来…
实验室规划设计方案SICOLAB
一、实验室规划设计
喜格提供实验室布局方案
根据实验室性质、实验室定位、实验室功能、实验类型、实验工艺流程以及国家相关标准合理的规划布局。
喜格提供仪器摆放布局方案
根据该实验流程来确定仪器的种类、数量、规格型号、外形尺寸、电压功率等参数以及摆放位置以及提…
【Linux】tee、tail、killall、|、||、、命令学习
|、||、&、&&辨析
竖线‘|’在linux中是管道符的意思,将‘|’前面命令的输出作为’|后面的输入;
双竖线‘||’,用双竖线‘||’分割的多条命令,执行的时候遵循如下规则:如果前一条命令为真,则…
还在喷农民歌唱家大衣哥吗?他的一个不经意间的举动却造福了乡里
农民歌唱家大衣哥,一直以来都饱受争议,有人说他是炒货专家,然而事实真的如此吗?事实上,大衣哥也做了很多好事,像修桥补路等都不说了,单就他的一个不经意间的举动,就造福了四乡八邻。…
Windows内核--CPU和内核(1.7)
Windows内核支援哪些CPU? Intel x86/x86_64 IA64已不再支持. AMD amd64 ARM (Windows On Arm: WOA) ARM具备低功耗优势, 除了高通, 还有Broadcom/NXP等都支援ARM架构. 苹果自研M系列开了头,ARM不仅有低功耗,同样有性能,Windows也想分一杯羹…
【vue系列-03】vue的计算属性,列表,监视属性及原理
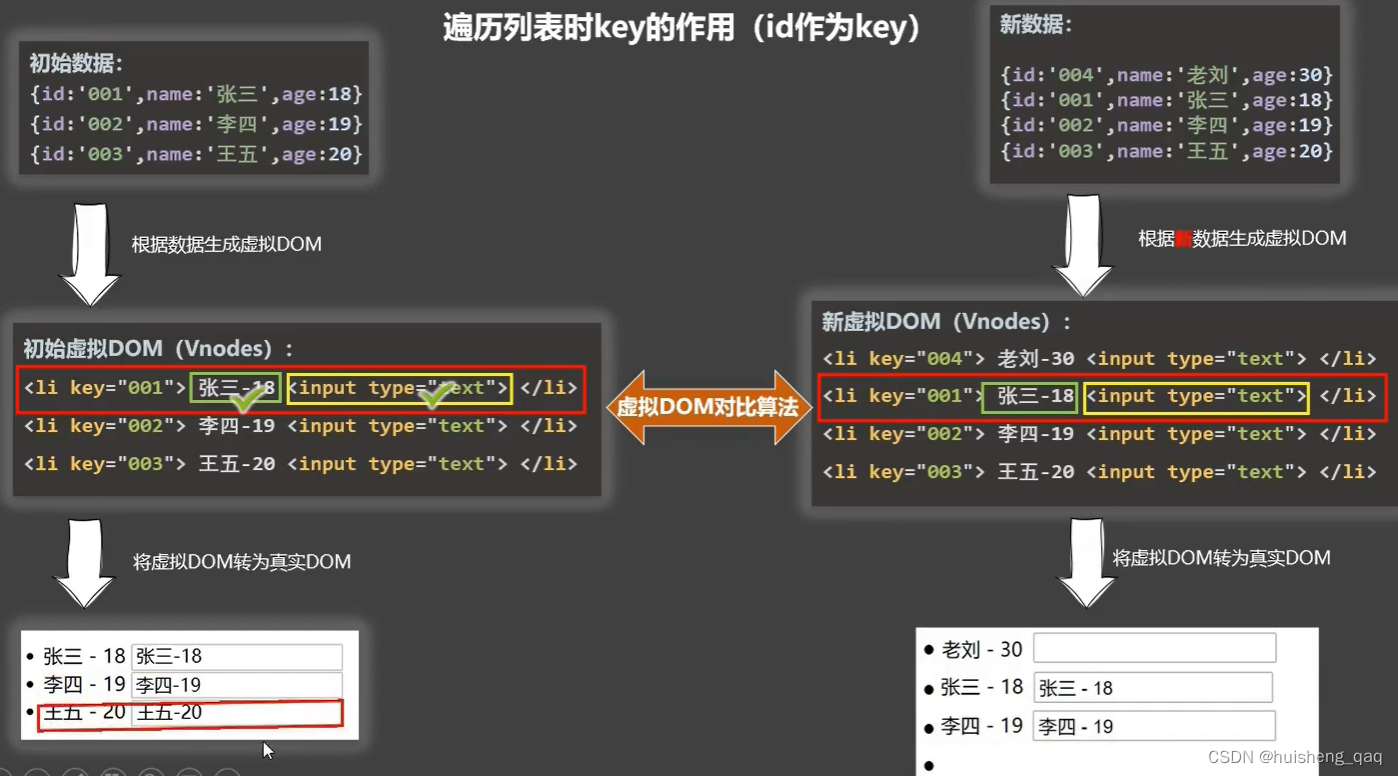
vue的核心属性一,vue核心属性1,计算属性2,监视属性3,样式绑定3.1,class样式绑定3.2,style样式绑定4,条件渲染5,列表渲染5.1,遍历列表5.2,key的作用5.3&#x…
2022年全国职业院校技能大赛中职组网络安全竞赛——隐写术应用解析(超详细)
2022年全国职业院校技能大赛中职组网络安全竞赛——隐写术应用解析(超详细) B-8任务八:隐写术应用 *任务说明:仅能获取Server8的IP地址 环境需求私信博主 1.找出文件夹1中的文件,将文件中的隐藏信息作为Flag值提交; 解题步骤如下 2.找出文件夹2中的文件,将文件中的隐藏信息…
基于Vue的数据可视化设计框架,数据大屏可视化编辑器
开发文档(★★★★★)
请访问 https://lizhensheng.github.io/vue-data-view/
完整代码下载地址:基于Vue的数据可视化设计框架,数据大屏可视化编辑器
简介
DataView是一个基于Vue的数据可视化设计框架提供用于可拖拽的控件提供…
Spring之IOC入门案例
目录
一:IOC入门案例实现思路分析
1.IOC容器管理什么?
2. 如何将被管理的对象告知 IOC 容器 ?
3.被管理的对象交给 IOC 容器,要想从容器中获取对象,就先得思考如何获取到 IOC 容器 ?
4.IOC 容器得到后,如何从容…
Android---开发笔记
ListView控件
<ListViewandroid:id"id/main_iv"android:layout_width"match_parent"android:layout_height"match_parent"android:layout_below"id/main_top_layout"android:padding"10dp"android:divider"null&qu…
JavaScript对象与类的创建
1、面向过程与面向对象
面向过程就是分析出解决问题所需要的步骤,然后用函数把这些步骤一步一步实现,使用的时候再一个一个的依次调用就可以了。面向对象是把事务分解成为一个个对象,然后由对象之间分工与合作。
面向过程与面向对象对比
面…
LeetCode11.盛水最多的容器
11. 盛最多水的容器
该题用的是贪心的思想,也即每一步都以更加靠近最值为目标,用双指针维护height数组,接下来我用我自己通俗的语言尽可能解释双指针这种做法的正确性:
首先双指针指向数组两端,从两端开始࿰…
必看!Salesforce发布2023年全球科技重要趋势和预测
Salesforce领导者处于影响企业的最新趋势、技术和挑战的前线,通过市场分析、客户对话等方面带来专业知识和洞察力。距离2023年还剩不到一周的时间,未来一年企业应该如何布局,技术会如何发展,值得我们密切关注。
企业需要了解的5项…
IB分数如何影响您的大学申请?
参加 2022 年 11 月 IB 考试的学生将于 1 月 2 日收到IBDP&IBDP相关课程的分数。
大多数在新加坡提供 IB 课程的国际学校都在每年 5 月参加考试。
但是有些学校在 11 月参加 IBDP 考试。其中包括圣约瑟国际学院(SJII)、英华学校(ACS)、澳大利亚国际学校(SAIS)、华中国际学校…
牛客竞赛每日俩题 - 动态规划3
目录
类01背包问题,选or不选
变种走方格 类01背包问题,选or不选
不同的子序列_牛客题霸_牛客网 问题翻译: S有多少个不同的子串与T相同 S[1:m]中的子串与T[1:n]相同的个数 由S的前m个字符组成的子串与T的前n个字符相同的个数 状态…