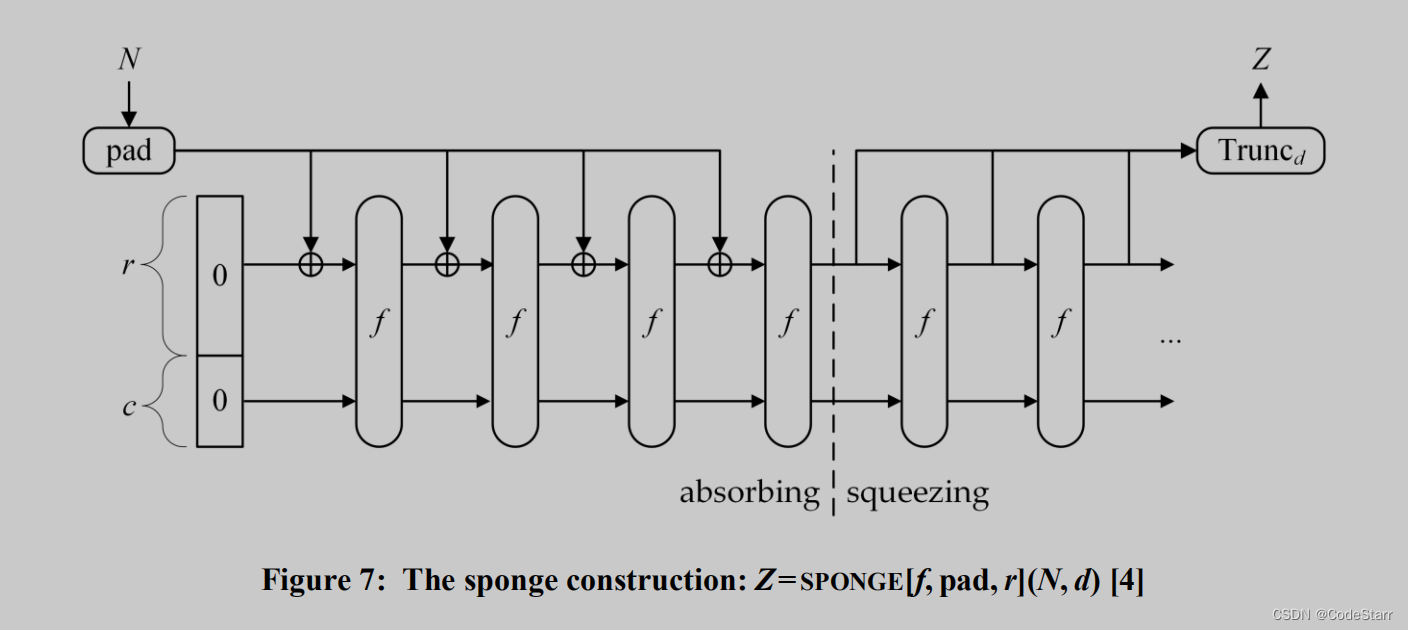
题目

给定一个二叉树，确定他是否是一个完全二叉树。

完全二叉树的定义：若二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的叶子结点都连续集中在最左边，这就是完全二叉树。（第 h 层可能包含 [1~2h] 个节点）

数据范围：节点数满足 1≤n≤100

样例图1：

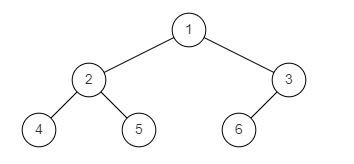
样例图2：

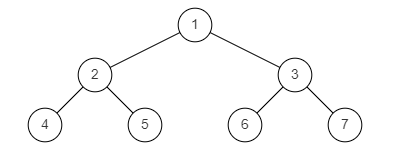
样例图3：

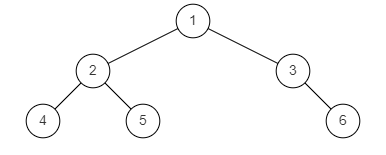
示例1

输入：{1,2,3,4,5,6}

返回值：true

示例2

输入：{1,2,3,4,5,6,7}

返回值：true

示例3

输入：{1,2,3,4,5,#,6}

返回值：false

---

思路

通过层序遍历来进行判断。

引入标志位isSecondStep，来区分当前遍历处在第一状态(isSecondStep==false)还是第二状态(isSecondStep==true)。

第一状态：

1. 当前节点cur的左右子树都存在；
2. 当前节点cur只有右树没有左树，是反例；
3. 当前节点cur只有左树没有右树（cur是第一个碰到的只有左树没有右树的节点），需要切换为第二状态；
4. 当前节点cur没有左树也没有右树（cur是第一个碰到的叶子节点），需要切换为第二状态。

第二状态：

1. 第二状态中所有节点不可能有子树，有一个就是反例。

---

代码

import java.util.*;

public class Solution {
    public boolean isCompleteTree (TreeNode root) {
        if(root == null) {
            return true;
        }

        //层序遍历判断二叉树
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        //引入标志位，来区分当前遍历过程中处在第一阶段还是第二阶段
        //false是第一阶段；true是第二阶段
        boolean isSecondStep = false;

        while(!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if(!isSecondStep) {
                //此时处在第一阶段
                if(cur.left != null && cur.right != null) {
                    //当前cur左右子树全部都存在
                    queue.offer(cur.left);
                    queue.offer(cur.right);
                } else if(cur.left == null && cur.right != null) {
                    //此时只有右树没有左树,反例
                    return false;
                } else if(cur.left != null) {
                    //只有左树没有右树，此时cur是碰到的第一个只有左树的节点，切换状态
                    isSecondStep = true;
                    queue.offer(cur.left);
                } else {
                    //此时左树和右树全部为空，cur是第一个碰到的叶子节点
                    isSecondStep = true;
                }
            } else {
                //此时处在第二阶段，第二阶段中所有节点不可能有子树
                if(cur.left != null || cur.right != null) {
                    return false;
                }
            }
        }
        //遍历全结束，没有找到反例
        return true;
    }
}