文章目录
- 1 INTRODUCTION
- 2 GLOSSARY
- 3 KECCAK-p Permutations
- 3.1 State
- 3.1.2 Converting Strings to State Arrays
- 3.1.3 Converting State Arrays to Strings
- 3.1.4 Labeling Convention for the State Array
- 3.2 Step Mappings
- theta
- rho
- pi
- chi
- iota
- 3.3 KECCAK-p[b, n~r~]
- 3.4 KECCAK-f
- 4 SPONGE CONSTRUCTION
- 5.1 Specification of pad10*1
- 5.2 Specification of KECCAK[c]
- 6 SHA-3 FUNCTION SPECIFICATIONS
- 6.1 SHA-3 Hash Functions
- 6.2 SHA-3 Extendable-Output Functions
- 6.3 Alternate Definitions of SHA-3 Extendable-Output Functions
- A Security
- A.1 Summary
- B Examples
- B.1 Conversion Functions
- B.2 Hexadecimal Form of Padding Bits
- 实现
- 参考资料
原文档: SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions,《SHA-3标准:基于置换的哈希与可扩展输出函数》
1 INTRODUCTION
2012年10月,NIST选用Keccak作为SHA-3的标准算法,经过对原算法的修改,于2015年8月发布标准文档FIPS 202,作为对FIPS 180-4 SHA-2的补充。
准确地说,Keccak团队当初提交的是Keccak-f[1600]。
SHA-3 family:
- 4 cryptographic hash functions:
- SHA3-224
- SHA3-256
- SHA3-384
- SHA3-512
- 2 eXtendable-Output Functions (XOFs):
- SHAKE128 (Secure Hash Algorithm KECCAK)
- SHAKE256
其中,XOF输出的哈希值可以任意指定长度。
消息后面会追加2 bits,用来区分hash函数和XOFs,或者以后的sha3变体。
2 GLOSSARY
3 KECCAK-p Permutations
2 parameters:
- b, in
{25, 50, 100, 200, 400, 800, 1600}: the fixed length of the strings that are permuted, called the width of the permutation. - nr, any positive integer: the number of iterations of an internal transformation, called a round.
表示:KECCAK-p[b, nr]
b取值25和50仅仅用于研究原理,不可实际应用。
3.1 State
对于KECCAK-p[b, nr] permutation, state表示b bits.
另外两个参数:
- w = b/25
- l = log2(b/25) = log2w
| b | 25 | 50 | 100 | 200 | 400 | 800 | 1600 |
|---|---|---|---|---|---|---|---|
| w | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| l | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
比特流state(S)也可以表示为 5x5xW的三维bit数组A[x][y][z](0≤x<5, 0≤y<5, and 0≤z<w),这里还涉及以下概念:
- 二维:sheets, planes, and slices
- 一维:rows, columns, and lanes.
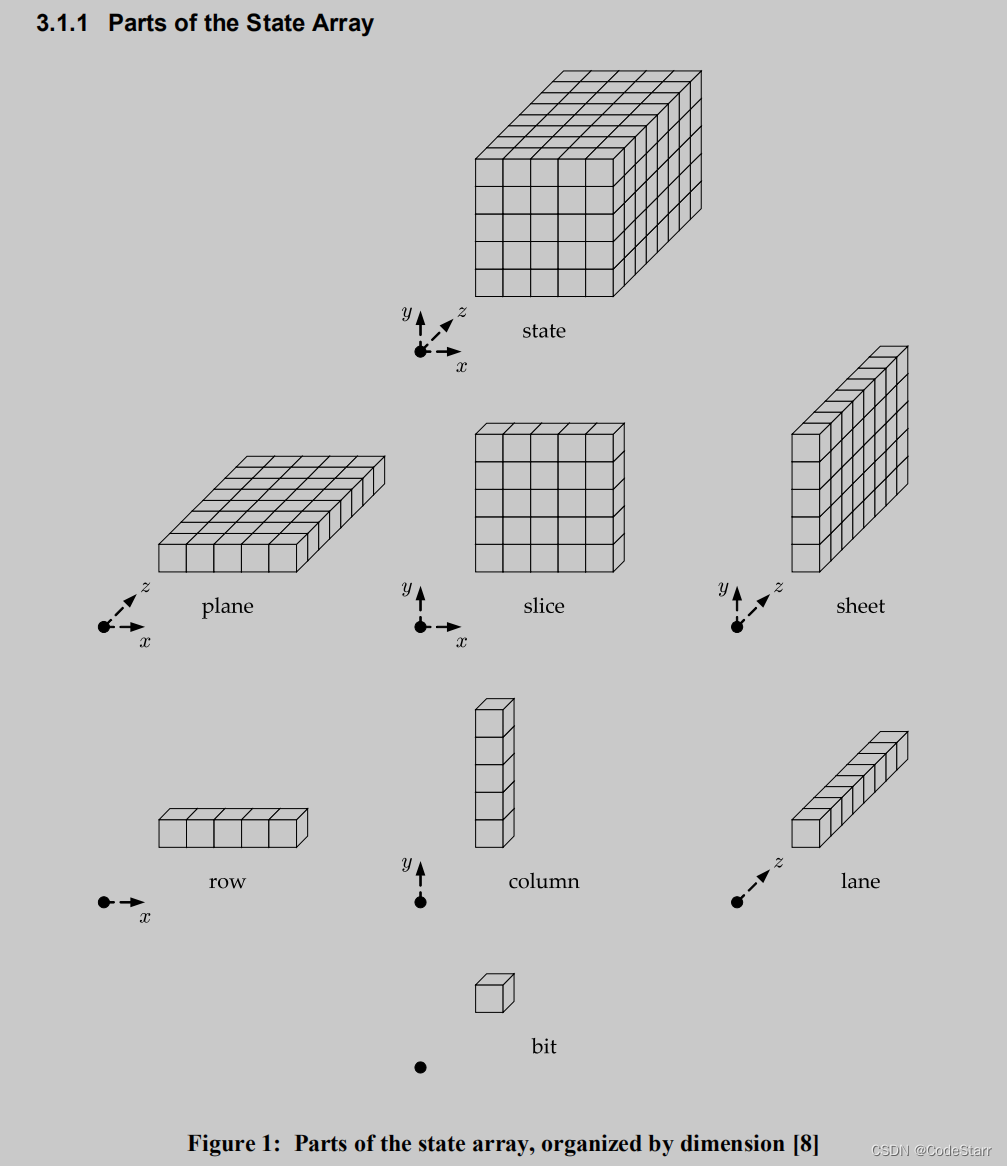
3.1.2 Converting Strings to State Arrays
A[x,y,z] = S[w(5y+x)+z]
其实就是点线面体,顺序为:
- lane ,z线
- plane ,xz面
- state,垒高
eg. b=1600, w=64
A[4,2,63]=S[959]
3.1.3 Converting State Arrays to Strings
其实就是反过来的过程,以lane为单位,从左到右,从下往上。
还是以b=1600, w=64为例:
S = A[0, 0, 0] || A[0, 0, 1] || ... || A[0, 0, 63]
|| A[1, 0, 0] || ... || A[1, 0, 63]
|| A[4, 4, 0] || ... || A[4, 4, 63]
3.1.4 Labeling Convention for the State Array
Z坐标为0的第一个slice面的中心为state原点。
X和Y轴坐标为3,4,0,1,2,也就是说S[0]对应(3,3,0)。
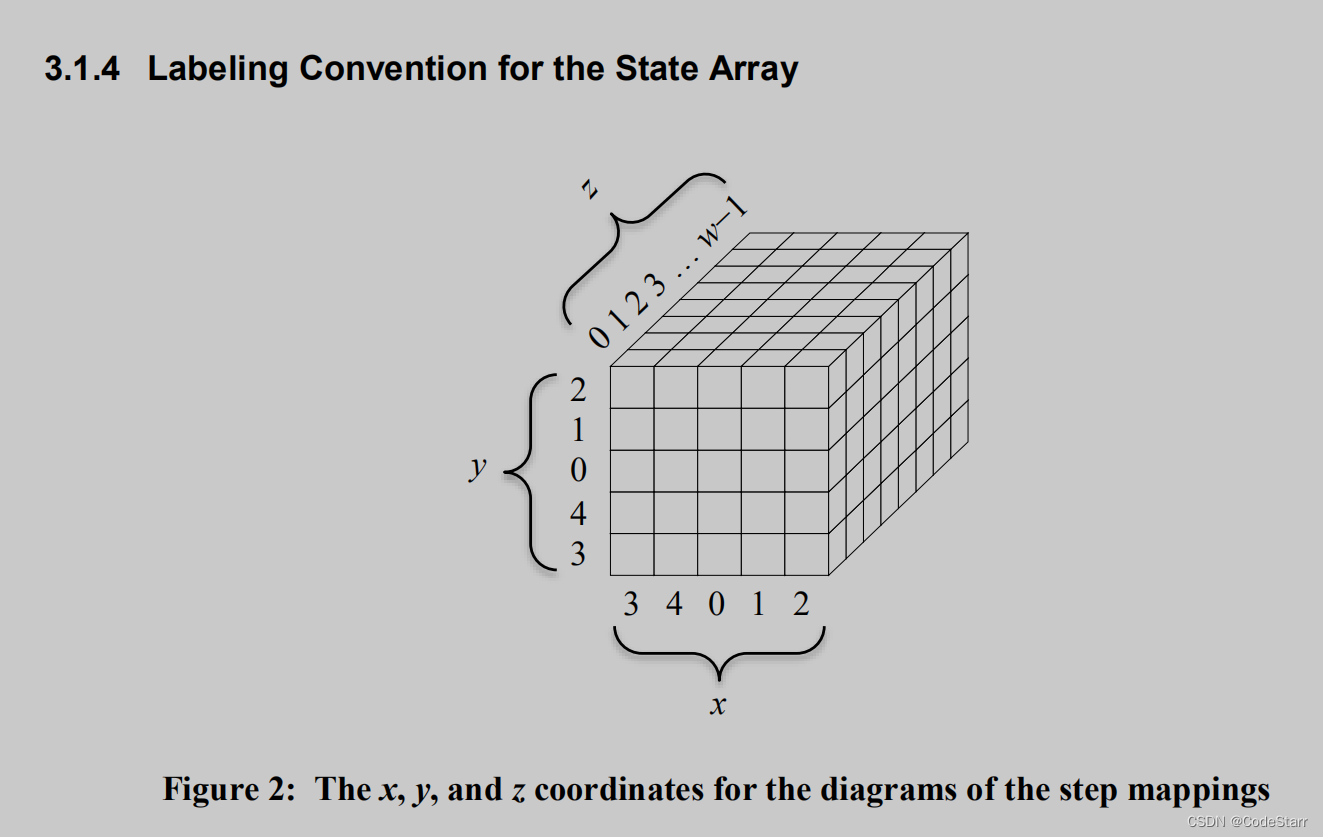
虽然中间的lane坐标为(0,0),但结合3.1.2和3.1.3,从代码的角度看,可以通过对5取余来处理,也就是说把数组第一个元素当成中间的lane即可。
3.2 Step Mappings
step mapping == Rnd == A round of a KECCAK-p permutation == round function,由5个函数组成。
构成Rnd(A round of a KECCAK-p permutation)的5个函数:
θ, ρ, π, χ, ι
or
theta, rho, pi, chi, iota
- 输入参数:state array A
- 返回:state array A’
iota额外需要一个round index参数 ir。
这一部分会比较绕,而且是以bit为单位进行讲解,但在代码中则是以ullLane(8字节unsigned long long)为单位进行运算。
theta
C[x,z]=A[x,0,z]
^ A[x,1,z]
^ A[x,2,z]
^ A[x,3,z]
^ A[x,4,z]
D[x,z]=C[(x-1) mod 5, z]
^ C[(x+1) mod 5, (z-1) mod w]
A′[x,y,z] = A[x, y, z] ^ D[x,z]
C:将5个plane面进行异或,在代码层面会得到5个ullLane(1个plane);
D:将column两两异或,在代码层面,相当于将8字节整型向高地址移位(小端整型,所以左移),得到的仍是5个ullLane;
将每个plane与plane D中异或后返回state array。
rho
这个函数的作用是将(0,0,z)以外的lane进行循环位移,offset表如下:
| x = 3 | x = 4 | x = 0 | x = 1 | x = 2 | |
|---|---|---|---|---|---|
| y = 2 | 153 | 231 | 3 | 10 | 171 |
| y = 1 | 55 | 276 | 36 | 300 | 6 |
| y = 0 | 28 | 91 | 0 | 1 | 190 |
| y = 4 | 120 | 78 | 210 | 66 | 253 |
| y = 3 | 21 | 136 | 105 | 45 | 15 |
因为(0,0,z)这个中间的lane不需要变化,所以一共移动24个lane:
x,y = (1,0)
d = {}
for t in range(24): # 23 times
d[t] = (x,y)
x,y = (y, (2*x + 3*y)%5) # 这个公式恰好遍历24个lane
print(len(d)) # 24
for t,v in d.items():
print(v)
# z = (z - (t+1)*(t+2) /2) % w
# 以下省略w
print("t=%d offset = %d\n" % (t,(-(t+1)*(t+2)/2)))
# 24
# (1, 0)
# t=0 offset = -1
# (0, 2)
# t=1 offset = -3
# (2, 1)
# t=2 offset = -6
# (1, 2)
# t=3 offset = -10
# (2, 3)
# t=4 offset = -15
# (3, 3)
# t=5 offset = -21
# (3, 0)
# t=6 offset = -28
# (0, 1)
# t=7 offset = -36
# (1, 3)
# t=8 offset = -45
# (3, 1)
# t=9 offset = -55
# (1, 4)
# t=10 offset = -66
# (4, 4)
# t=11 offset = -78
# (4, 0)
# t=12 offset = -91
# (0, 3)
# t=13 offset = -105
# (3, 4)
# t=14 offset = -120
# (4, 3)
# t=15 offset = -136
# (3, 2)
# t=16 offset = -153
# (2, 2)
# t=17 offset = -171
# (2, 0)
# t=18 offset = -190
# (0, 4)
# t=19 offset = -210
# (4, 2)
# t=20 offset = -231
# (2, 4)
# t=21 offset = -253
# (4, 1)
# t=22 offset = -276
# (1, 1)
# t=23 offset = -300
计算出来的偏移为负值,对于unsigned long long小端存储类型来说是左移,与表格中的正值都是向z轴的正方向移动。
pi
该函数的作用是将中心以外的各个lane进行重新排列(乾坤大挪移 嘿哈)。
# A'[x,y] = A[(x + 3*y) % 5, x]
x,y = (1,0)
s = set()
for t in range(24):
s.add((x,y))
print(x,y)
x,y = (x + 3*y) % 5, x # 这个公式也恰好遍历24个lane
print(len(s)) # 24
chi
该函数是对每个row进行置换:
A′[x,y,z] = A[x,y,z]
^ ( (~A[(x+1) % 5, y, z])
& A[(x+2) % 5, y, z])
当然在代码层面,还是以lane为单位进行操作的。
而且对于pi和chi两个置换函数,不要直接对原state进行操作,需要拷贝副本。
iota
这一函数的目的是使(0,0)这个lane与 round constant进行异或,因为这个lane受round index影响,而另外24个lane不会经过iota函数处理。
如前所说,iota函数需要一个round index参数,即3.3部分的Keccak_p函数的循环索引。
伪代码如下:
keccak_state iota(keccak_state A, uint32_t ir)
{
// ir = Algorithm7(b, nr) round index
keccak_state retA = A;
// uint32_t w = b / 25; // 64
// uint32_t l = log2(w); // 6
// uint64_t RC[w] = {0}; // round constant
// uint32_t j = 0;
for (j = 0; j <= l; ++j)
{
RC[2 * *j - 1] = rc(j + 7 * ir);
// the last one is RC[w-1]
}
// for all 0 <= z <= w
retA[0, 0, z] = retA[0, 0, z] ^ RC[z];
return retA;
}
可以看出,RC数组其实是固定的,并不需要在运行时计算,硬编码即可:
#define NUMBER_OF_ROUNDS 24
static const uint64_t roundconstants[NUMBER_OF_ROUNDS] = {
0x0000000000000001ULL, 0x0000000000008082ULL,
0x800000000000808aULL, 0x8000000080008000ULL,
0x000000000000808bULL, 0x0000000080000001ULL,
0x8000000080008081ULL, 0x8000000000008009ULL,
0x000000000000008aULL, 0x0000000000000088ULL,
0x0000000080008009ULL, 0x000000008000000aULL,
0x000000008000808bULL, 0x800000000000008bULL,
0x8000000000008089ULL, 0x8000000000008003ULL,
0x8000000000008002ULL, 0x8000000000000080ULL,
0x000000000000800aULL, 0x800000008000000aULL,
0x8000000080008081ULL, 0x8000000000008080ULL,
0x0000000080000001ULL, 0x8000000080008008ULL
};
对于SHA3中每个lane,长度为8字节(64 bits),其中可置为1的下标为代码中的2 * *j - 1,如下:
0x80000000 8000808B
至于生成它的函数rc(t),根据keccak原文档 1.2节,它其实是一个线性反馈移位寄存器(LFSR):
// rc[t] = (x^t mod x^8 + x^6 + x^5 + x^4 + 1) mod x in GF(2)[x].
int LFSR86540(uint8_t* LFSR)
{
int result = ((*LFSR) & 0x01) != 0;
if (((*LFSR) & 0x80) != 0)
// Primitive polynomial over GF(2): x^8+x^6+x^5+x^4+1
(*LFSR) = ((*LFSR) << 1) ^ 0x71; // 0111 0001
else
(*LFSR) <<= 1;
return result;
}
void KeccakInitializeRoundConstants()
{
uint8_t LFSRstate = 0x01;
unsigned int ir, j, bitPosition;
uint8_t nr = 24;
uint64_t KeccakRoundConstants[64] = {0};
for (ir = 0; ir < nr; ir++) {
KeccakRoundConstants[ir] = 0;
for (j = 0; j < 7; j++) {
bitPosition = (1 << j) - 1; //2^j-1
if (LFSR86540(&LFSRstate))
KeccakRoundConstants[ir] ^= (uint64_t)1 << bitPosition;
}
}
for (ir = 0; ir < 24; ++ir)
{
printf("%016llx\n", KeccakRoundConstants[ir]);
}
}
3.3 KECCAK-p[b, nr]
Rnd函数:
Rnd(A, ir) = iota(chi(pi(rho( theta(A) ))), ir)
Keccak-p[b, nr]有nr轮Rnd迭代,如下:
string Keccak_p(string s/*length b*/,int nr) // Algorithm 7
{
string s;
keccak_state A = convertS2A(s);
uint32_t w = b / 25; // 64
uint32_t l = log2(w); // 6
for(int ir = 12+2*l-nr; ir <= 12+2*l-1; ++ir)
{
A = Rnd(A, ir);
}
s = convertA2S(A);
return s;
}
在代码中,s是单字节数组,state array则是ull类型数组,所以convertS2A也是按照小端存储来转换。
沿着z轴方向,相当于从低地址到高地址。
3.4 KECCAK-f
原版本keccak中定义了KECCAK-f ,它其实是nr==12+2l时的keccak-p,也是SHA3最终选用的操作:
KECCAK-f[b] = KECCAK-p[b, 12+2*l]
SHA3选用了比特流长度b==1600,即KECCAK-p[1600, 24],相当于是KECCAK-f[1600]
4 SPONGE CONSTRUCTION
Keccak采用的算法结构叫做海绵结构。
string Z = SPONGE[f, pad, r](string N, uint d)
3 components:
- f :
- An underlying function on fixed-length strings;
- b is called the width of f;
- In SHA-3, f is invertible, although the sponge construction does not require f to be invertible.
- r:
- A parameter called the rate
- capacity,c == b - r,specified in Sec. 5.2
- pad: A padding rule
- m = len(N), (m + len(pad(r, m)) ) mod r == 0
2 inputs:
- N: a bit string
- d: bit length of the output string
Output:
- string Z of length d
海绵结构的流程(对应代码中的final函数)可看作以下几步:
- pad
- absorbing 吸入,string–>State Array,
- 轮函数执行f(),即keccak-f(),且每“吸入” 1个分组(rate 字节)就执行一次
- squeezing 挤出,State Array–>string of length d,而且每“挤出”1个分组,就要再执行一次f()。
在代码中第2、3步相当于hash udpate。
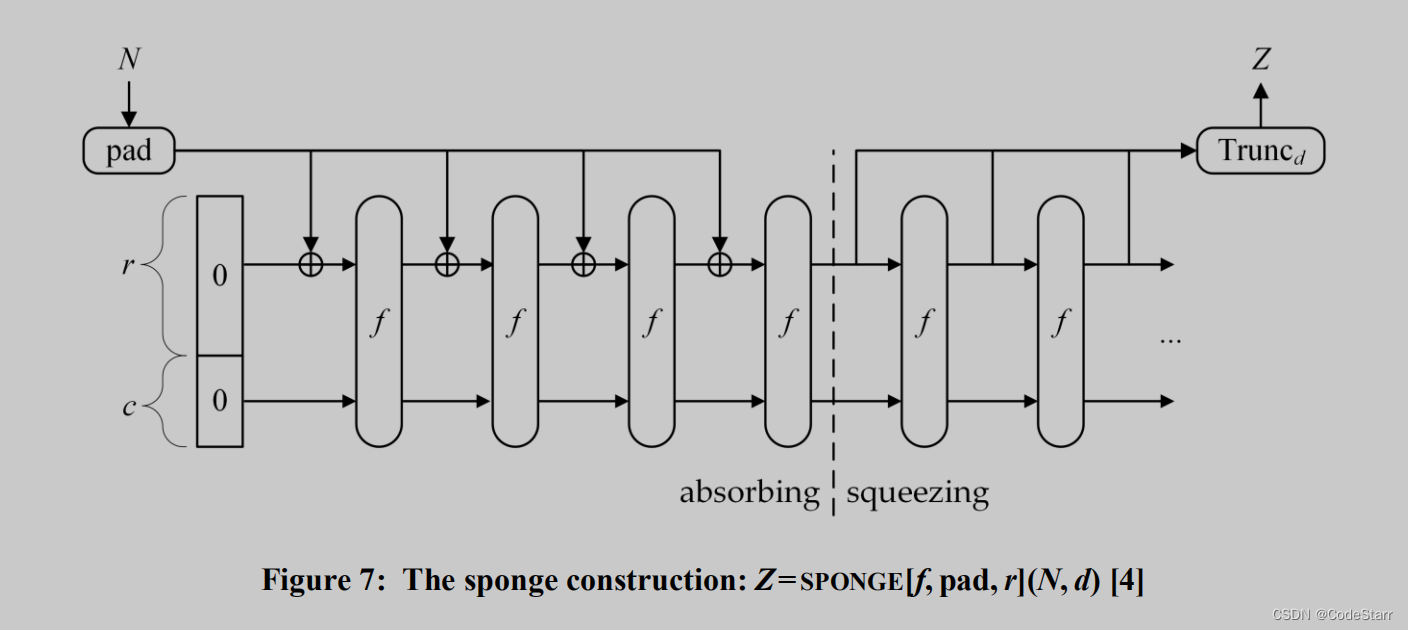
海绵结构和rate,这俩词非常形象,笔者一开始把rate理解为valid buffer,因为这些数据其实是存储在block中的,只不过不像sha2那样把block缓冲区填满。函数f相当于挤压海绵,吸收数据和输出摘要,都需要“挤压”一下。
根据第7章,SHA-3 hash分组大小rate如下表:
| Hash | SHA3-224 | SHA3-256 | SHA3-384 | SHA3-512 |
|---|---|---|---|---|
| BlockSize(bytes) | 144 | 136 | 104 | 72 |
5.1 Specification of pad10*1
The padding rule for KECCAK is called multi-rate padding.
inputs:
- r : rate
- m : len(N)
output:
- string P, (m + len(pad(r, m)) ) mod r == 0,即填充完后,数据长度是r的倍数,所以r就是分组大小。
uint pad10x1(uint r, uint m)
{
uint P;
uint j = (-m-2) % r;
// (m + len(P)) % r == 0
// len(P) == (-m) % r
P = (1<<j) + 1; // 1 || 0*j || 1
return P;
}
实际的补充方法,请参见附录B。
5.2 Specification of KECCAK[c]
根据第4节海绵结构,总结一下keccak的组成:
- 海绵函数Keccak-p[b, 12+2l]
- 填充规则pad10*1
- rate(<b),其实就是分组大小
如3.1所述,比特流长度b有7个可选值。当选用最大值b==1600时,就只有rate不确定了。而rate就由c(capacity)决定了:
KECCAK[c](N, d) = SPONGE[
f = KECCAK-p[1600, 24]
,pad = pad10*1
,r = 1600–c](N, d)
6 SHA-3 FUNCTION SPECIFICATIONS
6.1 SHA-3 Hash Functions
SHA3有4个基于KECCAK[c] 定义的hash函数:
SHA3-224(M) = KECCAK[448] (M || 01, 224)
SHA3-256(M) = KECCAK[512](M || 01, 256)
SHA3-384(M) = KECCAK[768] (M || 01, 384)
SHA3-512(M) = KECCAK[1024](M || 01, 512)
如第1部分所述,消息后面会追加2 bits,用来区分hash函数和XOFs。
所以SHA3的这4个hash算法,相当于给消息追加01后的Keccak-f[1600]。
另外可以观察到,c==2d,也就是说,capacity是输出摘要长度的两倍。
6.2 SHA-3 Extendable-Output Functions
SHA3的两个XOF,SHAKE128 和 SHAKE256,也是基于KECCAK[c] 定义的:
SHAKE128(M, d) = KECCAK[256] (M || 1111, d)
SHAKE256(M, d) = KECCAK[512] (M || 1111, d)
6.3 Alternate Definitions of SHA-3 Extendable-Output Functions
还有两个原版sponge functions, RawSHAKE128 和 RawSHAKE256:
RawSHAKE128(J, d) = KECCAK[256] (J || 11, d)
RawSHAKE256(J, d) = KECCAK[512] (J || 11, d)
这个11后缀用以区分RawSHAKE和SHA3 SHAKE
当J = M || 11时,就等价于SHAKE128和SHAKE256。这个11后缀,则是用来兼容RawSHAKE和Sakura coding scheme。
A Security
A.1 Summary
| Function | Output Size | Collision | Preimage | 2nd Preimage |
|---|---|---|---|---|
| SHA3-224 | 224 | 112 | 224 | 224 |
| SHA3-256 | 256 | 128 | 256 | 256 |
| SHA3-384 | 384 | 192 | 384 | 384 |
| SHA3-512 | 512 | 256 | 512 | 512 |
| SHAKE128 | d | min(d/2, 128) | ≥ min(d, 128) | min(d, 128) |
| SHAKE256 | d | min(d/2, 256) | ≥ min(d, 256) | min(d, 256) |
其中,Collision,Preimage,2nd Preimage为抵抗攻击的安全级别。
B Examples
B.1 Conversion Functions
这里给出了二进制和十六进制的转换法。简单地说,在每个字节中bit是小端存储。
以0xA32E为例:
# support trunc
def h2b(h:int, n:int):
ret = ""
b = bin(h)[2:]
print(b) # 10100011 00101110
nBy = len(b) // 8
for i in range(nBy):
ret += b[8*i:8*i+8][-1::-1]
ret += " "
return ret[:n];
# 0xA32E为大端存储 "\xA3\x2E"
print(h2b(0xA32E, 14))
# 11000101 01110
B.2 Hexadecimal Form of Padding Bits
以上运算是以bit为单位的,但在实际应用中,数据N以及rate肯定是以字节为单位,也就是说r和m均为8的倍数。
在原文档附录B中,给出了以下公式,q为需要填补的字节数:
// m单位: byte
q = (r/8) - (m % (r/8))
这个很好理解,就是补充字节满足整体长度为rate的倍数,等价于下面这个公式:
# 单位: byte
8q == r - 8m % r
5.1 填充方法部分是以bit为单位讲解的,而在代码中,则是以字节为单位,更准确地说是十六进制。
结合5.1和6.1,要添加的bit流如下:
01 1 0j 1
也就是说,要填充的0的个数j,可能是4+8*n。填充结束后,还要将每个字节的bit顺序反转,如下:
def pad(j:int):
strRet = "0x"
padding = "01"
padding += "1" + "0" * j + "1"
nBy = len(padding) // 8
for i in range(nBy):
tmp = padding[8*i: 8*i+8][::-1]
strRet += "%02x" % (int(tmp, 2))
return strRet
print(pad(4))
# 0x86 q == 1
print(pad(12))
# 0x0680 q == 2
print(pad(20))
# 0x060080 q == 3
print(pad(28))
# 0x06000080 q == 4
而对于XOF,则是这样填充:
# 1111 1 0j 1
def pad_xof(j:int):
strRet = "0x"
padding = "1111"
padding += "1" + "0" * j + "1"
nBy = len(padding) // 8
for i in range(nBy):
tmp = padding[8*i: 8*i+8][::-1]
strRet += "%02x" % (int(tmp, 2))
return strRet
print(pad(2))
# 0x9f q == 1
print(pad(10))
# 0x1f80 q == 2
print(pad(18))
# 0x1f0080 q == 3
print(pad(26))
# 0x1f000080 q == 4
实现
https://github.com/C0deStarr/CryptoImp/tree/main/Hash/sha/:
- sha3.h
- sha3.c
参考资料
-
原文档 https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.202.pdf
-
https://csrc.nist.gov/publications/detail/fips/202/final
-
Keccak Team
-
原版Keccak:http://keccak.noekeon.org/Keccak-reference-3.0.pdf
-
http://keccak.noekeon.org/Sakura.pdf
-
海绵结构:http://sponge.noekeon.org/CSF-0.1.pdf