一、快速排序——时间复杂度: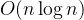 、 最坏的情况
、 最坏的情况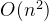
1、原理:
快速排序是通过多次比较和交换来实现排序,首先,先从数列中,任意选择一个数作为基准(或叫分界值),比如,第一个数,然后将数列中比基准小的数都放到基准左边,比基准大的数都放到基准右边,这样一趟下来之后呢,这个数列就被基准分成了左右两个独立的部分,(也就是说,此时,基准就处于数列的中间位置)。然后像刚才一样,分别继续递归这两部分,最终使得数列变得有序。
具体步骤:
1、首先,先从数列中,任意选择一个数作为基准,(比如,第一个数),通过这个基准将数据分成左右两个部分。
2、将数列中比基准小的数都放到基准左边,比基准大或者等于的数放到基准右边,这样就完成了第一趟排序,此时,基准就处于数列的中间位置,左边的数都小于这个基准,而右边的数,都大于或等于基准。
3、然后,再把左右两边像刚才一样,再分别找个基准再进行划分为两个部分,(也就是递归),直到左右两边都只有一个数时为止,此时列表已排好序。
总的来说就是,先任意取一个元素,比如a ,使得a归位,所谓归位就是说,列表被这个元素a 分成了两部分,左边都是比a小,右边都是比a大,然后再对左右两边递归完成排序。
2、举例:第一趟排序效果图:



注意:
1、如果是【left指向坑,看right,左移,找小】,用right所指的数,与基准进行比较,如果这个数>=基准,那right-1,把它向左移动一个位置,继续与基准进行比较,直到找到比基准小的这个数,然后放到left所指的坑里。——填坑
2、如果是【right指向坑,看left,右移,找大】,如果left所指的数小于等于基准,那就把left+1,把它向右移动一个位置,继续与基准进行比较,直到找到比基准大的数,然后把它放到right所指的坑里。
3、快速排序代码
def partition(li, left, right): # partition:分区
tmp = li[left]
while left < right: # 只要left和right没有重合(或叫碰头),说明还有数据没有跟基准进行比较
while left < right and li[right] >= tmp: # 坑指向left,看right,找大
right -= 1 # 只要这个数大于tmp,那right就往左移一步,继续找
li[left] = li[right] # 把右边的值写到左边空位上
while left < right and li[left] <= tmp: # 坑指向right,看left,找大
left += 1
li[right] = li[left]
li[left] = tmp # 或写li[right] = tmp,都一样,因为跳出循环时候,left=right
return left # 返回mid的值,也可以写return right
def quick_sort(li, left, right):
if left < right: # 至少有两个元素的时候,才递归
mid = partition(li, left, right) # mid出来以后说明第一个元素已经归位了,或者叫已完成第一趟排序,然后开始递归左右两部分
quick_sort(li, left, mid - 1) # 递归左边
quick_sort(li, mid + 1, right) # 递归右边
l1 = [5, 1, 6, 7, 2, 4, 8, 5]
print(l1)
quick_sort(l1, 0, len(l1) - 1)
print(l1)
# 结果:
[5, 1, 6, 7, 2, 4, 8, 5]
[1, 2, 4, 5, 5, 6, 7, 8]
4、查看每趟归并后的结果
如果想看每趟归并后的结果怎么办?定义一个全局变量,用来记录趟数,代码如下:
i = 0 # 定义i用来计数
def partition(li, left, right):
global i # !!!!
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp: # 填left所指的坑
right -= 1
li[left] = li[right]
# print(li, "right") # 每一次填left坑的结果
while left < right and li[left] <= tmp: # 填right所指的坑
left += 1
li[right] = li[left]
# print(li, "left") # 每一次填right坑的结果
i += 1 # !!!!
li[left] = tmp # 或写li[right] = tmp,因为跳出循环时候,left=right
print("第%s趟归位后的结果:" % i, li) # 每一趟归并后的结果 # !!!!
return left # 或写成return left
def quick_sort(li, left, right):
if left < right:
mid = partition(li, left, right) # mid出来以后说明第一个元素已经归位了,或者叫已完成第一趟排序
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
l1 = [5, 1, 6, 7, 2, 4, 8, 5]
quick_sort(l1, 0, len(l1) - 1)
print(l1)
# 结果:
第1趟归位后的结果: [4, 1, 2, 5, 7, 6, 8, 5]
第2趟归位后的结果: [2, 1, 4, 5, 7, 6, 8, 5]
第3趟归位后的结果: [1, 2, 4, 5, 7, 6, 8, 5]
第4趟归位后的结果: [1, 2, 4, 5, 5, 6, 7, 8]
第5趟归位后的结果: [1, 2, 4, 5, 5, 6, 7, 8]
[1, 2, 4, 5, 5, 6, 7, 8]5、快速排序所存在的问题
1、快速排序最坏情况
比如,当列表是个降序时,此时再用快速排序,每次都只排了一个数,或者说,每次递归都只递归了一边,不会像平时那样左右两边都会递归,一趟能排好多数,所以这里最坏的情况就是,不是
,总的快速排序复杂度就是
,当然,这种最坏的情况是比较少的。
例如:当li=[9,8,7,6,5,4,3,2,1]时候


具体代码:
i = 0 # !!
def partition(li, left, right):
global i # !!!!
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp: # 填left所指的坑
right -= 1
li[left] = li[right]
# print(li, "right") # 每一次填left坑的结果
while left < right and li[left] <= tmp: # 填right所指的坑
left += 1
li[right] = li[left]
# print(li, "left") # 每一次填right坑的结果
i += 1 # !!!!
li[left] = tmp # 或写li[right] = tmp,因为跳出循环时候,left=right
print("第%s趟归位后的结果:" % i, li) # 每一趟归并后的结果 # !!!!
return left # 或写成return left
def quick_sort(li, left, right):
if left < right:
mid = partition(li, left, right) # mid出来以后说明第一个元素已经归位了,或者叫已完成第一趟排序
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
l1 = [9, 8, 7, 6, 5, 4, 3, 2, 1] # 快排最坏情况
quick_sort(l1, 0, len(l1) - 1)
print(l1)
# 结果:
第1趟归位后的结果: [1, 8, 7, 6, 5, 4, 3, 2, 9]
第2趟归位后的结果: [1, 8, 7, 6, 5, 4, 3, 2, 9]
第3趟归位后的结果: [1, 2, 7, 6, 5, 4, 3, 8, 9]
第4趟归位后的结果: [1, 2, 7, 6, 5, 4, 3, 8, 9]
第5趟归位后的结果: [1, 2, 3, 6, 5, 4, 7, 8, 9]
第6趟归位后的结果: [1, 2, 3, 6, 5, 4, 7, 8, 9]
第7趟归位后的结果: [1, 2, 3, 4, 5, 6, 7, 8, 9]
第8趟归位后的结果: [1, 2, 3, 4, 5, 6, 7, 8, 9]
[1, 2, 3, 4, 5, 6, 7, 8, 9]2、最大深度问题
对于递归来说,不仅会消耗一部分系统资源,还会遇到最大深度问题。
例如:利用range( )函数,创建一个长度为1000倒叙的列表,此时就会递归1000次,就会报错,遇到最大深度问题。
l1 = list(range(1000, 0, -1)) # 创建一个长度为1000倒叙的列表
quick_sort(l1, 0, len(l1) - 1)
print(l1)
# 结果:
RecursionError: maximum recursion depth exceeded in comparison
进程已结束,退出代码 1怎么解决?
修改最大深度。在代码最上面写上下面两行。
import sys
sys.setrecursionlimit(10000) # 设置最大递归深度为10000修改后的完整代码:
import sys
sys.setrecursionlimit(10000) # 设置最大递归深度
def partition(li, left, right):
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp:
right -= 1
li[left] = li[right]
while left < right and li[left] <= tmp:
left += 1
li[right] = li[left]
li[left] = tmp
return left
def quick_sort(li, left, right):
if left < right: # 至少有两个元素的时候,才递归
mid = partition(li, left, right)
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
l1 = list(range(1000, 0, -1)) # 创建一个长度为1000倒叙的列表
quick_sort(l1, 0, len(l1) - 1)
print(l1)
# 结果:
[1, 2, 3, 4, 5, 6, ......一直到999,1000]6、怎么避免出现最坏情况?
解决办法:利用随机化版本的快速排序方法。但这种方法也并不能完全避免出现最坏情况,因为,随机数也有可能找到最两端的数。但一般情况下,出现最坏概率比较下,通常快排没啥大的问题。
之前我们基准取的都是列表里的第一个元素,现在我们不取第一个元素了,而是从列表里随机取一个元素,让它作为基准。
具体做法:
1、导入random模块,利用:random.choice( 列表名),从列表里随机取一个数。
2、让这个数跟列表的第一个数,交换一下。
列表的第一个数:li[0]
从列表里随机取个数:a = random.choice(列表名),
找到它在列表中的位置a_loc = li.index(a)
将随机数与列表第一个数进行交换,使得随机数作为基准
li[0], li[a_loc] = a, li[0]
3、再按照之前写的归位方法(partition函数),把第一个拿出来,进行比较后归位再对两边递归等等,后面操作跟之前都是一样的了。
延申:从列表里随机取一个数的方法。
import random
l1 = [1, 4, 5, 2]
print(random.choice(l1))
# 结果
1 或2 或4 或5举例:避免最坏情况发生的例题。
例如:创建一个长度为5倒叙的列表。
import random
i = 0
def partition(li, left, right):
global i # !!!!
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp:
right -= 1
li[left] = li[right]
while left < right and li[left] <= tmp:
left += 1
li[right] = li[left]
i += 1 # !!!!
li[left] = tmp
print("第%s趟归位后的结果:" % i, li) # 每一趟归并后的结果 # !!!!
return left
def quick_sort(li, left, right):
if left < right:
mid = partition(li, left, right)
quick_sort(li, left, mid - 1)
quick_sort(li, mid + 1, right)
l1 = list(range(5, 0, -1)) # 创建一个长度为5倒叙的列表
print(l1)
a = random.choice(l1)
print("列表随机取的数是:%d ,列表第一个元素是:%d" % (a, l1[0]))
a_loc = l1.index(a) # 找到随机数在列表里的位置
l1[0], l1[a_loc] = a, l1[0] # 将随机数与列表第一个数进行交换,使得随机数作为基准
print("互换后的列表:", l1)
quick_sort(l1, 0, len(l1) - 1)
print(l1)
# 结果:
[5, 4, 3, 2, 1]
列表随机取的数是:3 ,列表第一个元素是:5
互换后的列表: [3, 4, 5, 2, 1]
第1趟归位后的结果: [1, 2, 3, 5, 4]
第2趟归位后的结果: [1, 2, 3, 5, 4]
第3趟归位后的结果: [1, 2, 3, 4, 5]
[1, 2, 3, 4, 5]
进程已结束,退出代码 0