前言:前面我们学习了顺序表、单链表、栈、队列，今天我们就开始新的学习吧，今天我们将进入堆的学习！(最近博主处于低谷期)一起加油吧各位。

💖 博主CSDN主页:卫卫卫的个人主页 💞
👉 专栏分类:数据结构 👈
💯代码仓库:卫卫周大胖的学习日记💫
💪关注博主和博主一起学习!一起努力！

---

学前必读:

1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是 ，则它就是满二叉树。
2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。(至于二叉树，博主会在下一篇博客中给大家讲解，各位友友不用心急)

---

什么是堆

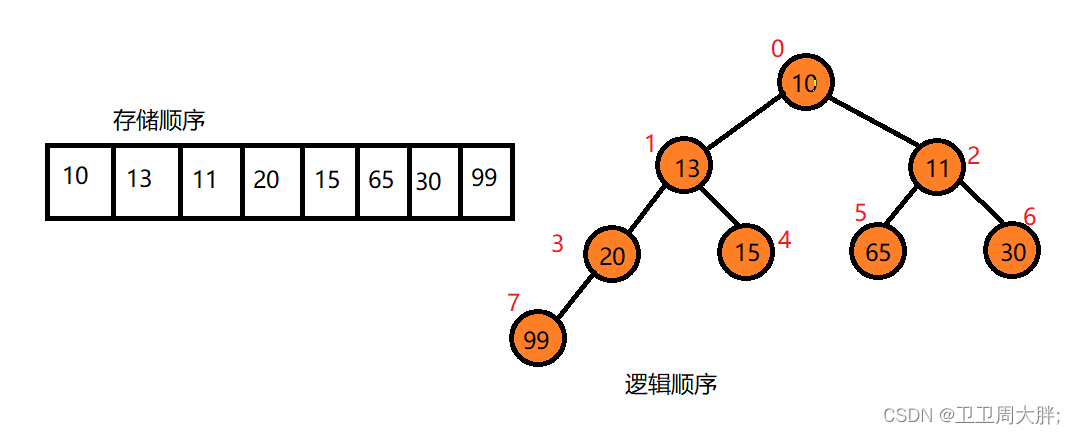
堆(Heap):我们可以通俗的理解成一种二叉树，但最大值或最小值是存在上面的，且堆中某个节点的值总是不大于或不小于其父节点的值。并且堆总是一棵完全二叉树。光看文字我们可能无法很清晰的理解堆，我们来看下图。

---

堆的基本功能

1. 插入数据
2. 取堆顶的数据
3. 删除根节点(最顶部)的数据
4. 堆的数据个数
5. 堆的判空

---

堆的功能实现

思路导读:要想实现堆，我们首先得定义一个结构体，里面存放一个指针，和一个size记录堆中数据个数，一个capacity记录空间的容量看是否需要扩容。如果有不懂的友友可以去看我前面的文章。
代码实现：

typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

---

堆的初始化

思路导读:堆的初始化还是一样的，我们把指针置为空，元素个数清零，空间容量清零即可。
代码实现：

void HeapInit(HP* php)//堆的初始化
{
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

---

堆的销毁

思路导读:堆的销毁方法也不变，只需要将该指针开辟的空间释放掉，然后将指针置为空，元素个数清零，空间容量清零即可。
代码实现：

typedef int HPDataType;//定义一个变量

void HeapDestory(HP* php)//堆的销毁
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

---

堆的插入数据

思路导读:首先我们在插入的数据应该考虑，(假设我们建的堆是小堆)是直接插入在堆的头部还是在尾部，首先我们来看看头部是不是可行的，如果我们插入在头部，当插入的这个数是小于头部这个数的时候，那么我们就需要调整整个堆中的数据，来一一判断，可想而知这种方式是多么的麻烦，并且时间复杂度也相对来说较高。那么我们考虑把这个数据放在堆的尾部的时候看看是什么情况，我们将堆的数据放在尾部如果比它的父亲结点还小那么我们就交换它和父亲结点的位置即可。我们可以通过下图来对比分析。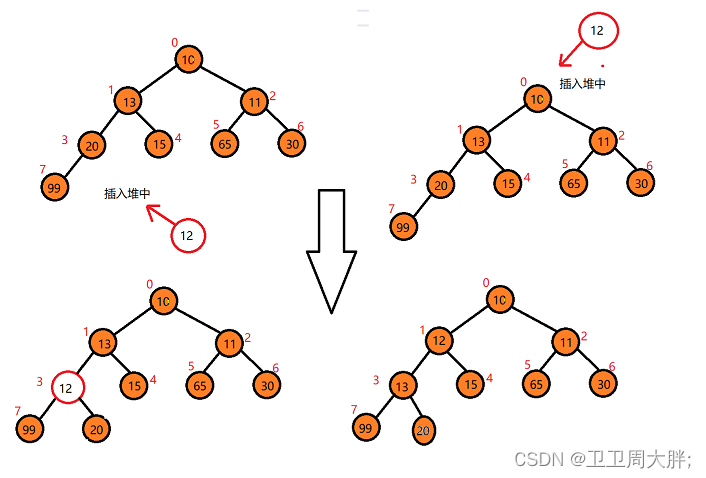
尾部插入代码实现:当然这个还是比较简单的，不懂的可以看前面的文章

void HeapPush(HP* php, HPDataType x)//插入数据
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;//先存放在尾部
}

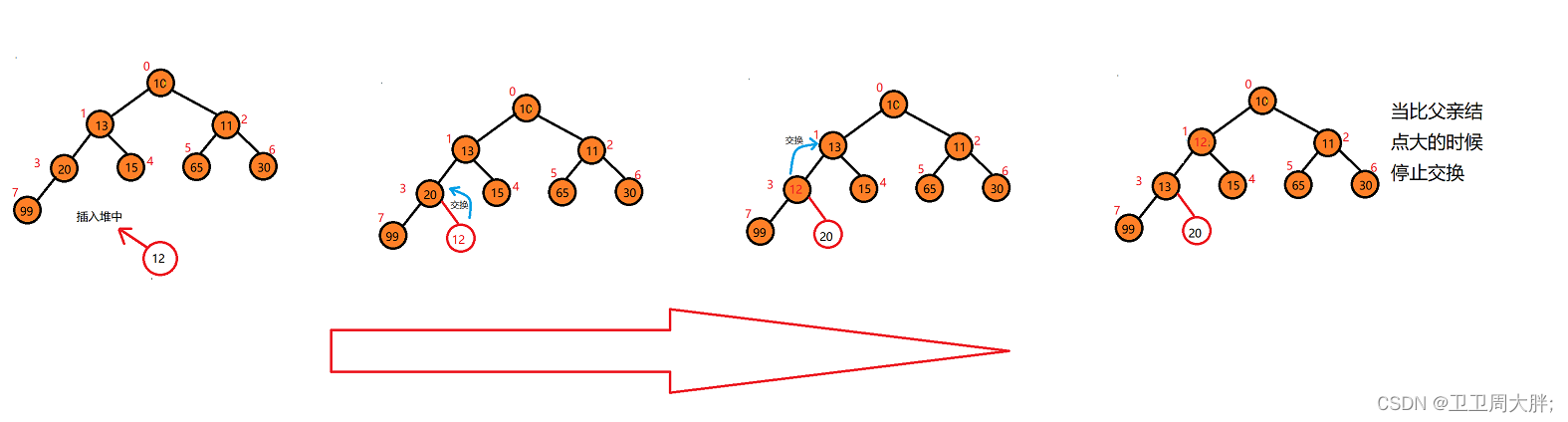
我们通过图可知道，我们将数据放在尾部插入，然后将数据和它的父亲结点比较，如果比它的父亲结点还要小，我们就将它们俩俩交换，如果一直没有找到那么什么时候停止呢？就是当走到下标为0的时候停止(如下图)。因此我们要写一个函数将插入的数据向上调整，来保证我们的堆在插入后仍然成立。

代码实现:

void AdjustUp(HPDataType* a, int child)//向上调整
{
	assert(a);
	int parent = (child - 1) / 2;//父亲节点的下标
	while (child > 0)
	{
		if (a[child] < a[parent])//当孩子节点比父亲还小
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

整体插入代码实现:

void Swap(int* x, int* y)//交换
{
	int tmp = 0;
	tmp = *x;
	*x = *y;
	*y = tmp;
}

void AdjustUp(HPDataType* a, int child)//向上调整
{
	assert(a);
	int parent = (child - 1) / 2;//父亲节点的下标
	while (child > 0)
	{
		if (a[child] < a[parent])//当孩子节点比父亲还小
		{
			Swap(&a[child], &a[parent]);//两两交换
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)//插入数据
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;//先存放在尾部
 	AdjustUp(php->a,php->size);
	php->size++;
}

---

取堆顶的数据

思路导读:因为我们堆顶的数据在数组中存储的时候就放在了数组的头部，因此我们只需要返回数组下标为0的那个数即可。
代码实现：

HPDataType HeapTop(HP* php)// 取堆顶的数据
{
	assert(php);
	return php->a[0];
}

删除根节点(堆顶)的数据

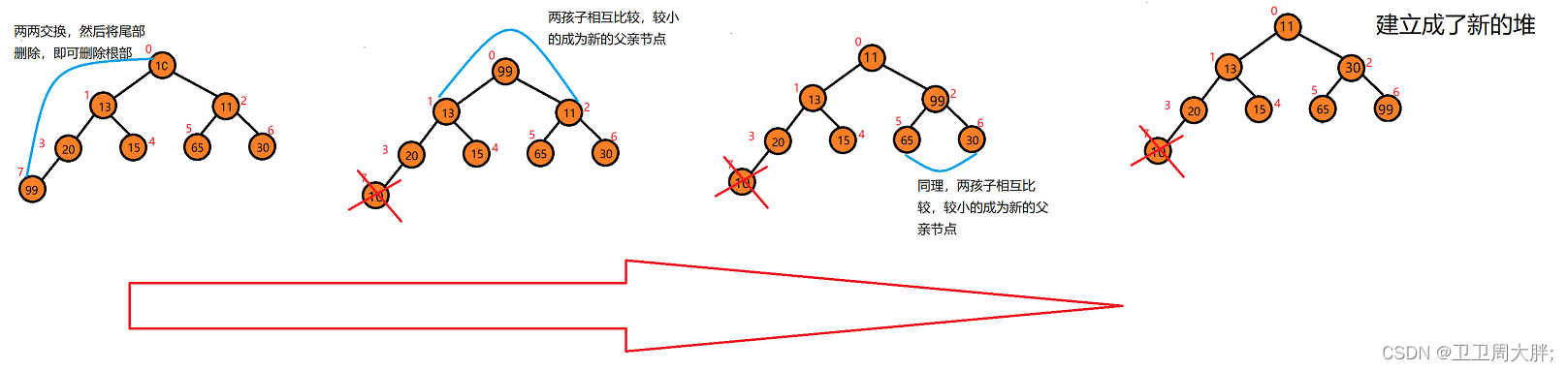
思路导读:1.如何删除根节点我们删除根节点我们首先想到的就是直接删除头部的节点，我们来试想一下直接删除根节点，如果直接删除头部节点，那么我们整个堆的数据都要立刻开始动（即数据都往前诺一位）在不考虑删除堆后是否还是堆，因此直接删除根节点是十分麻烦的。我们换一个思路，我们将根节点，和尾部节点的数据交换位置，然后直接尾删数据，那么我们整个堆在不考虑交换后是否仍然是堆的情况下，即可很快速的完成删除根节点。
2. 向下调整我们在完成删除根部节点之后，我们尾部的数据放在了根部，我们自然而然的就要考虑这个树是否仍然是一个堆了，因此我们要把交换后的这个数与它的孩子节点比较，如果比它们大即交换数据，一直到比它们小为止，或者走到树的尾部。如下图所示

代码实现：

void AdjustDown(HPDataType* a, int size, int parent)//向下调整
{
	assert(a);
	int child = parent * 2 + 1;//找到第一个孩子
	while (child < size)
	{
		//看俩个孩子谁更小，交小的那个与父亲去比较
		if (a[child] > a[child + 1] && (child+1) < size)
		{
			child += 1;
		}
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
			parent = child;//让父亲和儿子往下走
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(HP* php)//删除根节点(最顶部)的数据
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[php->size - 1], &php->a[0]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

堆的数据个数

思路导读:我们在前面记录了一个size负责记录数据的个数，因此我们只需要直接返回size即可。
代码实现:

size_t HeapSize(HP* php) //堆的数据个数
{
	assert(php);
	return php->size;
}

---

堆的判空

思路导读:我们只需要判断size中的数据是否为0即可。
代码实现:

bool HeapEmpty(HP* php) //堆的判空
{
	assert(php);
	return php->size == 0;

}

---

整体函数测试

void Test1()
{
	int array[] = { 27,15,19,18,28,34,65,49,25,37 };
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i < sizeof(array) / sizeof(int); i++)
	{
		HeapPush(&hp, array[i]);//插入数据
	}
	int k = HeapSize(&hp);
	while (k--)
	{
		printf("%d ",HeapTop(&hp));//获取堆顶数据
		HeapPop(&hp);
	}
	//Print(&hp);
	HeapDestory(&hp);

}

int main()
{
	Test1();
}

运行结果:
自己手动排一下，看看是否建堆成功。

---

结语：今天的内容就到这里吧，谢谢各位的观看，如果有讲的不好的地方也请各位多多指出，作者每一条评论都会读的，谢谢各位。

---

🫵🫵🫵 祝各位接下来好运连连 💞