1、概述
动力学以牛顿第二定律为核心，这个定律指出了力、加速度、质量三者间的关系。
质点动力学有两类基本问题：
一是已知作用于质点上的力，求质点的运动，这个就是正动力学。
二是已知质点的运动，求作用于质点上的力，这个属于逆动力学。
求解第一类问题时只要对质点的运动方程取二阶导数，得到质点的加速度，代入牛顿第二定律即可求得力
求解第二类问题时需要求解质点运动微分方程或求积分。所谓质点运动微分方程就是把运动第二定律写为包含质点的坐标对时间的导数的方程。
这节主要是通过Matlab来熟悉动力学在机器人领域的实际应用。
2、动力学参数
以p560机械臂为例，我们来查看下它的动力学参数
首先还是运行机器人工具包，如果没有安装这个包的可以查阅：MATLAB的rvctools工具箱熟悉运动学【机械臂机器人示例】
接下来我们将机器人加载进来，有很多自带的机器人，这里我们选择使用p560机器人，看下这个机器人有哪些动力学相关的属性参数，通过 dyn 函数我们可以得到以下各个关节的惯性属性：
startup_rvc
mdl_puma560
p560.dyn
Link 1::Revolute(std): theta=q, d=0, a=0, alpha=1.5708, offset=0
m = 0
r = 0 0 0
I = | 0 0 0 |
| 0 0.35 0 |
| 0 0 0 |
Jm = 0.0002
Bm = 0.00148
Tc = 0.395 (+) -0.435 (-)
G = -62.61
qlim = -2.792527 to 2.792527
Link 2::Revolute(std): theta=q, d=0, a=0.4318, alpha=0, offset=0
m = 17.4
r = -0.3638 0.006 0.2275
I = | 0.13 0 0 |
| 0 0.524 0 |
| 0 0 0.539 |
Jm = 0.0002
Bm = 0.000817
Tc = 0.126 (+) -0.071 (-)
G = 107.8
qlim = -0.785398 to 3.926991
Link 3::Revolute(std): theta=q, d=0.15005, a=0.0203, alpha=-1.5708, offset=0
m = 4.8
r = -0.0203 -0.0141 0.07
I = | 0.066 0 0 |
| 0 0.086 0 |
| 0 0 0.0125 |
Jm = 0.0002
Bm = 0.00138
Tc = 0.132 (+) -0.105 (-)
G = -53.71
qlim = -3.926991 to 0.785398
Link 4::Revolute(std): theta=q, d=0.4318, a=0, alpha=1.5708, offset=0
m = 0.82
r = 0 0.019 0
I = | 0.0018 0 0 |
| 0 0.0013 0 |
| 0 0 0.0018 |
Jm = 3.3e-05
Bm = 7.12e-05
Tc = 0.0112 (+) -0.0169 (-)
G = 76.04
qlim = -1.919862 to 2.967060
Link 5::Revolute(std): theta=q, d=0, a=0, alpha=-1.5708, offset=0
m = 0.34
r = 0 0 0
I = | 0.0003 0 0 |
| 0 0.0004 0 |
| 0 0 0.0003 |
Jm = 3.3e-05
Bm = 8.26e-05
Tc = 0.00926 (+) -0.0145 (-)
G = 71.92
qlim = -1.745329 to 1.745329
Link 6::Revolute(std): theta=q, d=0, a=0, alpha=0, offset=0
m = 0.09
r = 0 0 0.032
I = | 0.00015 0 0 |
| 0 0.00015 0 |
| 0 0 4e-05 |
Jm = 3.3e-05
Bm = 3.67e-05
Tc = 0.00396 (+) -0.0105 (-)
G = 76.69
qlim = -4.642576 to 4.642576这里将6个关节的参数属性都给显示出来了，我们也可以查看单个关节的参数，比如第二个关节：p560.dyn(2)或者p560.links(2).dyn，这些属性分别说明如下：
m：关节的质量
r：关节齿轮向量，或叫质心
I：3x3的对称惯性矩阵(对称矩阵是其转置是它本身)。惯性矩阵是刚体在不同坐标轴上的转动惯量，通过对称矩阵的特征值和特征向量，可以得到刚体的主轴和转动惯量。
Jm：电机惯性
Bm：粘性摩擦力
Tc：库仑摩擦力（当然如果说忽略库仑摩擦力的情况：p560.nofriction().dyn，这样Tc都为0，没有库仑摩擦力了）
G：齿轮传动比（主动轮转速/从动轮转速 或者 从动轮齿数/主动轮齿数）比值小于1，是增速；大于1，是减速。打个比方，变速自行车，爬坡的时候，就是小齿轮带大齿轮，属于减速，这样踩起来就比较省力，轻松，但是需要多踩很多圈，需要注意的是，省力，但是不会省功。
qlim：关节转动的最大范围
获取这些属性的方法如下：
p560.links(2).m
17.4000
p560.links(1).G
-62.6111
%其他类似...3、正动力学Forward dynamics
正动力学也叫前向动力学，根据受力情况，求出角速度、角加速度的过程。
模拟Puma 560在零角度静止状态下的运动，关节力矩为零，通过 fdyn(TMAX,FTFUN) 函数，会对机器人在0~TMAX的时间内的动力学进行积分，这样可以获取到时间T,关节位置q,关节速度qd
p560=p560.nofriction( );
tic
[T,q,qd]=p560.fdyn(10,[],qz);
toc
%时间已过 1.366665 秒。也可以自行设置力矩来获取位置与速度：
torqfun = [1 2 3 4 5 6];
[T,q,qd]=p560.fdyn(10,[],torqfun);由此产生的运动，我们将其角速度随着时间绘制出来：
set(gcf,'Position',[10,10, 800, 1000]);
subplot(6,1,1); plot(T,qd(:,1)); xlabel('Time (s)'); ylabel('Joint 1 (rad)')
subplot(6,1,2); plot(T,qd(:,2)); xlabel('Time (s)'); ylabel('Joint 2 (rad)')
subplot(6,1,3); plot(T,qd(:,3)); xlabel('Time (s)'); ylabel('Joint 3 (rad)')
subplot(6,1,4); plot(T,qd(:,4)); xlabel('Time (s)'); ylabel('Joint 4 (rad)')
subplot(6,1,5); plot(T,qd(:,5)); xlabel('Time (s)'); ylabel('Joint 5 (rad)')
subplot(6,1,6); plot(T,qd(:,6)); xlabel('Time (s)'); ylabel('Joint 6 (rad)')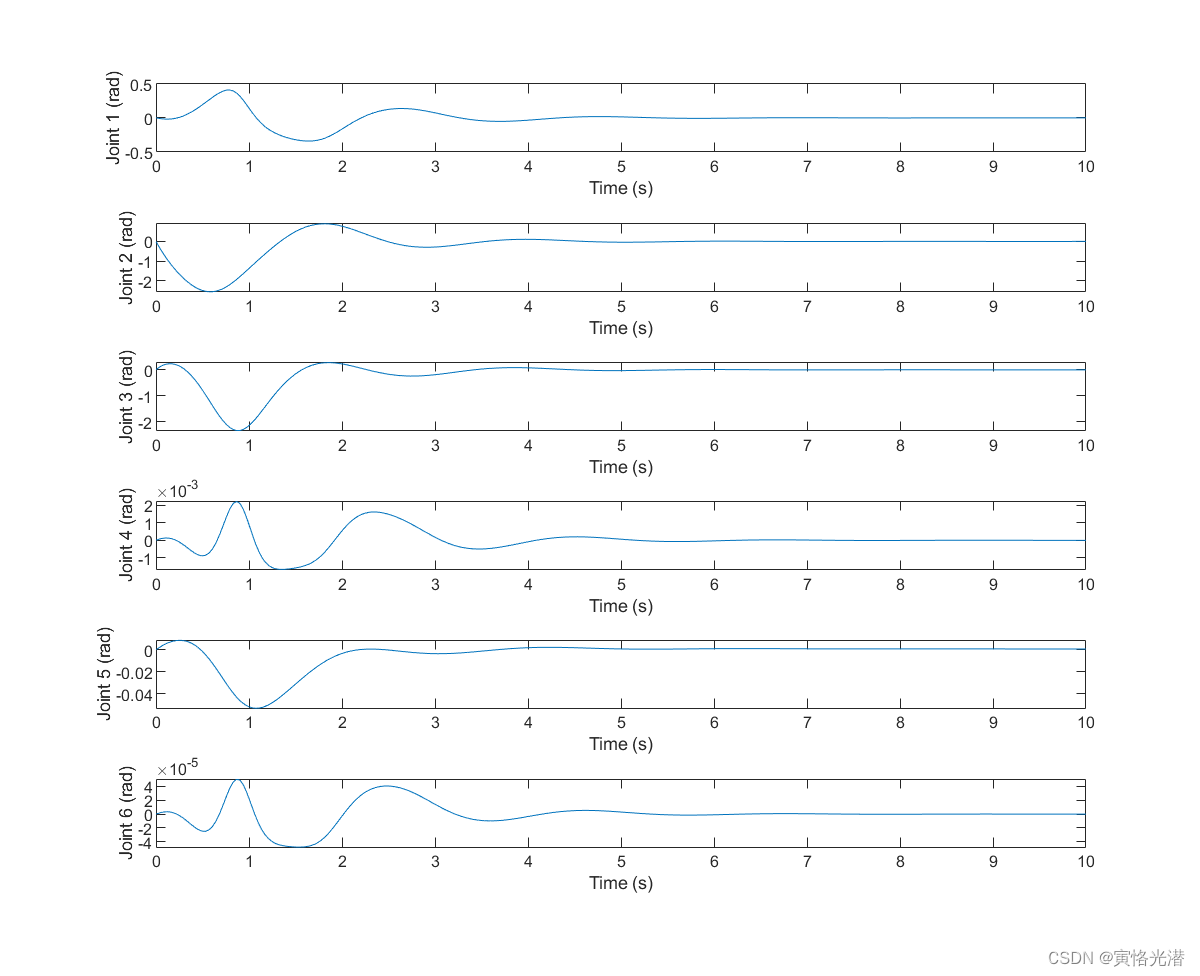
或者这样画图，更直观，我这里就选1~4个关节的速度：
figure('Position', [10, 10, 800, 1000]);
plot(T,qd(:,1:4));
legend('q1','q2','q3','q4');
text(0.9,0.28,'\leftarrow q1');
legend('q1','q2','q3','q4');
grid on
不管习惯哪种画图，我们可以看到速度最终随着时间都变成了0，也就是机器人的机械臂在自身重力作用下都垂直向下静止了。
关节的角加速度
通过输入位姿、角速度、力矩来求角加速度
我们来看下各个关节的角加速度在qz位姿以及角速度和力矩为0的结果如下：
p560.accel(qz, zeros(1,6), zeros(1,6))
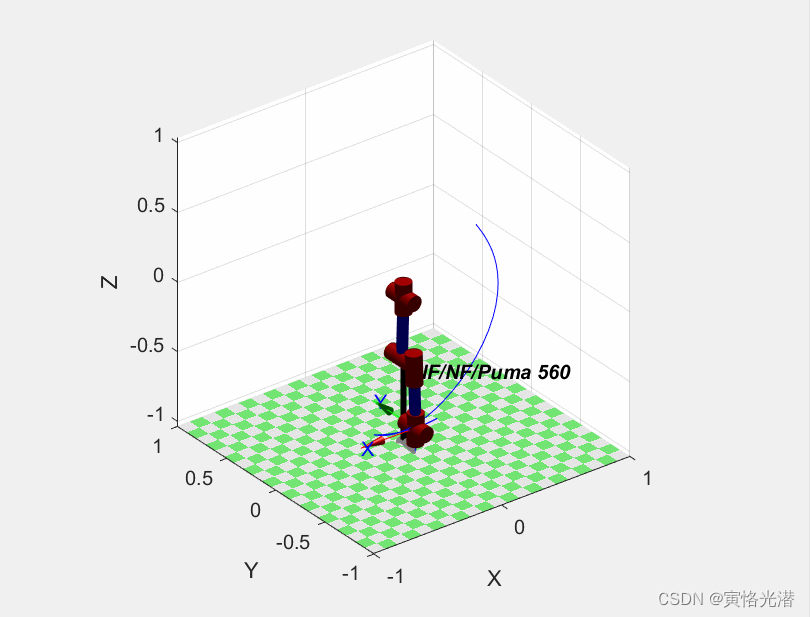
%结果分别为-0.2462,-8.682,3.146,0.002,0.0603,0.0001我们来演示下在重力作用下的机械臂的情况(这种保存动画更简单，而且可以将轨迹画出)：
p560.plot(q,'trail','b-','movie','r.gif')动图（由于超出5M大小，只能截图，最后静止状态）如下：
4、逆动力学Inverse dynamics
逆动力学，是根据物体所要达到的一定运动状态，求解作用在物体上的外力的方向和大小的学科。已知角度、角速度、角加速度等值，求解各关节所需提供的力。
关节力矩
力矩是力的大小乘以力臂的长度(牛顿*米)，所以我们拿扳手拧螺母的时候，扳手的力臂越长越轻松，因为力矩越大。
q1 = qn;%关节位姿
qd = [5 1 0 0 0 0]; %关节角速度
qdd = [0 0 0 0 0 0]; %关节角加速度
TAU = p560.rne(q1,qd,qdd);%求解逆向动力学
TAU =
22.1585 56.8861 -3.3693 -0.0018 0.0283 0.0002rne的参数选项
“gravity”G，指的是地心引力也就是重力加速度（默认[0,0,9.81]）。所以上面默认是：TAU = p560.rne(q,qd,qdd,[0,0,9.81]);
“fext”，W， 指定作用于末端执行器的扳手 W=[Fx Fy Fz Mx My Mz]
“slow”：不使用MEX文件
其余一些属性的求解如下 ：
%关节负载：
p560.gravload(q1)
ans =
-0.0000 31.6399 6.0351 0.0000 0.0283 0%空间惯性矩阵：
p560.inertia(qz)
ans =
3.9611 -0.1627 -0.1389 0.0016 -0.0004 0.0000
-0.1627 4.4566 0.3727 0.0000 0.0019 0.0000
-0.1389 0.3727 0.9387 0.0000 0.0019 0.0000
0.0016 0.0000 0.0000 0.1924 0.0000 0.0000
-0.0004 0.0019 0.0019 0.0000 0.1713 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000 0.1941%科氏力：
qd = [0.1 0.1 0.1 0.1 0.1 0.1];
p560.coriolis(qn,qd)%增加载荷质量：
R.payload(M, P) %在位置P增加一个质点为M的有效载荷
R.payload(0) %删除添加的有效载荷
%我们测试下：
p560.payload(1,[0 0.1 0.2])
%惯性矩阵：p560.inertia(qz)
ans =
4.1476 -0.1880 -0.1643 -0.0034 -0.0100 -0.0050
-0.1880 5.0224 0.7609 0.0632 0.1269 0.0632
-0.1643 0.7609 1.3188 0.0632 0.1269 0.0632
-0.0034 0.0632 0.0632 0.2024 0.0200 0.0100
-0.0100 0.1269 0.1269 0.0200 0.2113 0.0200
-0.0050 0.0632 0.0632 0.0100 0.0200 0.2041对比前面的惯性矩阵，我们可以看到矩阵的值在有外力的作用下发生了变化。
5、小结
关于摩擦力有几个简单解释下：
静摩擦力Static friction，Fs：静止时的摩擦力
库仑摩擦力Coulomb friction，Fc：静摩擦力+动摩擦力
黏性摩擦力Viscous friction，Fv：由于物体表面之间的黏性力而产生的摩擦力。比如关节与润滑油的摩擦，其摩擦力通常跟速度是非线性关系，只有物体的运动速度比较小的时候，就近似地看作其是关于速度线性的。
这里可以看到动力学跟运动学是有很大区别的，动力学是跟力有关系，使用的是牛顿三定律，根据受力分析可以得到物体的运动情况，或者反过来根据运动的情况来分析各种力的情况。而运动学是不考虑这些因素的，主要是运动的几何性质，空间变化。
