题目链接：leetcode使用最小花费爬楼梯

---

目录

题目解析：

算法原理

1.状态表示

2.状态转移方程

3.初始化

4.填表顺序

5.返回值

编写代码

---

题目解析：

题目让我们求达到楼梯顶部的最低花费.

由题可得：

 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用（每一阶所需的费用由cost[ ]里的值决定）。

可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，支付费用后，可选择向上爬一个或者两个台阶

那么楼顶在哪？

我们从题目里的实例一来分析：

如果楼顶是i，那么这里的最小花费为应该为10，但是这里输出是15

所以楼顶是在这里：

---

算法原理:

1.状态表示

先创建一个dp表

首先先思考dp表里面的值所表示的含义（是什么？）

dp[i]表示在到达i位置的最小花费

这种状态表示怎么来的？

1.经验+题目要求

经验：以i位置为结尾，

题目让我们求达到楼梯顶部的最低花费，那么这里我们可以dp[i]来表示。

所以这里我们用i表示楼顶；

2.状态转移方程

dp[i]等于什么？

用之前或者之后的状态，推导出dp[i]的值；

根据最近的最近的一步，来划分问题

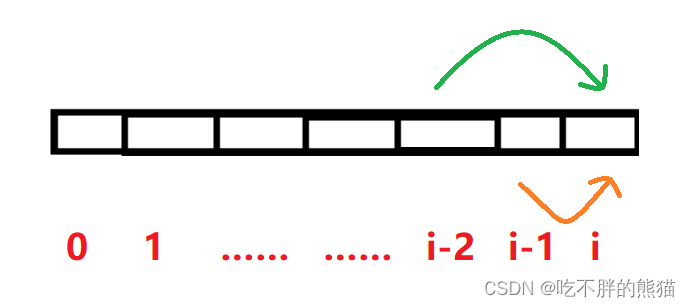
我们这里有两种情况：

第一种：

到达i-2是最小花费，支付cost[i-2]后跳两步到达楼顶；

第一种：

到达i-1是最小花费，支付cost[i-1]后跳一步到达楼顶；

所以：

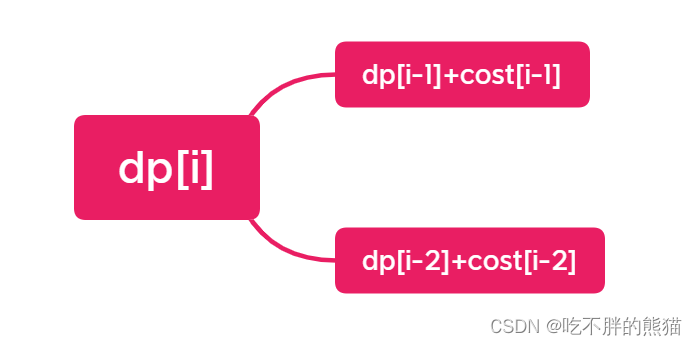
这里我们只要返回这两种情况的最小值就可以了

我们这里会用到min：

综上所述：

dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

3.初始化

(保证填表的时候不越界)

由题目得：

在第0，1阶的时候是不用花费的；

所以这里要初始化为0；

4.填表顺序

（为了填写当前状态的时候，所需要的状态已经计算过了）

这里所需要的状态是：dp[i-1]、dp[i-2]

这几个数都是在i之前的，

所以我们这里是从左向右填表；

5.返回值

（根据题目要求和状态表示）

综上分析：

返回值为：dp[n]

---

编写代码:

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
    //1.创建dp表
    //2.初始化
    //3.填表
    //4.返回结果

    int n=cost.size();
    vector <int> dp(n+1);
    //因为vector会把表里初始化为0，所以这里我们不用考虑初始化的情况

    for(int i=2;i<=n;i++)
    {
        dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
    }

    return dp[n];

    }
};