文心一言 VS 讯飞星火 VS chatgpt （154）-- 算法导论12.3 1题

news2024/10/6 6:05:12

一、用go语言，给出 TREE-INSERT 过程的一个递归版本。

文心一言，代码不能运行：

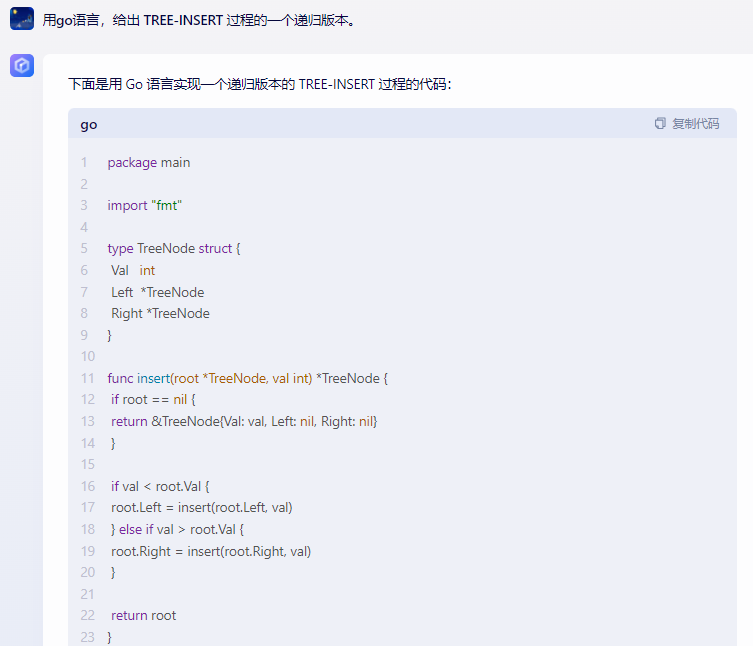
下面是用 Go 语言实现一个递归版本的 TREE-INSERT 过程的代码：

package main  
  
import "fmt"  
  
type TreeNode struct {  
 Val   int  
 Left  *TreeNode  
 Right *TreeNode  
}  
  
func insert(root *TreeNode, val int) *TreeNode {  
 if root == nil {  
 return &TreeNode{Val: val, Left: nil, Right: nil}  
 }  
  
 if val < root.Val {  
 root.Left = insert(root.Left, val)  
 } else if val > root.Val {  
 root.Right = insert(root.Right, val)  
 }  
  
 return root  
}  
  
func inorderTraversal(root *TreeNode) {  
 if root != nil {  
 inorderTraversal(root.Left)  
 fmt.Println(root.Val)  
 inorderTraversal(root.Right)  
 }  
}  
  
func main() {  
 root := nil  
 root = insert(root, 5)  
 insert(root, 3)  
 insert(root, 7)  
 insert(root, 1)  
 insert(root, 9)  
  
 inorderTraversal(root)  
}

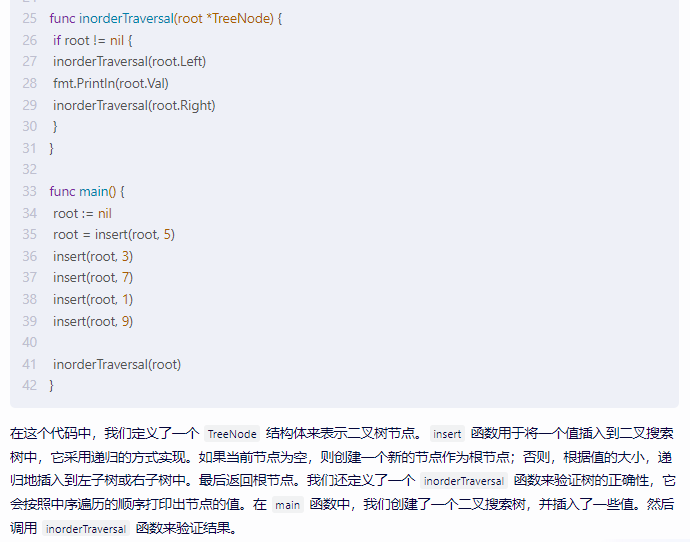
在这个代码中，我们定义了一个 TreeNode 结构体来表示二叉树节点。insert 函数用于将一个值插入到二叉搜索树中，它采用递归的方式实现。如果当前节点为空，则创建一个新的节点作为根节点；否则，根据值的大小，递归地插入到左子树或右子树中。最后返回根节点。我们还定义了一个 inorderTraversal 函数来验证树的正确性，它会按照中序遍历的顺序打印出节点的值。在 main 函数中，我们创建了一个二叉搜索树，并插入了一些值。然后调用 inorderTraversal 函数来验证结果。

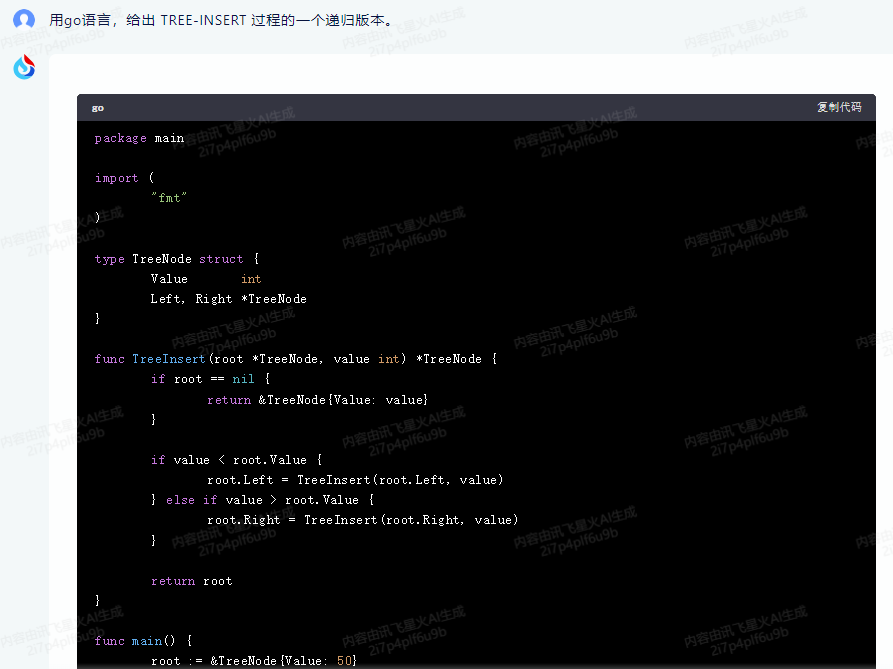
在这里插入图片描述

在这里插入图片描述

讯飞星火，代码正常运行：

package main

import (
	"fmt"
)

type TreeNode struct {
	Value       int
	Left, Right *TreeNode
}

func TreeInsert(root *TreeNode, value int) *TreeNode {
	if root == nil {
		return &TreeNode{Value: value}
	}

	if value < root.Value {
		root.Left = TreeInsert(root.Left, value)
	} else if value > root.Value {
		root.Right = TreeInsert(root.Right, value)
	}

	return root
}

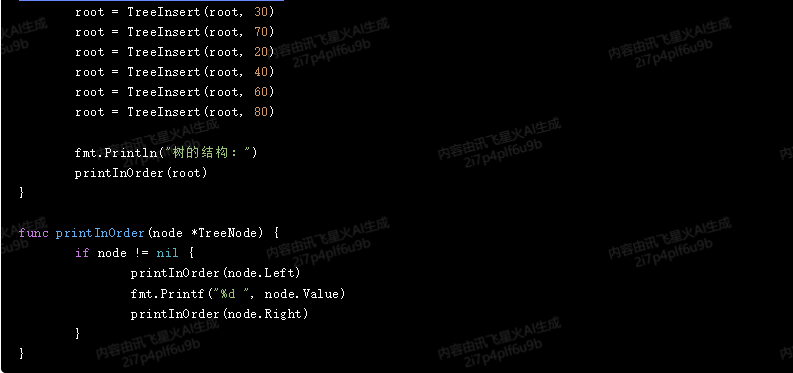
func main() {
	root := &TreeNode{Value: 50}
	root = TreeInsert(root, 30)
	root = TreeInsert(root, 70)
	root = TreeInsert(root, 20)
	root = TreeInsert(root, 40)
	root = TreeInsert(root, 60)
	root = TreeInsert(root, 80)

	fmt.Println("树的结构：")
	printInOrder(root)
}

func printInOrder(node *TreeNode) {
	if node != nil {
		printInOrder(node.Left)
		fmt.Printf("%d ", node.Value)
		printInOrder(node.Right)
	}
}

在这里插入图片描述

在这里插入图片描述

360智脑：

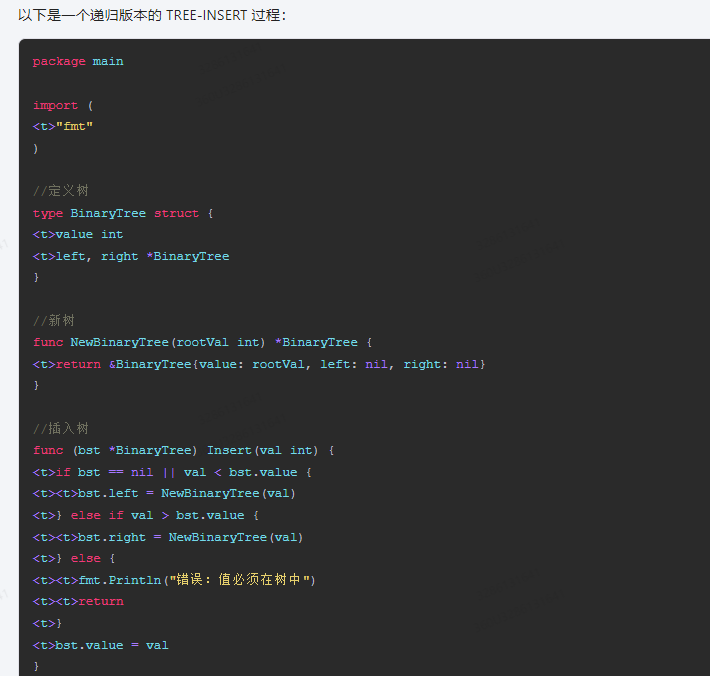
以下是一个递归版本的 TREE-INSERT 过程：

package main

import (
<t>"fmt"
)

//定义树
type BinaryTree struct {
<t>value int
<t>left, right *BinaryTree
}

//新树
func NewBinaryTree(rootVal int) *BinaryTree {
<t>return &BinaryTree{value: rootVal, left: nil, right: nil}
}

//插入树
func (bst *BinaryTree) Insert(val int) {
<t>if bst == nil || val < bst.value {
<t><t>bst.left = NewBinaryTree(val)
<t>} else if val > bst.value {
<t><t>bst.right = NewBinaryTree(val)
<t>} else {
<t><t>fmt.Println("错误：值必须在树中")
<t><t>return
<t>}
<t>bst.value = val
}

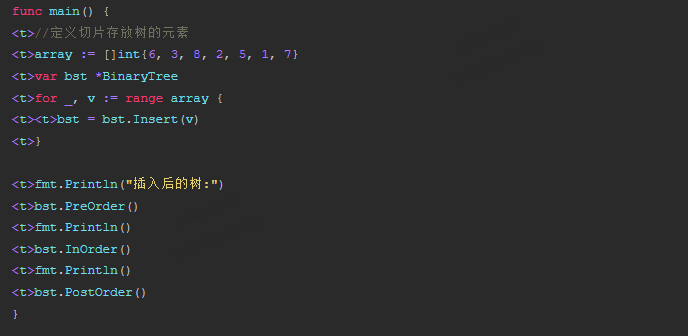
func main() {
<t>//定义切片存放树的元素
<t>array := []int{6, 3, 8, 2, 5, 1, 7}
<t>var bst *BinaryTree
<t>for _, v := range array {
<t><t>bst = bst.Insert(v)
<t>}

<t>fmt.Println("插入后的树:")
<t>bst.PreOrder()
<t>fmt.Println()
<t>bst.InOrder()
<t>fmt.Println()
<t>bst.PostOrder()
}

在这里插入图片描述

在这里插入图片描述

智谱清言，代码不能运行：

在计算机科学中，二叉搜索树（BST）是一种特殊的二叉树，它具有以下性质：

  • 每个节点都有一个作为关键字的值，该值唯一存在于树中。

  • 左子树上所有节点的值均小于它的根节点的值。

  • 右子树上所有节点的值均大于它的根节点的值。

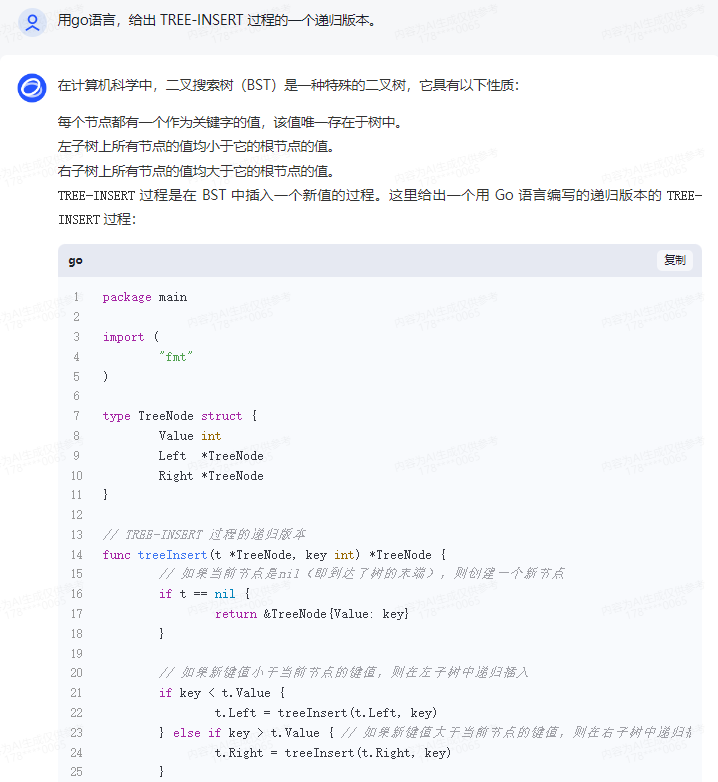
TREE-INSERT 过程是在 BST 中插入一个新值的过程。这里给出一个用 Go 语言编写的递归版本的 TREE-INSERT 过程：

package main
import (
	"fmt"
)
type TreeNode struct {
	Value int
	Left  *TreeNode
	Right *TreeNode
}
// TREE-INSERT 过程的递归版本
func treeInsert(t *TreeNode, key int) *TreeNode {
	// 如果当前节点是nil（即到达了树的末端），则创建一个新节点
	if t == nil {
		return &TreeNode{Value: key}
	}
	// 如果新键值小于当前节点的键值，则在左子树中递归插入
	if key < t.Value {
		t.Left = treeInsert(t.Left, key)
	} else if key > t.Value { // 如果新键值大于当前节点的键值，则在右子树中递归插入
		t.Right = treeInsert(t.Right, key)
	}
	// 返回当前节点（可能已经更新）
	return t
}
func main() {
	// 创建一个空的二叉搜索树
	root := nil
	// 向树中插入一些键值
	root = treeInsert(root, 5)
	root = treeInsert(root, 3)
	root = treeInsert(root, 8)
	root = treeInsert(root, 1)
	root = treeInsert(root, 4)
	root = treeInsert(root, 6)
	root = treeInsert(root, 9)
	root = treeInsert(root, 2)
	root = treeInsert(root, 7)
	// 以 inorder 遍历的方式打印树，验证是否正确插入
	var inorder func(t *TreeNode)
	inorder = func(t *TreeNode) {
		if t == nil {
			return
		}
		inorder(t.Left)
		fmt.Println(t.Value)
		inorder(t.Right)
	}
	// 开始 inorder 遍历
	inorder(root)
}

在这个代码中，treeInsert 函数以递归方式向 BST 中插入一个新值。如果当前节点是 nil，它将返回一个新节点。如果新值小于当前节点的值，它将在左子树中递归插入，如果新值大于当前节点的值，它将在右子树中递归插入。main 函数中展示了如何使用 treeInsert 函数，并通过 inorder 遍历打印出树的键值，以验证插入是否正确。

在这里插入图片描述

在这里插入图片描述

通义千问，代码正常运行：

在 Go 语言中，你可以使用递归来实现 TREE-INSERT 过程。这里是一个简单的示例，假设你有一个名为 Tree 的结构体表示二叉搜索树（BST）的节点，并且该结构体包含一个指向左子节点和右子节点的指针以及一个值。

package main

import "fmt"

type Tree struct {
    value int
    left  *Tree
    right *Tree
}

// Recursive TREE_INSERT function
func treeInsert(root **Tree, z *Tree) {
    if *root == nil {
        *root = z
        return
    }

    // Compare the new node's value with the current root's value
    if (*root).value > z.value {
        // If the new node's value is smaller, insert into the left subtree
        treeInsert(&(*root).left, z)
    } else {
        // If the new node's value is larger or equal, insert into the right subtree
        treeInsert(&(*root).right, z)
    }
}

func main() {
    var root *Tree
    z := &Tree{value: 10}
    treeInsert(&root, z)

    y := &Tree{value: 5}
    treeInsert(&root, y)

    x := &Tree{value: 15}
    treeInsert(&root, x)

    fmt.Println("In-order traversal:")
    inorderTraversal(root)
}

// Helper function to print in-order traversal of a binary search tree
func inorderTraversal(t *Tree) {
    if t != nil {
        inorderTraversal(t.left)
        fmt.Printf("%d ", t.value)
        inorderTraversal(t.right)
    }
}

在这个例子中，我们首先定义了一个 Tree 结构体来表示二叉搜索树的节点。接下来，我们实现了 treeInsert 函数，它接受一个指向树根的指针和一个新的节点 z。函数通过比较新节点的值与当前根节点的值来决定将新节点插入到左子树还是右子树。如果当前根为空，那么新节点就成为新的根节点。

在 main 函数中，我们创建了一个空的根节点，并使用 treeInsert 函数插入了几个新节点。最后，我们调用了一个辅助函数 inorderTraversal 来打印出二叉搜索树的中序遍历结果。

请注意，这个示例仅用于演示如何使用递归实现 TREE-INSERT 过程。在实际应用中，你需要根据你的具体需求对代码进行调整。

在这里插入图片描述

在这里插入图片描述

天工：

好的，以下是一个使用 Go 语言实现的 TREE-INSERT 过程的递归版本：

func TREE_INSERT(root *Node, z *Node) *Node {
    // 如果根节点为空，则创建一个新节点作为根节点
    if root == nil {
        root = &Node{key: z.key, val: z.val}
        return root
    }

    // 如果根节点的键小于 z 的键
    if root.key < z.key {
        // 将 z 插入到根节点的左子树中
        root.left = TREE_INSERT(root.left, z)
        return root
    }

    // 如果根节点的键等于 z 的键
    root.right = TREE_INSERT(root.right, z)

    // 返回根节点
    return root
}

其中，Node 结构体定义如下：

type Node struct {
    key int
    val int
    left *Node
    right *Node
}

该递归版本的实现思路与参考信息中的伪代码基本一致。当递归到叶子节点时，返回的根节点即为最后一个插入的元素。

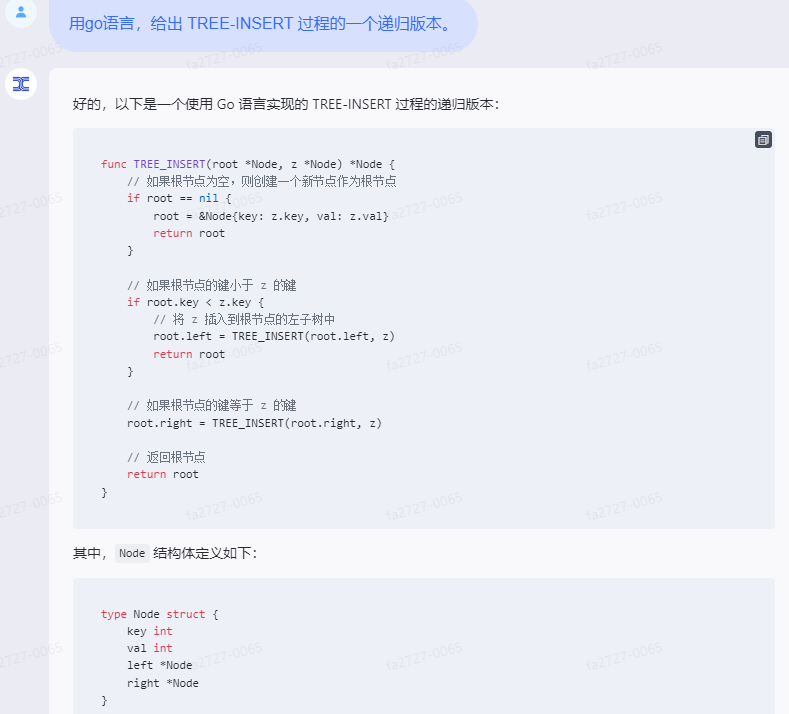
在这里插入图片描述

在这里插入图片描述

灵小智，代码正常运行：

以下是一个用Go语言编写的递归版本的TREE-INSERT过程示例：

package main

import "fmt"

type Node struct {
	key   int
	left  *Node
	right *Node
}

func insert(root *Node, key int) *Node {
	if root == nil {
		root = &Node{key: key, left: nil, right: nil}
		return root
	}

	if key < root.key {
		root.left = insert(root.left, key)
	} else if key > root.key {
		root.right = insert(root.right, key)
	}

	return root
}

func inorder(root *Node) {
	if root != nil {
		inorder(root.left)
		fmt.Printf("%d ", root.key)
		inorder(root.right)
	}
}

func main() {
	var root *Node

	keys := []int{15, 10, 20, 8, 12, 18, 25}

	for _, key := range keys {
		root = insert(root, key)
	}

	fmt.Println("Inorder traversal of the binary search tree:")
	inorder(root)
}

以上代码定义了一个名为Node的结构体，表示二叉搜索树中的节点。insert函数是一个递归函数，用于插入一个新的键值到二叉搜索树中。inorder函数用于按照中序遍历的顺序输出二叉搜索树中的节点。

在main函数中，我们创建一个空的二叉搜索树，并依次插入一些键值。最后，调用inorder函数打印二叉搜索树的中序遍历结果。

请注意，这只是一个示例，并没有涉及错误处理和其他边界情况的处理。实际使用时，您可能需要进行适当的错误处理和鲁棒性改进。

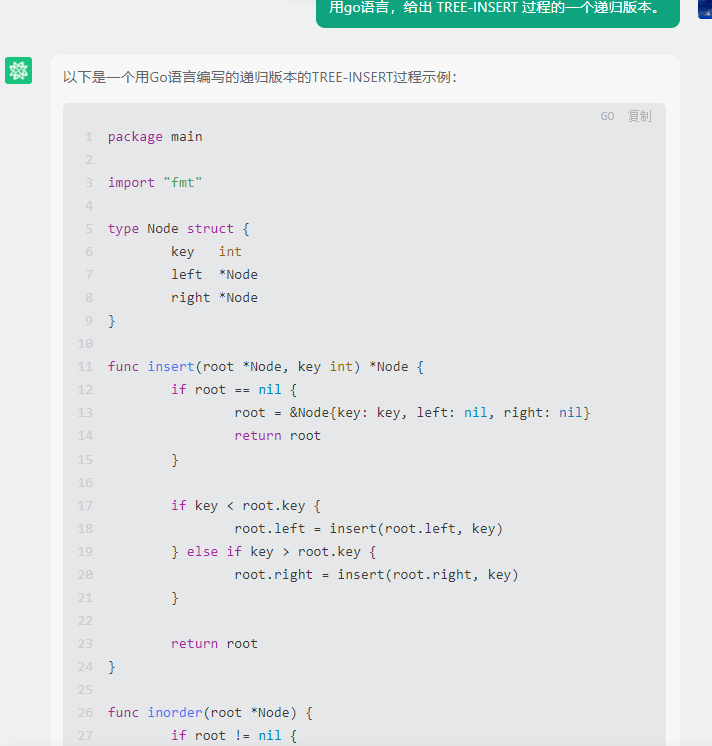
在这里插入图片描述

在这里插入图片描述

chatgpt：

以下是一个使用递归实现的TREE-INSERT过程的示例代码（假设节点数据类型为整数）：

type Node struct {
    key   int
    left  *Node
    right *Node
}

func insert(root *Node, key int) *Node {
    if root == nil {
        return &Node{key: key}
    }
    
    if key < root.key {
        root.left = insert(root.left, key)
    } else if key > root.key {
        root.right = insert(root.right, key)
    }
    
    return root
}

你可以将上述代码中的insert函数作为TREE-INSERT过程的递归版本。它会接收一个二叉搜索树的根节点和要插入的关键字作为参数，然后在树中递归地插入新节点，最终返回更新后的根节点。

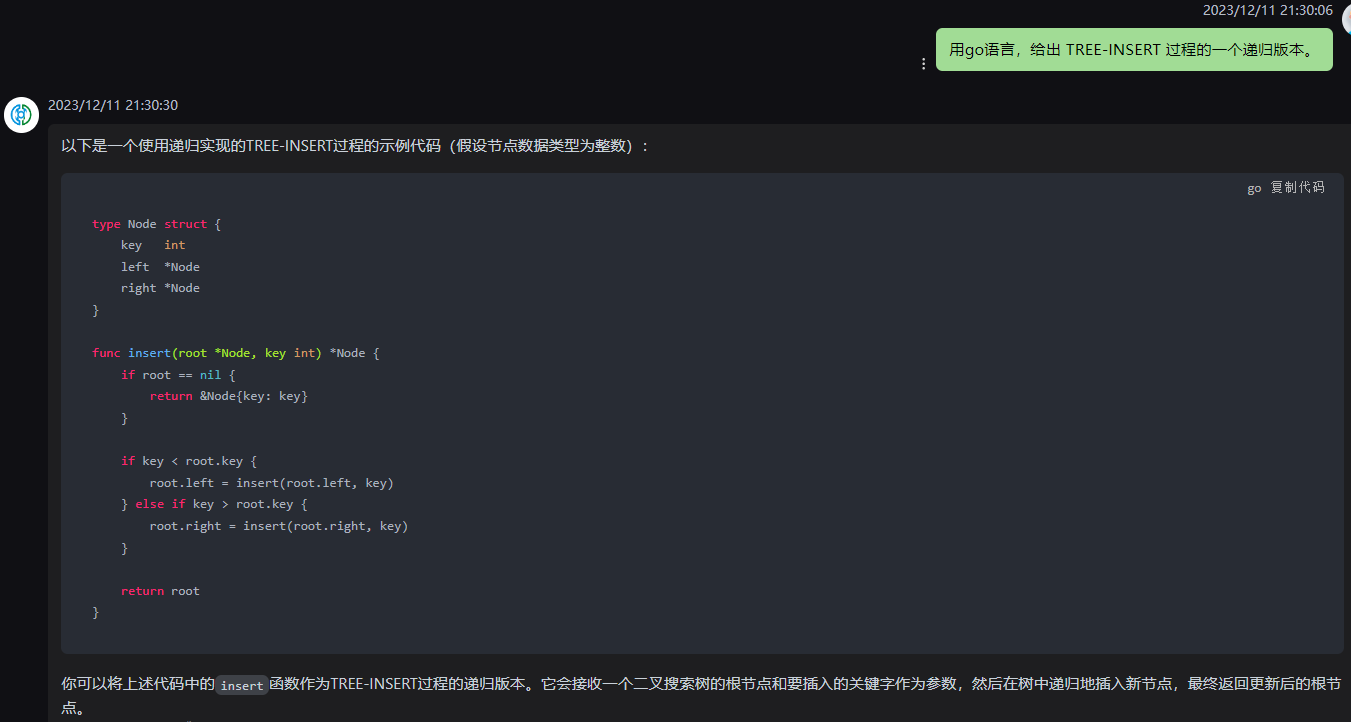
在这里插入图片描述

kimi，抛panic：

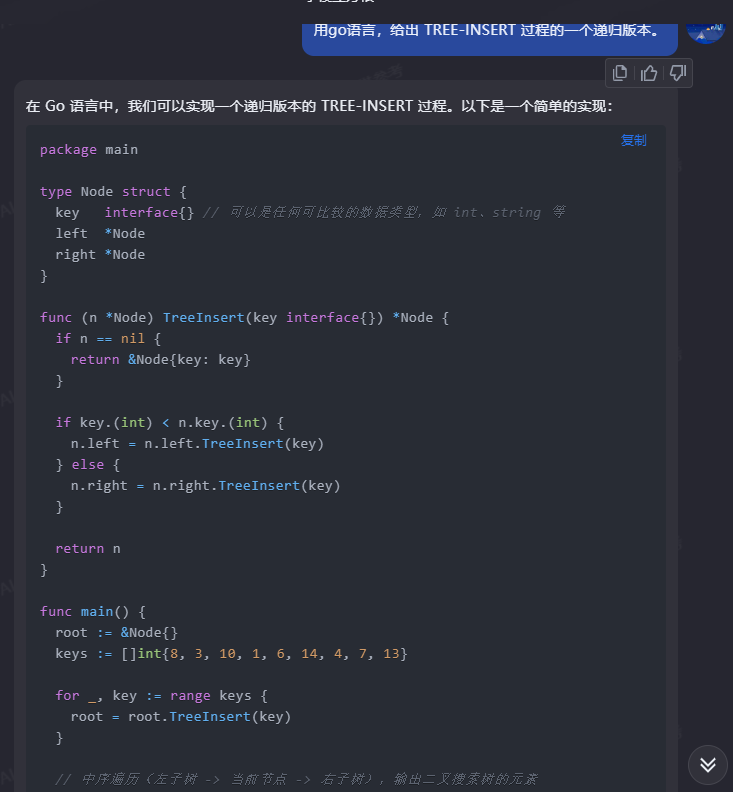
在 Go 语言中，我们可以实现一个递归版本的 TREE-INSERT 过程。以下是一个简单的实现：

package main

type Node struct {
	key   interface{} // 可以是任何可比较的数据类型，如 int、string 等
	left  *Node
	right *Node
}

func (n *Node) TreeInsert(key interface{}) *Node {
	if n == nil {
		return &Node{key: key}
	}

	if key.(int) < n.key.(int) {
		n.left = n.left.TreeInsert(key)
	} else {
		n.right = n.right.TreeInsert(key)
	}

	return n
}

func main() {
	root := &Node{}
	keys := []int{8, 3, 10, 1, 6, 14, 4, 7, 13}

	for _, key := range keys {
		root = root.TreeInsert(key)
	}

	// 中序遍历（左子树 -> 当前节点 -> 右子树），输出二叉搜索树的元素
	inOrderTraversal(root)
}

func inOrderTraversal(n *Node) {
	if n != nil {
		inOrderTraversal(n.left)
		fmt.Println(n.key)
		inOrderTraversal(n.right)
	}
}

在这个实现中，我们首先定义了一个 Node 结构体，表示二叉搜索树的节点。TreeInsert 方法是一个递归方法，它接受一个关键字作为参数。当树为空时，我们创建一个新的节点。然后，我们根据给定的关键字与当前节点的关键字的大小关系，将其插入到左子树或右子树中。

在 main 函数中，我们创建了一个空的根节点，并插入了一些整数。然后，我们使用 inOrderTraversal 函数按顺序遍历二叉搜索树并输出其元素。这个函数也是一个递归函数，它按照左子树 -> 当前节点 -> 右子树的顺序遍历树的节点。

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1303708.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

tiktok/抖音x-bogus参数分析

tiktok/抖音x-bogus参数分析

声明 本文以教学为基准、本文提供的可操作性不得用于任何商业用途和违法违规场景。 本人对任何原因在使用本人中提供的代码和策略时可能对用户自己或他人造成的任何形式的损失和伤害不承担责任。 如有侵权，请联系我进行删除。 这里只是我分析的分析过程，以及一些重要点的记录…
阅读更多...
web服务器之——www服务器的基本配置

web服务器之——www服务器的基本配置

目录 一、www简介 1、什么是www 2、www所用的协议 3、WEB服务器 4、主要数据 5、浏览器 二、 网址及HTTP简介 1、HTTP协议请求的工作流程 三、www服务器的类型(静态网站&#xff08;HTML&#xff09;&#xff0c; 动态网站(jsp python,php,perl)) 1、 仅提供…
阅读更多...
windows10安装MongoDB的入门简易教程【学习自用】

windows10安装MongoDB的入门简易教程【学习自用】

一、下载安装包 下载地址 https://www.mongodb.com/try/download/community 因为我是在windows上安装&#xff0c;所以下载windows版本的压缩包格式 二、下载后解压到要安装的目录里去 我这里在D盘装&#xff0c;所以就解压到D盘中我自己建的的mongoDB文件夹中。 三、在解…
阅读更多...
初识人工智能，一文读懂贝叶斯优化的知识文集(6)

初识人工智能，一文读懂贝叶斯优化的知识文集(6)

&#x1f3c6;作者简介&#xff0c;普修罗双战士&#xff0c;一直追求不断学习和成长&#xff0c;在技术的道路上持续探索和实践。 &#x1f3c6;多年互联网行业从业经验&#xff0c;历任核心研发工程师&#xff0c;项目技术负责人。 &#x1f389;欢迎 &#x1f44d;点赞✍评论…
阅读更多...
构建智能外卖跑腿小程序：技术实践与代码示例

构建智能外卖跑腿小程序：技术实践与代码示例

在快节奏的现代生活中&#xff0c;外卖跑腿服务已成为人们日常生活中不可或缺的一部分。为了提供更智能、高效的外卖跑腿体验&#xff0c;本文将深入探讨构建一款智能外卖跑腿小程序所需的关键技术&#xff0c;并提供相应的代码示例。 1. 地理位置服务的整合 外卖跑腿小程序…
阅读更多...
宇视科技视频监控 main-cgi 文件信息泄露漏洞复现

宇视科技视频监控 main-cgi 文件信息泄露漏洞复现

0x01 产品简介 宇视（Uniview）高清网络摄像机是一种高性能的网络摄像机，它可以通过网络进行视频传输和监控。该摄像机采用先进的视频技术，具有高清晰度、低照度、宽动态等特点，能够提供高质量的视频图像。 0x02 漏洞概述 宇视（Uniview）高清网络摄像机存在信息泄露漏洞…
阅读更多...
Android CoordinatorLayout

Android CoordinatorLayout

一、CoordinatorLayout CoordinatorLayout(协调者布局) 用于协调管理其子视图之间的交互行为。它旨在处理复杂的用户界面行为&#xff0c;允许子视图之间响应用户输入、动画和滚动等交互操作。 CoordinatorLayout 通过 Coordinator &#xff08;协调者&#xff09;来管理子视图…
阅读更多...
APD--传感器

APD--传感器

#1 Current temperature coeffiency Hamamastu Si APD S8664, with same bias, **low temperature**, **higher gain**, it means that **higher current output**. #2, PD
阅读更多...
Word插件-好用的插件-批量插入图片-大珩助手

Word插件-好用的插件-批量插入图片-大珩助手

现有100张图片&#xff0c;需要批量插入word中&#xff0c;并在word中以每页6张图片的形式呈现&#xff0c;请问怎样做&#xff1f; 使用word大珩助手&#xff0c;多媒体-插入图片&#xff0c;根据图片的长宽&#xff0c;选择连续图片、一行2个图或一行3个图&#xff0c;可一次…
阅读更多...
Web安全-SQL注入常用函数(二)

Web安全-SQL注入常用函数(二)

★★实战前置声明★★ 文章中涉及的程序(方法)可能带有攻击性&#xff0c;仅供安全研究与学习之用&#xff0c;读者将其信息做其他用途&#xff0c;由用户承担全部法律及连带责任&#xff0c;文章作者不承担任何法律及连带责任。 1、MySQL数据库构成 初始化安装MySQL数据库后(…
阅读更多...
web服务器之——搭建基于http协议的静态网站

web服务器之——搭建基于http协议的静态网站

目录 准备工作&#xff1a;web服务器搭建 第一步&#xff1a;挂载 第二步&#xff1a;编辑配置文件 第三步&#xff1a;安装软件包 第四步&#xff1a;启动httpd 查看配置文件&#xff1a; 第五步&#xff1a;设置防火墙状态&#xff1a; 重启服务: 查看状态&#xff…
阅读更多...
大致人类应该是短时记忆和利用短时记忆控制利用周围环境达到长期记忆的吧

大致人类应该是短时记忆和利用短时记忆控制利用周围环境达到长期记忆的吧

这里写目录标题 图代码代码解析图 代码 import timedef route_llm(route_text):passdef write_to_dask(one_sum, one_text, one_path
阅读更多...
【Mathtype】MathType符号面板没了或者变成可拖动如何解决

【Mathtype】MathType符号面板没了或者变成可拖动如何解决

1. MathType符号面板没了 如下图MathType符号面板没了&#xff0c;应该咋办&#xff1f; 向下面一样&#xff0c;在视图中选择工具栏即可 2. Mathtype符号面板可拖动如何还原 如下图所示&#xff0c;Mathtype变成了如下可以拖动的 直接选中工具栏的左上角&#xff0c;拖到…
阅读更多...
51单片机应用从零开始（十一）·数组函数、指针函数

51单片机应用从零开始（十一）·数组函数、指针函数

51单片机应用从零开始&#xff08;九&#xff09;数组-CSDN博客 51单片机应用从零开始&#xff08;十&#xff09;指针-CSDN博客 目录 1. 用数组作函数参数控制流水花样 2. 用指针作函数参数控制 P0 口 8 位 LED 流水点亮 1. 用数组作函数参数控制流水花样 要在51单片机中…
阅读更多...
探索 HTML 语义化：让你的网页更有意义(上)

探索 HTML 语义化：让你的网页更有意义(上)

&#x1f90d; 前端开发工程师&#xff08;主业&#xff09;、技术博主&#xff08;副业&#xff09;、已过CET6 &#x1f368; 阿珊和她的猫_CSDN个人主页 &#x1f560; 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 &#x1f35a; 蓝桥云课签约作者、已在蓝桥云…
阅读更多...
YOLOv8改进 | 主干篇 | SwinTransformer替换Backbone（附代码 + 详细修改步骤 +原理介绍）

YOLOv8改进 | 主干篇 | SwinTransformer替换Backbone（附代码 + 详细修改步骤 +原理介绍）

一、本文介绍 本文给大家带来的改进机制是利用Swin Transformer替换YOLOv8中的骨干网络其是一个开创性的视觉变换器模型&#xff0c;它通过使用位移窗口来构建分层的特征图&#xff0c;有效地适应了计算机视觉任务。与传统的变换器模型不同&#xff0c;Swin Transformer的自注…
阅读更多...
react中img引入本地图片的方式

react中img引入本地图片的方式

在html文件中&#xff0c;可以直接<img src./roadBook.png /> 但是在jsx文件中&#xff0c;不支持这种写法 必须这样写 在css样式中 App.css .img{background: url(./img/roadBook.png) }App.js import ./App.css;<div classNameimg></div> 1.基于es6Mod…
阅读更多...
UDS DTC故障码格式

UDS DTC故障码格式

文章目录 DTC的定义DTC 故障码的分类DTC 故障码的组成1、OBD DTC 格式结构2、UDS DTC&#xff08;ISO 14229-1、ISO 15031-6&#xff09;格式结构 参考 DTC的定义 DTC&#xff0c;Diagnostic Trouble Code&#xff0c;诊断故障码&#xff0c;即 故障类型的 ID。 一个完整的DT…
阅读更多...
N体问题-MATLAB 中的数值模拟

N体问题-MATLAB 中的数值模拟

一、说明 万有引力是宇宙普适真理&#xff0c;当计算两个物体的引力、质量、距离的关系是经典万有引力物理定律&#xff0c;然而面向复杂问题&#xff0c;比如出现三个以上物体的相互作用&#xff0c;随时间的运动力学&#xff0c;这种数学模型将是更高级的思维方法。本文将阐述…
阅读更多...
第二百零一回 介绍一个三方包open_settings

第二百零一回 介绍一个三方包open_settings

文章目录 1. 概念介绍2 使用方法3 代码与效果3.1 示例代码3.2 运行效果 4. 经验分享 我们在上一章回中介绍了Form Widget相关的内容&#xff0c;本章回中将介绍Form系列组件的验证与提交功能.闲话休提&#xff0c;让我们一起Talk Flutter吧。 1. 概念介绍 我们在这里说的的验…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023