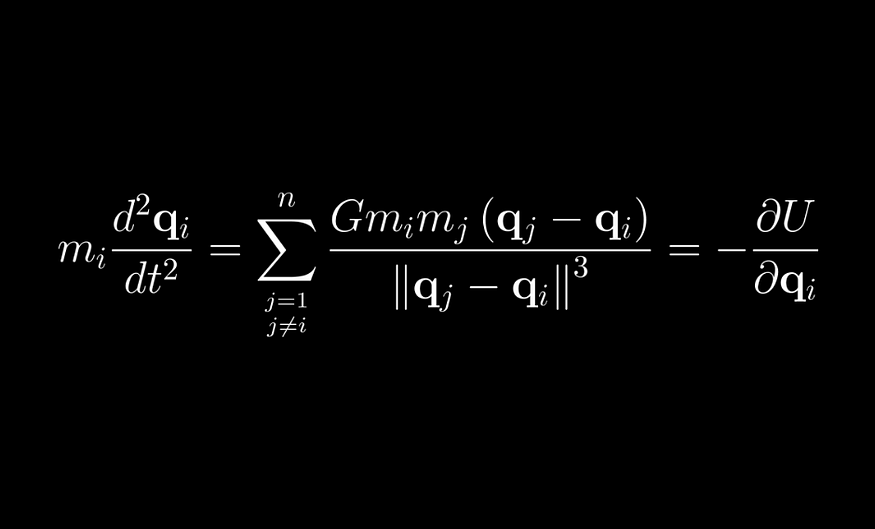
图片由作者提供。

二、关于万有引力模型

        牛顿在 17 世纪发现了万有引力，极大地改变了我们对天体运动的理解。他的定律巧妙地协调了两个深刻的物理原理：伽利略和笛卡尔在地球力学中提出的惯性原理，以及写在《新天文学》中的开普勒定律。

        牛顿在计算行星的轨道量时意识到他的万有引力定律并不完全准确。牛顿发现的不可预见的后果是对太阳系稳定的信念提出了质疑：行星一成不变地运动、没有碰撞或抛射的说法不再明显。由此，天文学家和几何学家之间展开了一场长达两个世纪的竞争，天文学家的观测越来越精确，几何学家掌握着牛顿定律的地位和命运。其核心是 N 体问题。

三、关于N体问题的讨论

        接下来，我们将创建N 个粒子通过共同引力势相互作用的模拟。庞加莱和布伦斯证明了该系统的微分方程一般不能以封闭形式积分（即用初等函数而不是无穷级数）。因此，如果我们想要进行任何有意义的模拟尝试，我们必须依靠数值方法。

        系统设置如下。我们假设N 个粒子索引为i = 1, 2, …, N，质量为 m_i，位置r ᵢ = [ xᵢ , yᵢ , zᵢ ]，速度v ᵢ = [v xᵢ , v yᵢ , v zᵢ ]。遵循牛顿万有引力定律，每个粒子都会感受到一种力

        其中G= 6.67×10^-11 m3/kg/s2 是万有引力常数。为了获得质量的加速度，我们将进行getAcceleration如下计算。

function [a] = getAcceleration(pos, mass, G, softening)
%   pos  is an N x 3 matrix of positions
%   mass is an N x 1 vector of masses
%   softening is the softening length
%   a is N x 3 matrix of accelerations

x = pos(:,1);
y = pos(:,2);
z = pos(:,3);
dx = x' - x;
dy = y' - y;
dz = z' - z;

% matrix that stores 1/r^3 for all particle pairwise particle separations
inverse = (dx.^2 + dy.^2 + dz.^2 + softening.^2).^(-3/2);

ax = G * (dx .* inverse) * mass;
ay = G * (dy .* inverse) * mass;
az = G * (dz .* inverse) * mass;

% pack together the acceleration components
a = [ax ay az];
end

        添加软化项是为了防止两个粒子彼此非常接近，在这种情况下，万有引力定律的加速度会达到无穷大。

        上面的代码是矢量化的。尽管在矩阵中存储中间计算需要大量内存，但它对于解释型语言非常有用；这有时会导致数十倍的加速。

        为了验证我们的代码，我们依靠能量守恒——我们知道这个量在时间演化中应该是恒定的。

        第一项是动能，定义为动量的平方除以质量的两倍。第二项是重力势能。我们的代码计算这些量并跟踪总能量，确保我们的近似值得到验证。

function [Ek, Ep] = getEnergy(pos, vel, mass, G)

% Kinetic Energy:
KE = 0.5 * sum(sum(mass.* vel.^2));

% Potential Energy:
% positions r = [x,y,z] for all particles
x = pos(:,1);
y = pos(:,2);
z = pos(:,3);

% matrix that stores all pairwise particle separations: r_j - r_i
dx = x' - x;
dy = y' - y;
dz = z' - z;

% matrix that stores r for all particle pairwise particle separations 
r = sqrt(dx.^2 + dy.^2 + dz.^2);

% sum over upper triangle, to count each interaction only once
PE = G *  sum(sum(triu(-(mass*mass')./r,1)));
end

        为了指定系统的初始条件，我们将从高斯分布中随机选择值。您可以使用 MATLAB 中的函数进行设置randn。

        对于数值积分，我们使用蛙跳方案，该方案采用踢-漂移-踢形式。

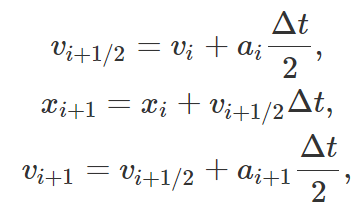
        演变是使用 for 循环在代码中执行的。

for i = 1:Nt
    vel = vel + acc * dt/2;
    pos = pos + vel * dt
    acc = getAcceleration(pos, mass, G, softening);
    vel = vel + acc * dt/2;
    t = t + dt;
end

        将加速度计算分离到步骤的开始和结束意味着如果时间分辨率增加两倍 (Δt →Δt/2)，则只需要一次额外的（计算成本较高的）加速度计算。

        当应用于力学问题时，跨越式积分有两个主要优势。首先是蛙跳法的时间可逆性。可以向前积分n步，然后反转积分方向，向后积分n步，以达到相同的起始位置。第二个优点是它的辛性质，有时允许动力系统的（稍微修改的）能量守恒（仅适用于某些简单系统）。这在计算轨道动力学时特别有用，因为许多其他积分方案（例如龙格-库塔方法）不保存能量并允许系统随时间大幅漂移。

        最后，我们使用另一个for循环，for i = 1:ceil(end_t/dt)运行蛙跳积分器并保存绘制轨迹的能量和位置。下面是我们的模拟结果。

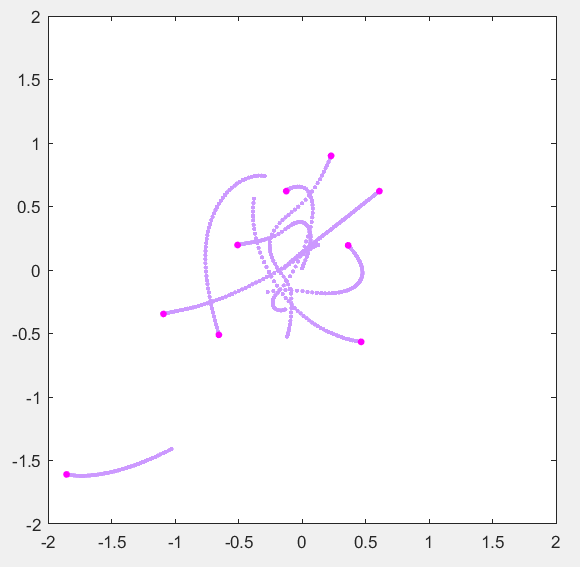
        N 体模拟 N = 10，dt = 0.01，软化 = 0.1。

在此处查找 GitHub 存储库。感谢您的阅读，祝您有美好的一天！