超参数优化在大多数机器学习流水线中已成为必不可少的一步，而贝叶斯优化则是最为广为人知的一种“学习”超参数优化方法。

超参数优化的任务旨在帮助选择学习算法中成本（或目标）函数的一组最佳参数。这些参数可以是数据驱动的（例如，各种训练数据组合）或模型驱动的（例如神经网络中的层数、学习率、优化器、批处理大小等）。在具有深度架构的最先进复杂机器学习模型中，由于参数的组合数以及这些参数之间的相互作用，超参数优化并不是一个简单的计算任务。

在本文中，我们将讨论贝叶斯优化作为一种具有记忆并从每次参数调整中学习的超参数优化方法。然后，我们将从头开始构建一个贝叶斯优化器，而不使用任何特定的库。

1. 为什么使用贝叶斯优化

传统的超参数优化方法，如网格搜索(grid search)和随机搜索(random search)，需要多次计算给定模型的成本函数，以找到超参数的最优组合。由于许多现代机器学习架构包含大量超参数（例如深度神经网络），计算成本函数变得计算昂贵，降低了传统方法（如网格搜索）的吸引力。在这种情况下，贝叶斯优化已成为常见的超参数优化方法之一，因为它能够在迭代次数明显较少的情况下找到优化的解决方案，相较于传统方法如网格搜索和随机搜索，这得益于从每次迭代中学习。

2. 贝叶斯优化的工作原理

贝叶斯优化在概念上可能看起来复杂，但一旦实现，它会变得更简单。在这一部分中，我将提供贝叶斯优化工作原理的概念性概述，然后我们将实施它以更好地理解。

贝叶斯优化利用贝叶斯技术对目标函数设置先验，然后添加一些新信息以得到后验函数。

先验表示在新信息可用之前我们所知道的内容，后验表示在给定新信息后我们对目标函数的了解。

更具体地说，收集搜索空间的样本（在这个上下文中是一组超参数），然后为给定样本计算目标函数（即训练和评估模型）。由于目标函数不容易获得，使用“替代函数”作为目标函数的贝叶斯近似。

然后，使用前一个样本的信息更新替代函数，从先验到后验。

后验表示在那个时间点上我们对目标函数的最佳了解，并用于指导“获取函数”。获取函数（例如期望改进）优化搜索空间内位置的条件概率，以获取更有可能优化原始成本函数的新样本。

继续使用期望改进的例子，获取函数计算超参数网格中每个点的期望改进，并返回具有最大值的点。然后，新收集的样本将通过成本函数运行，后验将被更新，这个过程重复，直到达到目标函数的可接受的优化点、产生足够好的结果，或者资源耗尽。

3. 实现

本节将专注于贝叶斯优化的逐步实现，共有七个步骤。首先，我将列出这些步骤，然后提供详细的解释，以及实现代码块。

• 导入库

• 定义目标（或成本）函数

• 定义参数边界

• 定义获取函数

• 初始化样本和替代函数

• 运行贝叶斯优化循环

• 返回结果

技术交流&材料获取

技术要学会分享、交流，不建议闭门造车。一个人可以走的很快、一堆人可以走的更远。

资料干货、资料分享、数据、技术交流提升，均可加交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

方式①、添加微信号：dkl88194，备注：来自CSDN + 资料
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复： 资料

1、数据分析实战宝典

2、100个超强算法模型

我们打造了《100个超强算法模型》，特点：从0到1轻松学习，原理、代码、案例应有尽有，所有的算法模型都是按照这样的节奏进行表述，所以是一套完完整整的案例库。

很多初学者是有这么一个痛点，就是案例，案例的完整性直接影响同学的兴致。因此，我整理了 100个最常见的算法模型，在你的学习路上助推一把！

让我们深入研究！

Step 1 — 导入库

我们首先导入一些必要的库，如下所示：

• numpy 用于数值计算，是数据科学中常见的库之一

• scipy.stats 是一个用于统计函数的库

• load_iris 是 scikit-learn 中加载鸢尾花数据集的函数

• GaussianProcessRegressor 是 scikit-learn 中实现高斯过程回归模型的类

• Matern 是 scikit-learn 中实现 Matern 核函数的类，用于高斯过程

import numpy as np
import scipy.stats as sps
from sklearn.datasets import load_iris
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import Matern

导入了这些库之后，让我们继续定义目标函数。

Step 2: 定义目标函数

目标函数接受一组超参数 C 和 gamma 作为输入，并返回在鸢尾花数据集上使用 RBF 核的支持向量分类器的负准确性。其中，C 是正则化参数，gamma 是 RBF、poly 和 sigmoid 核的核系数。核系数的详细信息对我们的流程并不关键，可以在这里找到。然后，我们使用 load_iris 加载鸢尾花数据集，并将数据分为训练集和测试集。数据准备好后，训练支持向量分类器，并返回在测试集上的负准确性。

def objective(params):
    C, gamma = params
    X, y = load_iris(return_X_y=True)
    np.random.seed(0)
    indices = np.random.permutation(len(X))
    X_train = X[indices[:100]]
    y_train = y[indices[:100]]
    X_test = X[indices[100:]]
    y_test = y[indices[100:]]
    from sklearn.svm import SVC
    clf = SVC(C=C, gamma=gamma)
    clf.fit(X_train, y_train)
    return -clf.score(X_test, y_test)

Step 3: 定义参数边界

在这一步，我们定义超参数搜索空间的边界。我们创建一个形状为 (2, 2) 的 NumPy 数组 bounds，其中每行对应一个超参数，每列对应该超参数的下界和上界。在我们的例子中，第一个超参数是 C，第二个是 gamma，两者都用于训练支持向量分类器。

设置边界的目的是限制超参数搜索空间，避免测试不太可能是最优的值，并将优化焦点放在超参数空间的最有希望的区域。我们对这个练习随机定义了边界，但在超参数范围已知的任务中，这变得很重要。

bounds = np.array([[1e-3, 1e3], [1e-5, 1e-1]])

Step 4: 定义获取函数

这一步定义了我们之前讨论过的获取函数，并确定在搜索空间中要评估的下一个点。在这个具体的例子中，获取函数是期望改进（Expected Improvement, EI）函数。它测量目标函数在当前最佳观测值的基础上的期望改进，考虑到当前替代模型（高斯过程）。获取函数的定义如下：

• 高斯过程使用 gp.predict() 在点 x 处预测均值和标准差。

• 函数找到迄今为止观察到的最佳目标函数值（f_best）。

• 计算对 f_best 的改进为 improvement = f_best — mu。

• 如果 sigma 为正，则计算标准得分 Z = improvement/sigma；如果 sigma 为 0，则将 Z 设置为 0。

• 使用标准正态分布的累积分布函数（sps.norm.cdf）和概率密度函数（sps.norm.pdf）计算在点 x 处的期望改进（ei）。

• 返回期望改进。

def acquisition(x):
    mu, sigma = gp.predict(x.reshape(1, -1), return_std=True)
    f_best = np.min(y_samples)
    improvement = f_best - mu
    with np.errstate(divide='warn'):
        Z = improvement / sigma if sigma > 0 else 0
        ei = improvement * sps.norm.cdf(Z) + sigma * sps.norm.pdf(Z)
        ei[sigma == 0.0] == 0.0
    return ei

Step 5: 初始化样本和替代函数

在开始贝叶斯优化循环之前，我们需要使用一些初始样本初始化高斯过程替代模型。如前所述，替代函数用于有效地逼近未知的目标函数以进行优化。高斯过程是一个概率模型，定义了对函数的先验。随着获取新数据，它允许使用贝叶斯推理来更新模型。具体而言，x_samples 是从由 bounds 数组定义的搜索空间中随机抽样的初始点。y_samples 是这些初始点对应的目标函数评估。这些样本用于训练高斯过程，并改进其替代建模。

Step 6: 运行贝叶斯优化循环

我们终于来到了贝叶斯优化循环。在这一步中，贝叶斯优化循环将运行指定次数（n_iter）。在每次迭代中，使用现有样本（即 x_samples 和 y_samples）更新高斯过程模型，使用 gp.fit() 方法。然后，通过在参数空间生成的大量随机点（即 x_random_points）优化获取函数，选择下一个由目标函数评估的样本。在这些点上评估获取函数，并选择获取函数值最大的点作为下一个样本（即 x_next）。在此点记录获取函数值作为 best_acq_value。最后，在选择的点上评估目标函数，并通过更新 x_samples 和 y_samples 将结果值添加到现有样本中。这个过程重复进行指定次数的迭代（即 n_iter），并打印每次迭代的结果。

# 运行 n_iter 次的贝叶斯优化循环
n_iter = 10
for i in range(n_iter):
    # 使用现有样本更新高斯过程
    gp.fit(x_samples, y_samples)

    # 通过优化获取函数找到下一个样本
    x_next = None
    best_acq_value = -np.inf

    # 从参数空间中抽样大量随机点
    n_random_points = 10000
    x_random_points = np.random.uniform(bounds[:, 0], bounds[:, 1], size=(n_random_points, bounds.shape[0]))

    # 在每个点上评估获取函数并找到最大值
    acq_values = np.array([acquisition(x) for x in x_random_points])
    max_acq_index = np.argmax(acq_values)
    max_acq_value = acq_values[max_acq_index]

    if max_acq_value > best_acq_value:
        best_acq_value = max_acq_value
        x_next = x_random_points[max_acq_index]

    print(f"Iteration {i+1}: next sample is {x_next}, acquisition value is {best_acq_value}")

    # 在下一个样本上评估目标函数并将其添加到现有样本中
    y_next = objective(x_next)
    x_samples = np.vstack((x_samples, x_next))
    y_samples = np.append(y_samples, y_next)

Step 7: 打印结果

最后，我们打印在贝叶斯优化循环中找到的最佳参数和最佳准确性。最佳参数是与目标函数最小值相对应的参数，这就是为什么使用 np.argmin 来找到 y_samples 最小值的索引。

# Print final results   
best_index = np.argmin(y_samples)   
best_x = x_samples[best_index]   
best_y = y_samples[best_index]   

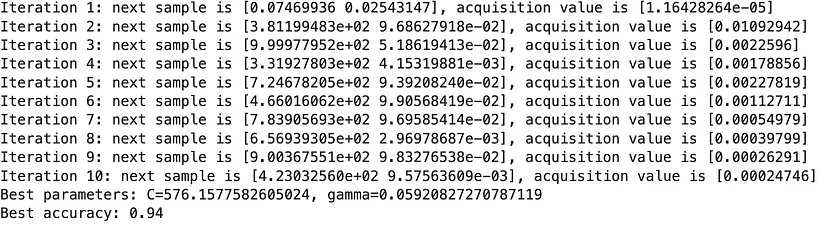
print(f"Best parameters: C={best_x[0]}, gamma={best_x[1]}")   
print(f"Best accuracy: {best_y}")

以下是运行此过程的最终结果：

4. 结论

在本文中，我们介绍了机器学习流水线中的超参数优化，并深入探讨了超参数优化的世界，详细讨论了贝叶斯优化以及为什么它可能是一种相对于基本优化器（如网格搜索和随机搜索）更有效的微调策略。然后，我们逐步从头开始构建了一个用于分类的贝叶斯优化器，以更好地理解这个过程。