二进制差异序列（格雷码）

Description

n 位二进制差异序列是一个由2^n个整数组成的序列，其中：
每个整数都在范围[0, 2^n - 1]内（含0和2^n - 1）
第一个整数是0
一个整数在序列中出现不超过一次
每对相邻整数的二进制表示恰好一位不同，且
第一个和最后一个整数的二进制表示恰好一位不同
给你一个整数n，返回任一有效的n位二进制差异序列，1≤n ≤ 16

Input

输入一个整数n

Output

输出二进制差异序列，每个数之间空格隔开

Sample

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int powN = (int) Math.pow(2, n);
        int[] grayCode = new int[powN];
        for (int i = 0; i < powN; i++) {
            grayCode[i] = toGrayCode(i);
            System.out.print(grayCode[i] + " ");
        }
    }

    public static int toGrayCode(int i) {
        return i ^ (i >> 1);
    }


}

思路

首先，n位对应的格雷码不止一个
因此只需要找到一个格雷码输出即可

格雷码跟8421码一样，也是一种对数字进行二进制编码的方法，只是编码方法跟常见的8421二进制编码方法不一样。
例如：
n = 3 的 8421 编码和选取的一组格雷码

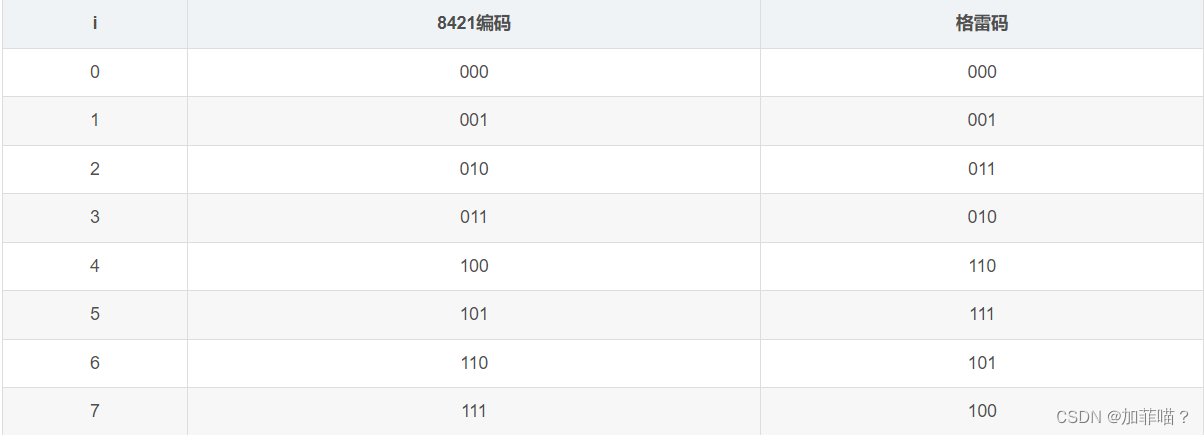
可以通过这组观察出特殊的规律
1、8421码最左边一位不变，保留下来成为格雷码的最左边一位；
2、从左边第二位开始，将8421码的每一位与它左边的一位相 异或 得到对应位的格雷码；
3.也就是将其与其右移一位进行异或操作（正数右移左补0）
因此可以采取

/**
*i指0-2^n数字
*/
int graycode = i ^ (i >> 1);