代码随想录 (programmercarl.com)

理论基础

一、题目类型：

动规基础、背包问题、打家劫舍、股票买卖、子序列问题

二、解题思路：

动态规划五部曲：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

509.斐波那契数

一、递归解法：

class Solution {
    public int fib(int n) {
        int num = 0;
        if (n <= 1){
            return n;
        } else {
            num = fib(n - 1) + fib(n - 2);
        }
        return num;
    }
}

二、动态规划思路：

确定dp数组（dp table）以及下标的含义

        dp[i]:第i个斐波那契数值

确定递推公式

        dp[i] = dp[i - 1] + dp[i - 2]

dp数组如何初始化

        dp[0] = 0,  dp[1] = 1

确定遍历顺序

        从前向后遍历

举例推导dp数组/打印dp数组

class Solution {
    public int fib(int n) {
        if (n <= 1){
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0; dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

此处创建的数组长度为n + 1，数组里面存放的是每个数的斐波那契值

70.爬楼梯

一、递归解法：

本质和上一题的斐波那契数列一样

class Solution {
    public int climbStairs(int n) {
        int res = 0;
        if (n <= 2){
            return n;
        }else {
            res = climbStairs(n - 1) + climbStairs(n - 2);
        }
        return res;
    }
}

力扣运行超出时间限制

二、动态规划思路：

确定dp数组（dp table）以及下标的含义

        dp[i]:到达第i阶，共有dp[i]种方法

确定递推公式

        dp[i] = dp[i - 1] + dp[i - 2]

dp数组如何初始化

        dp[1] = 1,  dp[2] = 2

//直接初始化dp[0]和dp[1]，和上一题代码几乎一致

确定遍历顺序

        从前向后遍历

举例推导dp数组/打印dp数组

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1; dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

三、用变量代替数组：

// 用变量记录代替数组
class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        int a = 1, b = 2, sum = 0;

        for(int i = 3; i <= n; i++){
            sum = a + b;  // f(i - 1) + f(i - 2)
            a = b;        // 记录f(i - 1)，即下一轮的f(i - 2)
            b = sum;      // 记录f(i)，即下一轮的f(i - 1)
        }
        return b;
    }
}

746.使用最小花费爬楼梯 

确定dp数组（dp table）以及下标的含义

        dp[i]:到达i位置所需要的最小花费dp[i]

确定递推公式

        dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])

dp数组如何初始化

       你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯，所以二者的初始化都为0

        dp[0] = 0,  dp[1] = 0

确定遍历顺序

        从前向后遍历

举例推导dp数组/打印dp数组

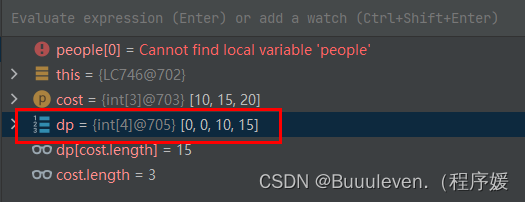
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length + 1];
        dp[0] = 0; dp[1] = 0;
        for (int i = 2; i <= cost.length; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.length];
    }
}