课程回顾

基础知识

• 回归分析是研究变量之间相互依赖关系得一种统计方法。通过回归分析，将不确定的相关关系转变为确定的函数函数关系进行表达。
  
• 均值回归：Y的数学期望是可以由X进行唯一确定，数学期望之间的函数关系
  

回归模型的建模过程

• 选取模型的变量：找到相互影响的变量
• 收集整理统计数据：做实验收集数据
• 回归模型的选取：
  • 函数f（x）的选取
  • 随机变量的类型
• 模型的参数估计
  • 判定选取的参数优良性，就像拟合问题中差值，插值函数中插值余项
• 模型的检验
  • 检验算出来的模型，是否能用
• 模型的应用：预测与控制

一元线性回归模型

• 模型的假定：均值回归，是Y的期望和x的函数关系，Y和x并没有函数关系

• 基于样本的抽样分布，去估计整体的抽样分布。需要知道整体是什么抽样分布。假设分布
  

线性回顾进行极大似然估计（例题（必考））

• 要求：总体分布已知，去找总体分布的极大似然估计。

极大似然估计

• 写出总体的密度函数，这里很多关于密度函数的东西不是很清楚，需要单独记一下。总体的密度函数，似然函数应该是n个密度函数的乘积。

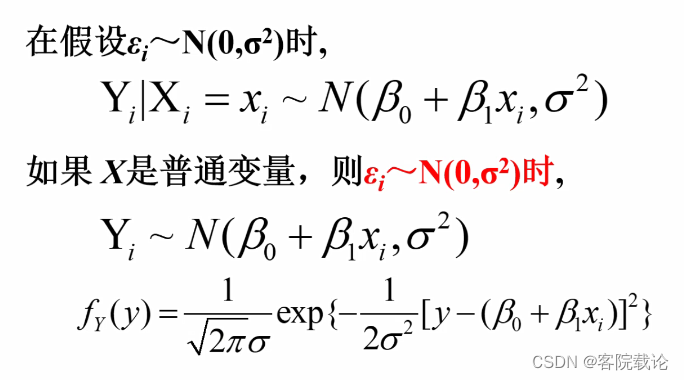
• n个整体的密度函数进行的乘积，就是似然函数，象征着抽样结果本身发生的可能性大小。
  

• 求出似然函数的最大值，一般是求取对数似然函数的最大值点，（xi，yi）是样本的观测值，β和σ是需要求取的值 。在正态估计下，最小二乘和极大似然估计的结果是相同的。

• 因为似然函数是连乘，不便于求解，所以使用对数，方便求解
  

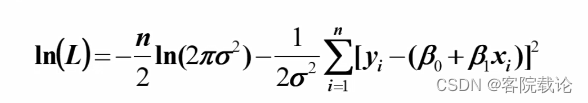
• 对数似然函数求偏导，求似然函数的最大值点，原来是求取驻点。

• 要把对数似然函数，分别对β1和β0求一阶偏导。

• 求残差平方和的最小值点，等价于最小二乘法。
  

• 注意：

  • 期末考试可能会同时考，虽然结果可能是一样的，但是方法是不一样的，两者的含义也不同
  • 线性最小二乘：求超定方程组解，在残差平方和的损失下，求取最优解
  • 极大似然估计：在整体分布已知的情况下，去估计分布参数，在正态假设下，和最小二乘的方法完全相同。

• 求解过程
  
  

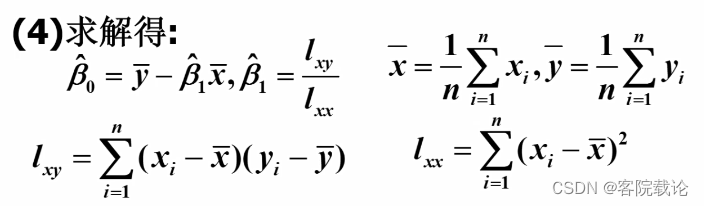
极大似然估计的性质

线性性

• 估计量β1和β0为随机变量yi的线性函数
  
  
• β1和β0都可以化为yi的线性变量

无偏性

• β1一肩和β0一肩的数学期望相应的都是β1和β0，成为无偏估计
  

最优性（记住即可，没有推导）

• 在线性无偏估计的情况下，最小二乘估计方差最小，所有是最优线性无偏估计。
  

方差计算

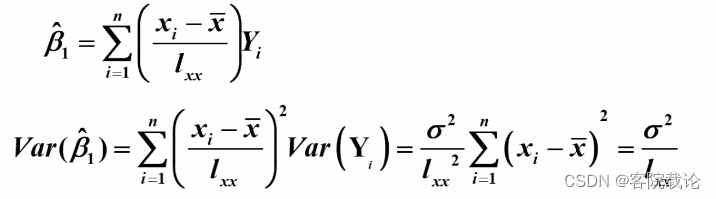
• σ是整体的方差，整体的方差越大，说明考虑变量的时候将影响力较大的变量放到了∑中，没有作为主要变量进行考虑
• lxx表示采样数据的密集程度，如果采样数据越密集，那么方差就越大，数据就越差。

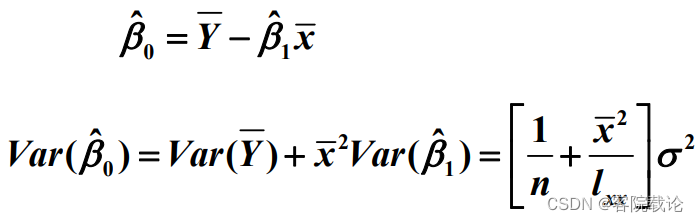
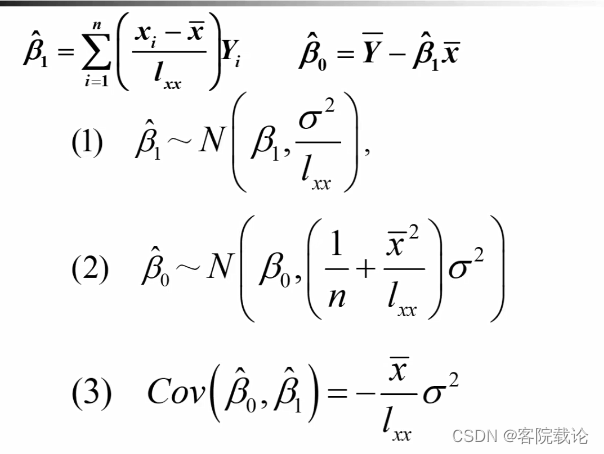
一元线性回归模型的检验

参数检验

拟合优先度

• 通过参数指标检验，仅仅作为了解即可
• 总平方和（SST）
  • 反应因变量的n观察值与其均值的总离差
• 回归平方和（SSR）（X贡献的影响）
  • 反应自变量x的变化对于因变量y取值变化的影响，或者说，是由于x与y之间线性关系引起的y的取值变化，反映了自变量x的重要性
• 残差平方和（SSE）（除了x之外的贡献的影响）
  • 反应除了x意外的其他因素对于y取值的影响，称为不可解释的平方和或者剩余平方和
• 总结：
  • 残差平方和越小越好，回归平方和越大越好
    
    
• 拟合有限度可以解释变量和结果拟合程度，越靠近一，拟合程度越高。

相关系数检验（回归之前的计算）

• 表示样本相关系数，样本背后变量y和x之间的线性相关程度。

显著性检验（明白最基本的想法即可，不考）

t检验

• 在原假设的前提下构建对应分布

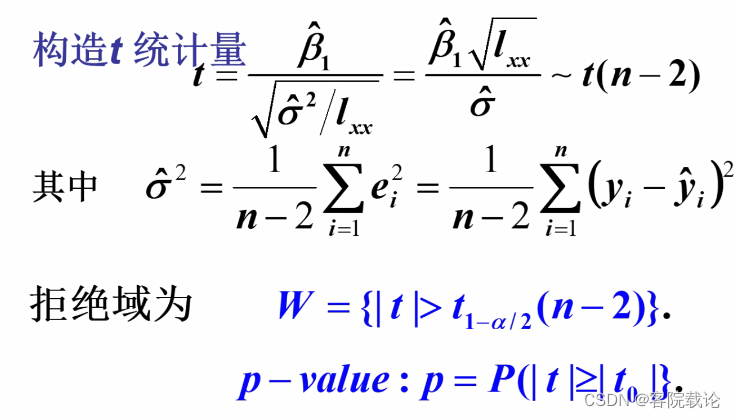
• 通过拒绝域或者p-value来看是否拒绝原假设。

F检验

回归模型的预测

点值预测

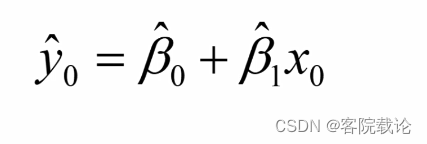
区间估计

• 因变量新值得区间预测
  
• 计算出y0一肩的分布，然后根据已知分布获取概率区间

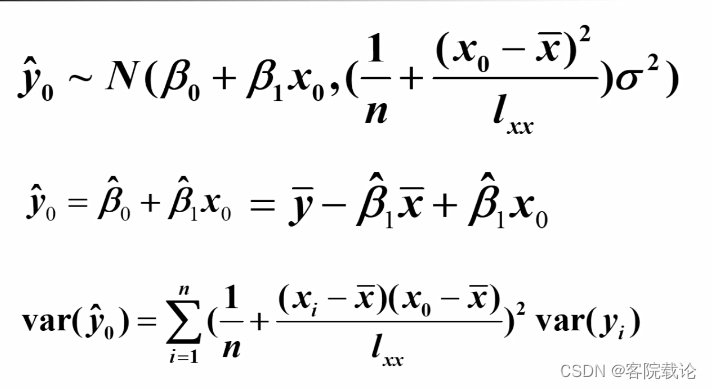
• 去除未知量σ的平方
  
  
  

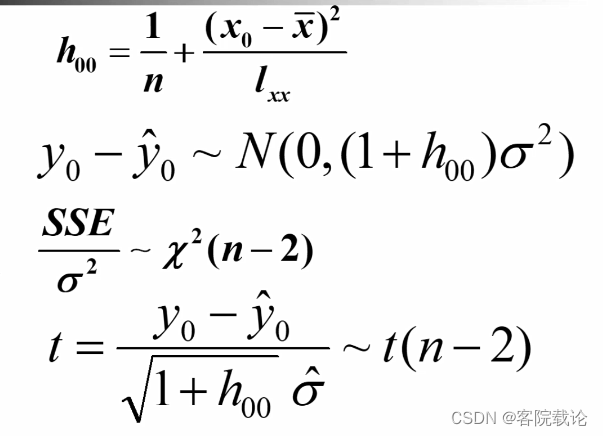
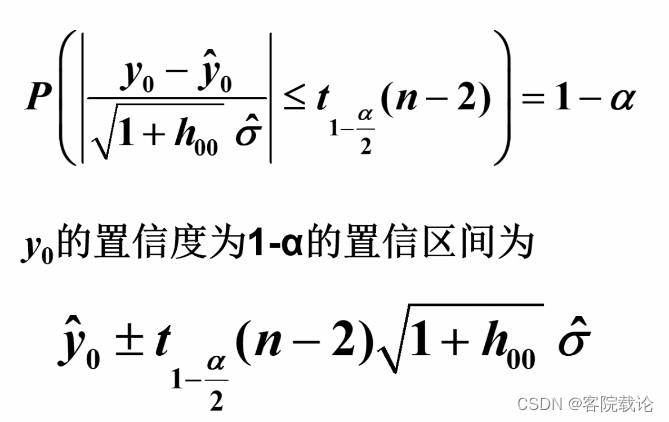
• n越大，区间长度越短，回归效果越好。

• 预测数据和采样数据差异越大，区间长度越长，回归效果越差

控制问题

• 如何选择x的值，才能确保最终的结果在1-α的范围内。左右两边相等，注意符号。
  
  

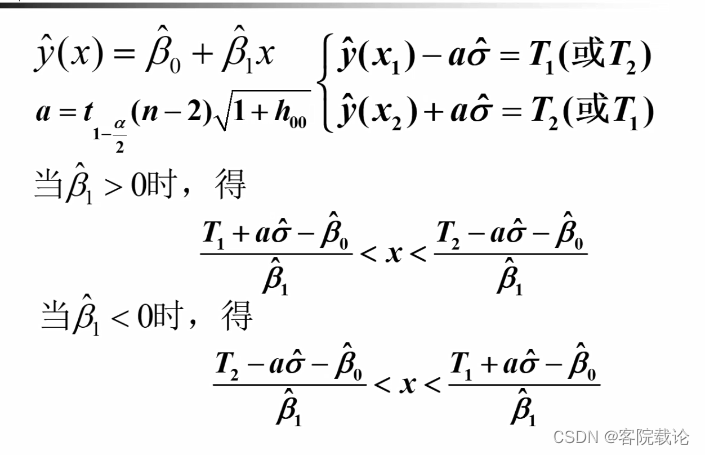
一元回归模型分析样例（必会）

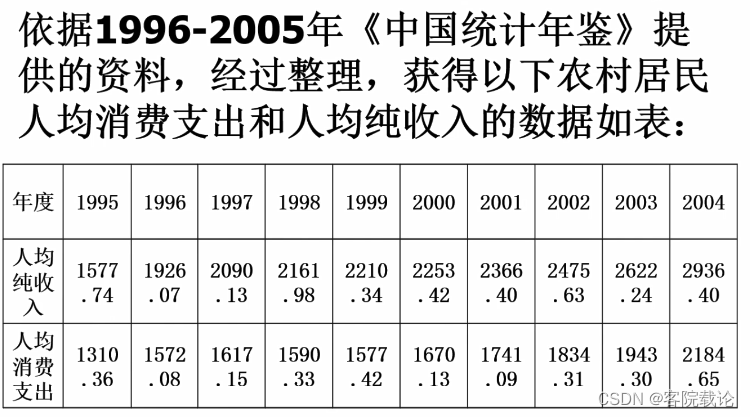
• 选择线性回归模型，看作是均值回归，一次函数，看作是正态假设。
• 建立模型
  
  

模型检验

T检验

预测

总结

• 线性回归和线性拟合进行综合考试，第一问会做线性拟合，使用最小二乘法，第二小问会考线性回归，使用极大似然估计。