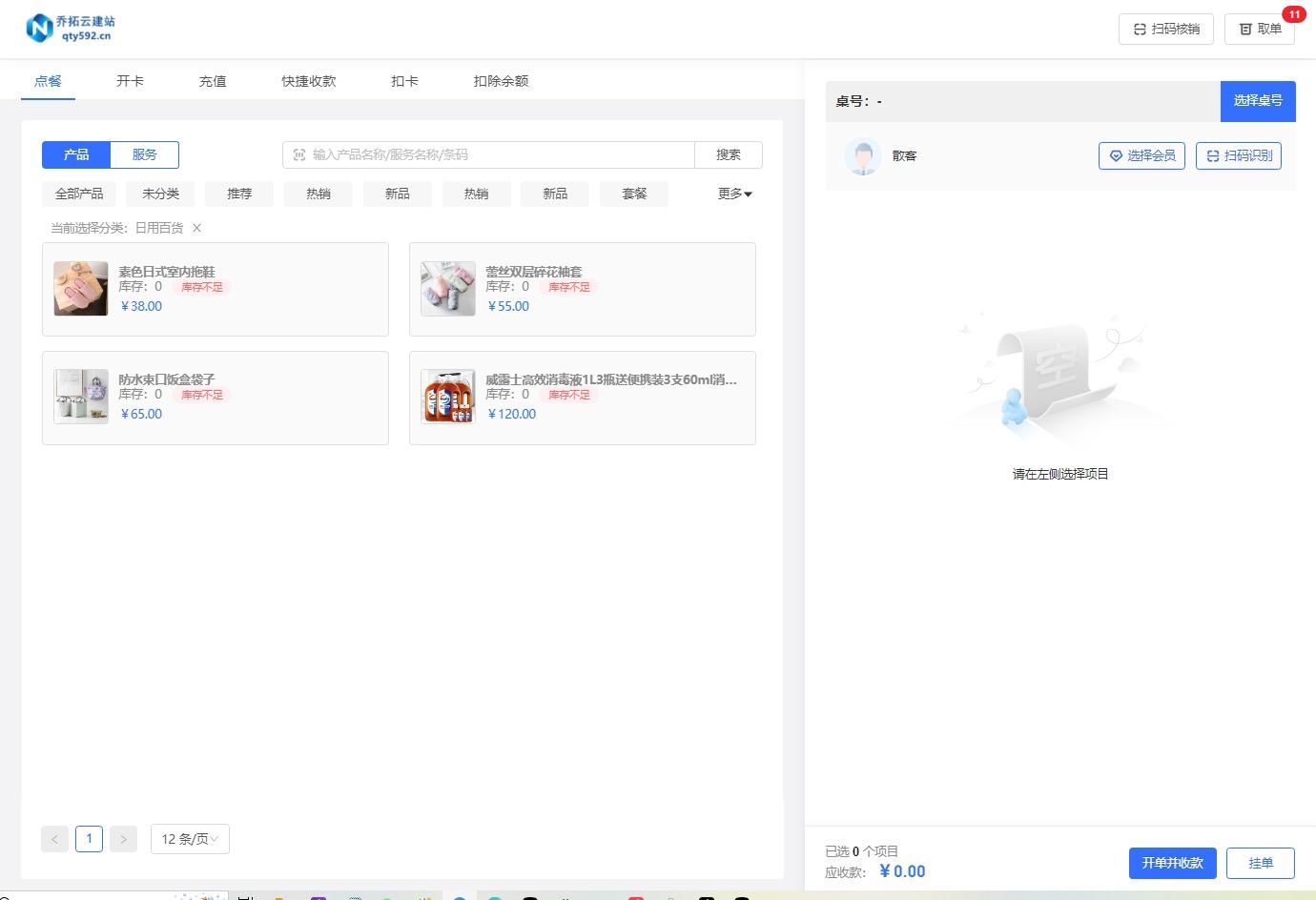
关卡名	理解与贪心有关的高频问题	我会了✔️
内容	1.理解跳跃游戏问题如何判断是否能到达终点	✔️
	2.如果能到终点，如何确定最少跳跃次数	✔️

1. 跳跃游戏 

leetCode 55 给定一个非负整数数组，你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度，判断你是否能够到达最后一个位置。

示例1：

输入: [2,3,1,1,4]

输出: true

解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。

示例2：

输入: [3,2,1,0,4]

输出: false

解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ，所以你永远不可能到达最后一个位置。

如果当前位置元素如果是3，我究竟是跳几步呢，一步，两步，还是三步？这里的关键是判断能否到达终点，不用每一步跳跃到哪个位置，而是尽可能的跳跃到最远的位置，看最多能覆盖到哪里，只要不断更新能覆盖的距离，最后能覆盖到末尾就行了。

 

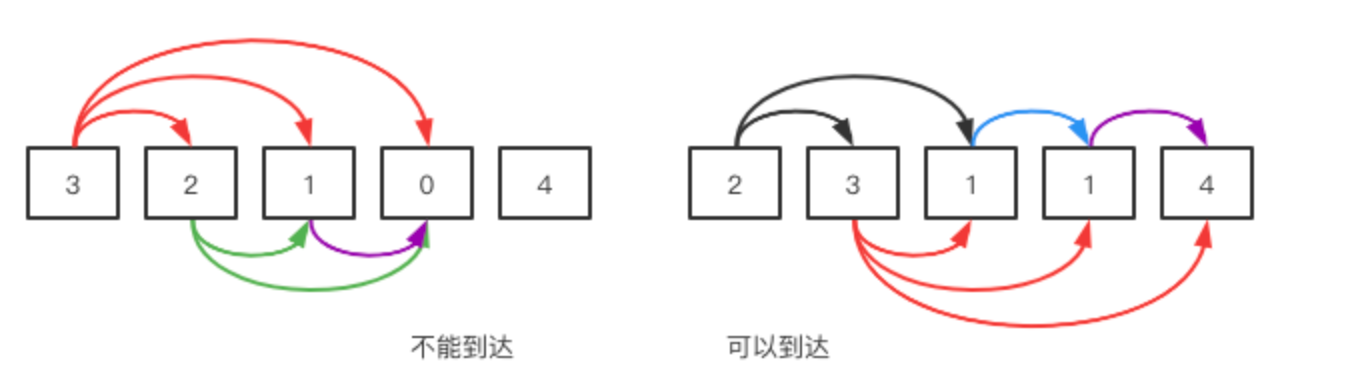
例如上面的第一个例子，3能覆盖的范围是后面的{2,1,0}，2接下来能覆盖后面的{1,0},而1只能覆盖到{0}，所以无法到达4。
而第二组序列，2能覆盖{3,1}，3可以覆盖后面的{1,1,4},已经找到一条路了。1只能到下一个1，下一个1能到4，所以这里有{2,1,1,4}和{2,3,1,1,4}两种走法，加起来有3种跳法。
我们可以定义一个cover表示最远能够到达的方位，也就是i每次移动只能在其cover的范围内移动，每移动一次，cover得到该元素数值（新的覆盖范围）的补充，让i继续移动下去。而cover每次按照下面的结果判断。如果cover大于等于了终点下标，直接return true就可以了：
cover= max(该元素数值补充后的范围, cover本身范围)
针对上图的两个序列再解释一下：
1.在第二个图中，第一个元素，nums[0]=2，此时conver=2能覆盖到{3,1}两个元素。
2.继续，第二个元素nums[1]=3，此时能继续覆盖的范围就是1+3，能覆盖{1，1，4}三个位置。此时cover=2，而”该元素数值补充后的范围“是1+3=4，所以新的conver=max{4,2}，此时就是cover>=nums.length-1。
其他情况都可以使用类似的方式来判断 ，所以代码就是：

public boolean canJump(int[] nums) {
        if (nums.length == 1) {
            return true;
        }
        //覆盖范围, 初始覆盖范围应该是0，因为下面的迭代是从下标0开始的
        int cover = 0;
        //在覆盖范围内更新最大的覆盖范围
        for (int i = 0; i <= cover; i++) {
            cover = Math.max(cover, i + nums[i]);
            if (cover >= nums.length - 1) {
                return true;
            }
        }
        return false;
}

这道题目的难点是要想到覆盖范围，而不用拘泥于每次究竟跳几步，覆盖范围是可以逐步扩展的，只有能覆盖就一定是可以跳过来的，不用管是怎么跳的。

2 最短跳跃游戏

在上题再进一步，假设一定能到达末尾，然后让你求最少到达的步数该怎么办呢？这就是LeetCode45上面的例子。可以看到，有三种走法{2,3,4}、{2,1,1,4}和{2,3,1,1,4}，那这时候该怎么办呢？
具体该怎么实现呢？网上有很多解释，代码也基本雷同，而且也很明显是将上一题的代码修改了一下，但是难在不好理解，我现在给一个比较好理解的方式：贪心+双指针。
我们重新观察一下结构图，为了便于分析，我们修改一下元素序列，我们需要四个变量：

• left用来一步步遍历数组
• steps用来记录到达当前位置的最少步数
• right表示当前步数下能够覆盖到的最大范围
• 我们还需要一个临时变量conver，假如left到达right时才更新right

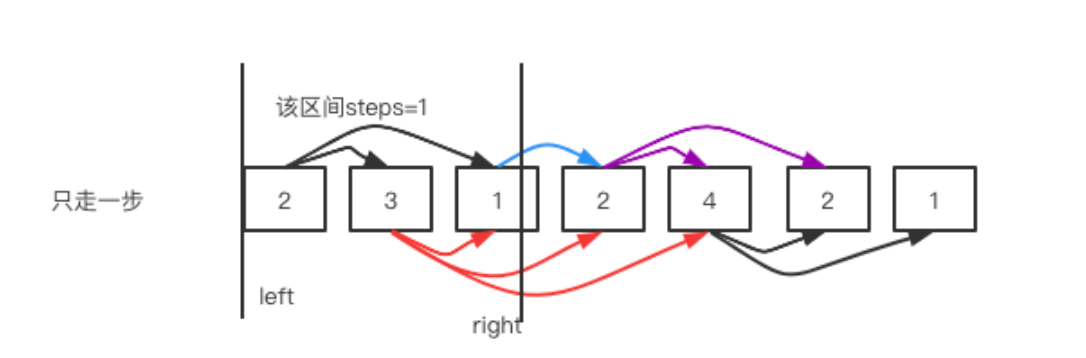在这个图中，开始的元素是 2，如果只走一步，step=1，可跳的范围是{3,1}。也就是如果只走一步，最远只能到达1，此时conver=nums[0]=2，因此我们用right=nums[2]来保存这个位置，这表示的就是走一步最远只能到nums[2]。
接下来，我们必须再走一步，step=2，如下图，此时可选元素是{3,1}， 3能让我们到达的距离是left+nums[left]=1+3=4，而1能让我们到达的位置是left+nums[left]=2+1=3，而所以我们获得最远覆盖距离conver=4 。

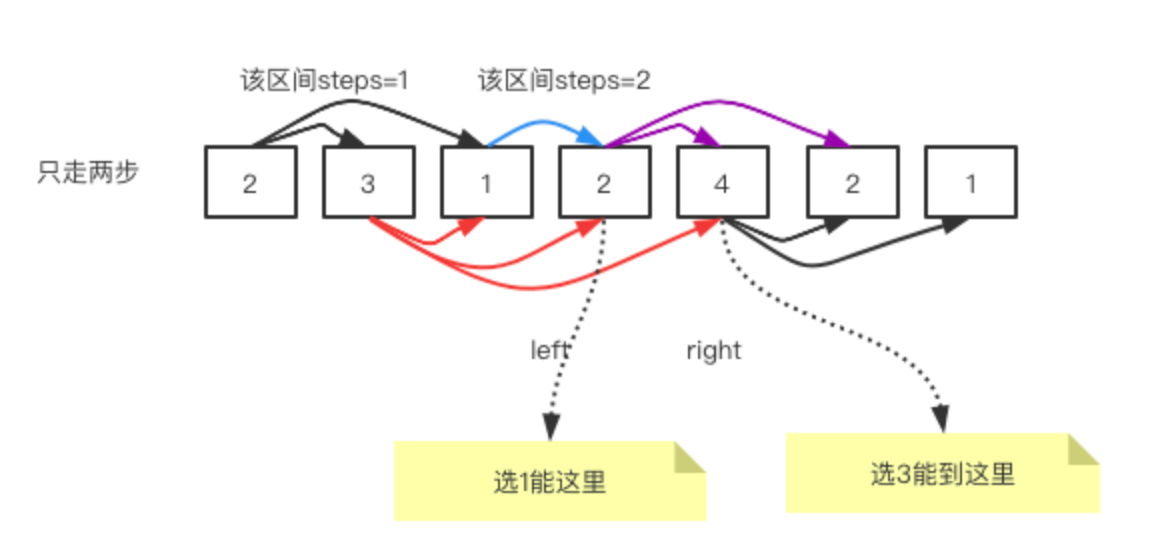然后用left和right将step=2的范围标记一下：

 此时还没有到终点，我们要继续走，在这里我们可选择的元素是{2,4}，如果选择2，则可以到达left+nums[left]=3+2=5,如果选择4则是left+nums[left]=4+4=8，已经超越边界了，所以此时一定将末尾覆盖了。

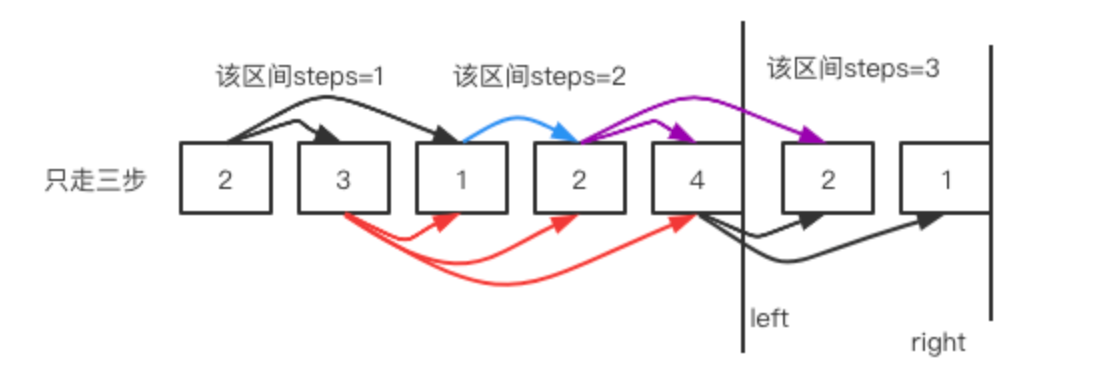
这样我们就知道最少需要走3次。
这个过程怎么用代码表示呢？看代码：

public int jump(int[] nums) {
    int right = 0;
    int maxPosition = 0;
    int steps = 0;
    for(int left=0;i<nums.length;left++){
        //找能跳的最远的
        maxPosition = Math.max(maxPosition,nums[left]+left);
        if(left==right){ //遇到边界，就更新边界，并且步数加一
            right = maxPosition;
            steps++;
        }
        //right指针到达末尾了。
        if (right >= nums.length - 1) {
            return steps;
        }
    }
    return steps;
}