程序员考公笔记之逻辑判断（图形推理）

news2024/10/6 10:32:37

文章目录

  • 写在前面
  • 1、逻辑判断
    • 1.1、图形推理
      • 1.1.1、位置类
      • 1.1.2、样式类
      • 1.1.3、数量类
      • 1.1.4、属性类
      • 1.1.5、六面体

写在前面

1、逻辑判断

1.1、图形推理

观察：先宏观，再微观

图形推理的命题形式：

  • 一组式
    观察路径：顺序看(考最多)、间隔看、分组看
  • 两组式
    观察路径：找规律、用规律（规律相同、相似？）
  • 九宫格
    观察路径：横看(优先)、竖看、S型看、O型看、米型看
  • 分组分类
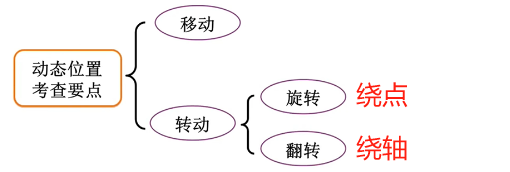
    在这里插入图片描述

1.1.1、位置类

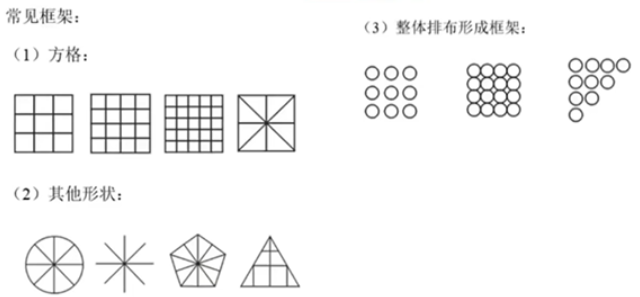
在这里插入图片描述

移动：
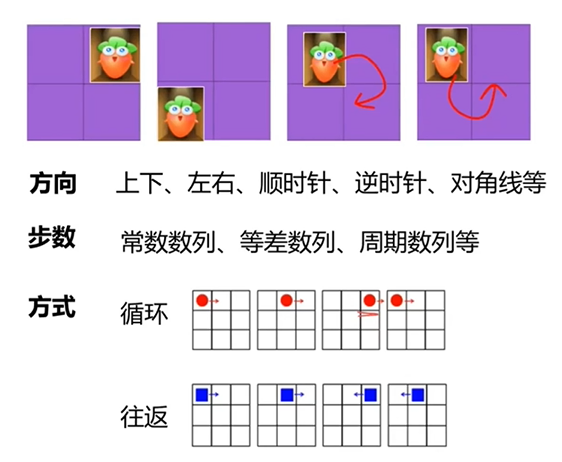
在这里插入图片描述
平移
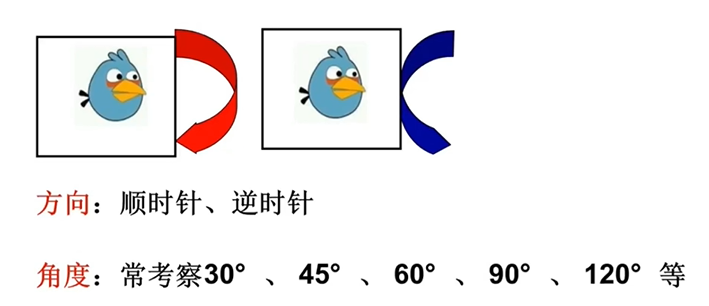
在这里插入图片描述
旋转
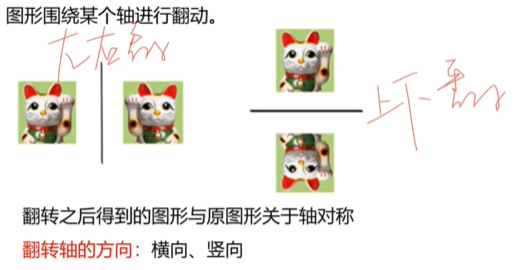
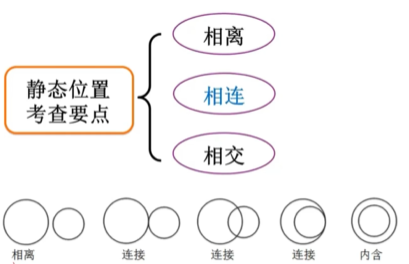
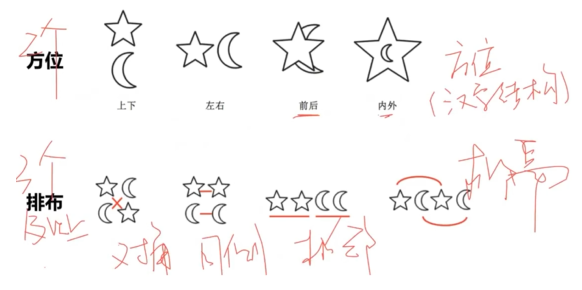
在这里插入图片描述
翻转

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

两个元素一般考虑方位，三个元素一般考虑排布
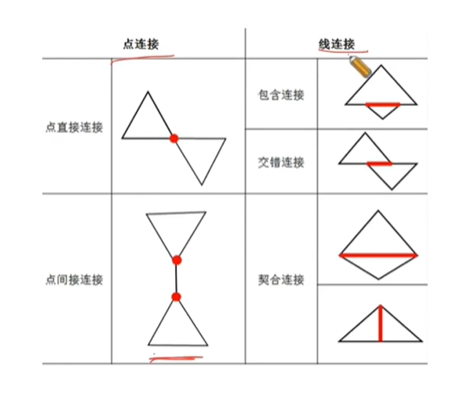
在这里插入图片描述
点连接与线连接
在这里插入图片描述
线连接要注意线连接数量，有的图形是多个线连接

相交的几种类型

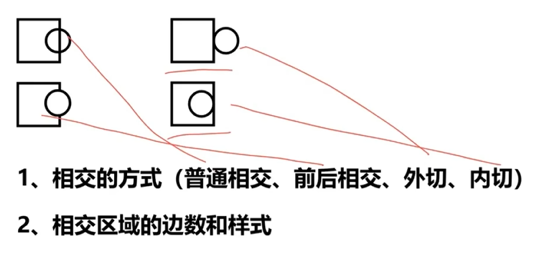
在这里插入图片描述
组成元素相似
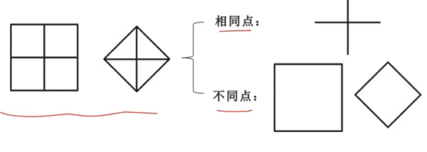
在这里插入图片描述

1.1.2、样式类

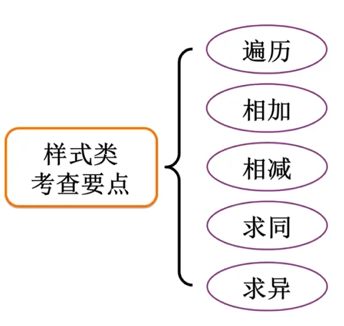
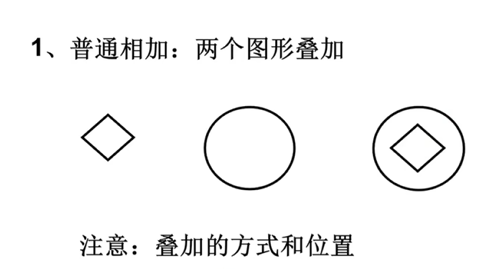
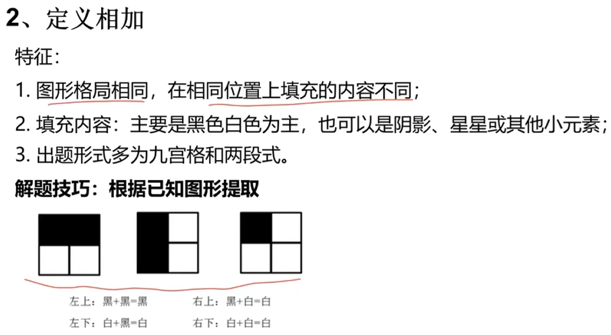
在这里插入图片描述
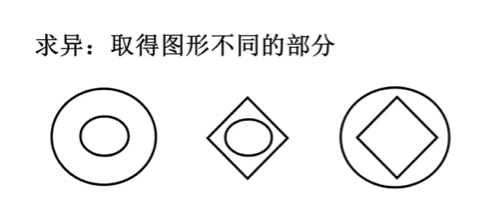
在这里插入图片描述
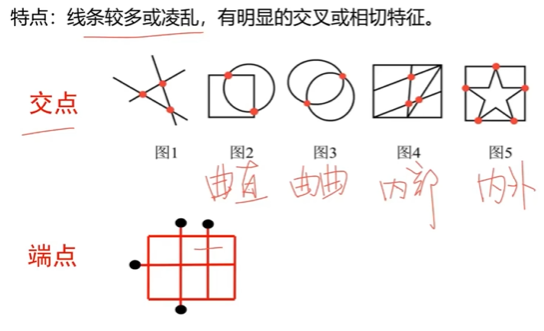
在这里插入图片描述
在这里插入图片描述
求同
在这里插入图片描述
求异
在这里插入图片描述

1.1.3、数量类

在这里插入图片描述
点
在这里插入图片描述
线
在这里插入图片描述
一笔画图形
在这里插入图片描述
奇点与笔画之间的关系

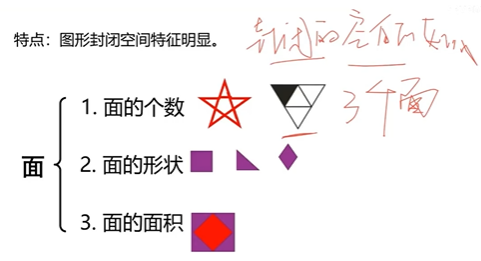
在这里插入图片描述
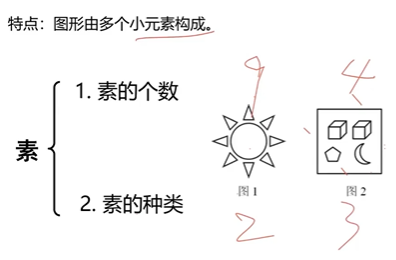
在这里插入图片描述
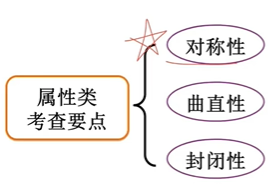
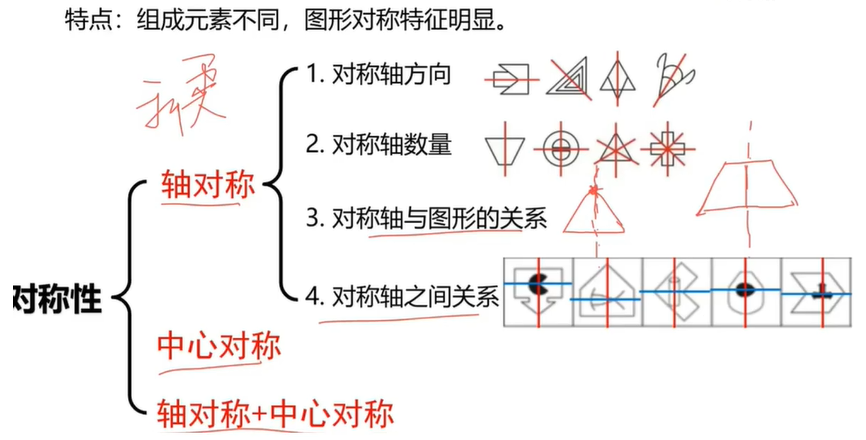
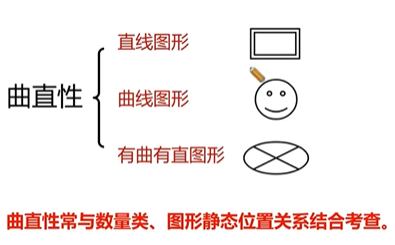
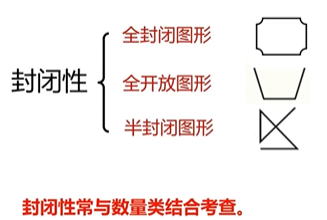
在这里插入图片描述

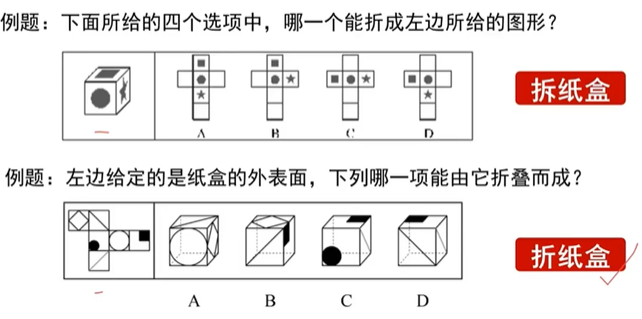
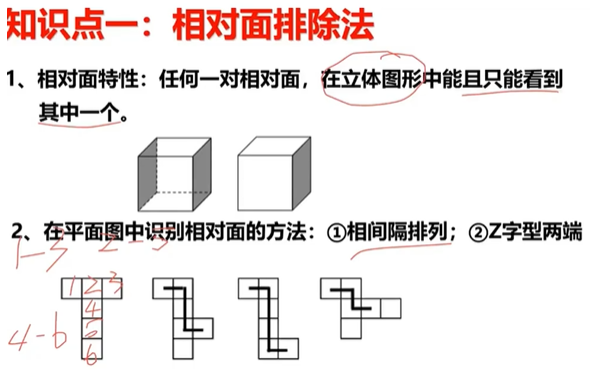
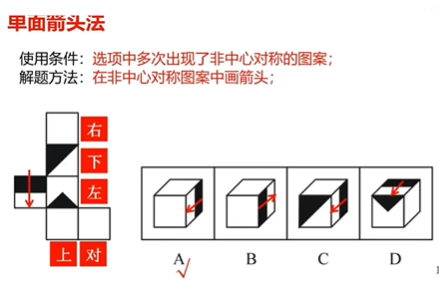
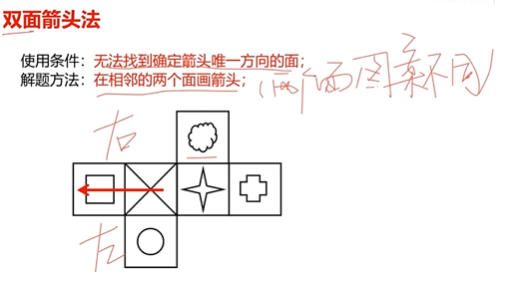
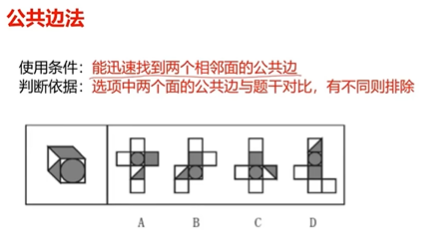
在这里插入图片描述
元素
在这里插入图片描述

1.1.4、属性类

在这里插入图片描述
在这里插入图片描述
对称性
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

1.1.5、六面体

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1302141.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

解密防泄密成功密码：银行机构案例分享迅软DSE带你走过风险之路！

解密防泄密成功密码：银行机构案例分享迅软DSE带你走过风险之路！

近日，央行发布了《中国人民银行业务领域数据安全管理办法（征求意见稿）》，旨在落实《数据安全法》有关要求，加强中国人民银行业务领域数据安全管理。 从银行业务领域来看，数据主要涉及各类市场交易数据、金…
阅读更多...
MeterSphere实战（一）

MeterSphere实战（一）

MeterSphere是一位朋友讲到的测试平台，说这东西是开源的，因为我是做测试的，很乐意了解一些新鲜事物。在我看来，测试就是要专注一些领域，然后要啥都会一点点，接着融会贯通起来，这样就可以万变不离…
阅读更多...
自定义类型详解（1）

自定义类型详解（1）

文章目录 目录1. 结构体1.1 结构的基础知识1.2 结构的声明1.3 特殊的声明1.4 结构的自引用1.5 结构体变量的定义和初始化1.6 结构体内存对齐1.7 修改默认对齐数1.8 结构体传参 2. 位段2.1 什么是位段2.2 位段的内存分配2.3 位段的跨平台问题2.4 位段的应用 3. 枚举3.1 枚举类型…
阅读更多...
vue2-elementUI部分组件样式修改

vue2-elementUI部分组件样式修改

el-radio样式： /deep/ .el-radio__input .el-radio__inner {width: 20px;height: 20px;position: relative;cursor: pointer;-webkit-appearance: none;-moz-appearance: none;appearance: none;border: 1px solid #999;border-radius: 0;outline: none;transition…
阅读更多...
亚马逊鲲鹏系统智能自动注册与AI角色养号，探索数字化新境界

亚马逊鲲鹏系统智能自动注册与AI角色养号，探索数字化新境界

在数字化时代，亚马逊鲲鹏系统以其强大的自动化功能，为用户提供了前所未有的购物体验。如果你想利用鲲鹏系统进行自动化注册，那么准备好邮箱、IP、手机号等关键信息后，你将轻松实现自动注册，为购物之旅开启智能化新篇章…
阅读更多...
V2X全方位通信部署产品支持智能交通建设！

V2X全方位通信部署产品支持智能交通建设！

来源：德思特测试测量丨德思特案例 | V2X全方位通信部署产品支持智能交通建设！ 原文链接：https://mp.weixin.qq.com/s/Fhnvcq9HA60Sed5BIGcnSw 欢迎关注虹科，为您提供最新资讯！ 01 案例背景 后疫情时代人们更注重于享…
阅读更多...
CommonJs模块化实现原理ES Module模块化原理

CommonJs模块化实现原理ES Module模块化原理

CommonJs模块化实现原理 首先看一个案例 初始化项目 npm init npm i webpack -D目录结构如下： webpack.config.js const path require("path"); module.exports {mode: "development",entry: "./src/index.js",output: {path: p…
阅读更多...
项目经理和产品经理哪个更有发展前景?

项目经理和产品经理哪个更有发展前景?

如果是单看“钱途”的话，如果是在传统行业，可能差不多；如果是在IT行业的话，可能更需要项目经理；互联网行业的话，可能更需要产品经理。 项目经理跟产品经理两个证都挺受市场欢迎的，两个岗位职责…
阅读更多...
关于粒子群算法的一些简单尝试

关于粒子群算法的一些简单尝试

粒子群算法核心思想：（鸟 粒子） （1）许多的鸟站在不同的地方； （2）每一只鸟都有自己寻找食物的初始飞行方向、飞行速度； （3）这些鸟儿每隔一段时间…
阅读更多...
高级网工在Linux服务器抓包，少不了这几条常用的tcpdump命令。

高级网工在Linux服务器抓包，少不了这几条常用的tcpdump命令。

Linux 的命令太多，tcpdump 是一个非常强大的抓包命令。有时候想看线上发生的一些问题： nginx 有没有客户端连接过来…… 客户端连接过来的时候 Post 上来的数据对不对…… 我的 Redis 实例到底是哪些业务在使用…… tcpdump 作为网络分析神器就派上用场…
阅读更多...
湖农大邀请赛shell_rce漏洞复现

湖农大邀请赛shell_rce漏洞复现

湖农大邀请赛 shell_rce 复现 在 2023 年湖南农业大学邀请赛的线上初赛中&#xff0c;有一道 shell_rce 题&#xff0c;本文将复现该题。 题目内容&#xff0c;打开即是代码&#xff1a; <?phpclass shell{public $exp;public function __destruct(){$str preg_replace…
阅读更多...
2、快速搞定Kafka术语

2、快速搞定Kafka术语

快速搞定Kafka术语 Kafka 服务端3层消息架构 Kafka 客户端Broker 如何持久化数据小结 Kafka 服务端 3层消息架构 第 1 层是主题层&#xff0c;每个主题可以配置 M 个分区&#xff0c;而每个分区又可以配置 N 个副本。第 2 层是分区层&#xff0c;每个分区的 N 个副本中只能有…
阅读更多...
Java集合进阶

Java集合进阶

目录 集合体系结构 Collection集合 List集合 ArrayList集合 LinkedList集合 集合体系结构 注意:有序:存进去的数组和取出来时一样 而不是大小的那种有序 Collection集合 单列集合顶层接口Collection import java.util.ArrayList; import java.util.Collection;public cl…
阅读更多...
模块化机房在大数据时代的角色：高效、可扩展的数据存储和处理平台

模块化机房在大数据时代的角色：高效、可扩展的数据存储和处理平台

随着大数据时代的到来&#xff0c;数据已经成为企业竞争的核心资源。然而&#xff0c;传统的数据中心已经无法满足现代业务的需求&#xff0c;尤其是在数据存储和处理方面。模块化机房作为一种新型的数据中心建设模式&#xff0c;具有高效、可扩展等优势&#xff0c;逐渐成为大…
阅读更多...
SQL命令---删除字段

SQL命令---删除字段

介绍 使用sql语句删除表字段。 命令 alter table 表名 drop 字段名;例子 删除a表中的name字段。 alter table a drop name;下面是执行删除后的表结构&#xff1a;
阅读更多...
《opencv实用探索·十六》opencv直方图计算calcHist函数解析

《opencv实用探索·十六》opencv直方图计算calcHist函数解析

直方图理解&#xff1a; &#xff08;对于8位灰度图像亮度/灰度为(0-255)&#xff0c;12位灰度图像亮度/灰度为(0-4095)&#xff09; 以8位图像为例&#xff0c;亮度分为0到255共256个数值&#xff0c;数值越大&#xff0c;代表的亮度越高。其中0代表纯黑色的最暗区域&#xff…
阅读更多...
XCube——用于超高分辨率 3D 形状和场景的生成模型！

XCube——用于超高分辨率 3D 形状和场景的生成模型！

他们的方法在稀疏体素网格的层次结构上训练潜在扩散模型的层次结构。他们在稀疏结构 VAE 的潜在空间上进行扩散&#xff0c;它为层次结构的每个级别学习紧凑的潜在表示。 XCube 是稀疏体素层次上的分层潜在扩散模型&#xff0c;即从粗到细的 3D 稀疏体素网格序列&#xff0c;使…
阅读更多...
OpenWRT搭建本地web站点并结合内网穿透实现公网远程访问

OpenWRT搭建本地web站点并结合内网穿透实现公网远程访问

文章目录 前言1. 检查uhttpd安装2. 部署web站点3. 安装cpolar内网穿透4. 配置远程访问地址5. 配置固定远程地址 前言 uhttpd 是 OpenWrt/LuCI 开发者从零开始编写的 Web 服务器&#xff0c;目的是成为优秀稳定的、适合嵌入式设备的轻量级任务的 HTTP 服务器&#xff0c;并且和…
阅读更多...
【高数：3 无穷小与无穷大】

【高数：3 无穷小与无穷大】

【高数&#xff1a;3 无穷小与无穷大】 1 无穷小与无穷大2 极限运算法则3 极限存在原则4 趋于无穷小的比较 参考书籍&#xff1a;毕文斌, 毛悦悦. Python漫游数学王国[M]. 北京&#xff1a;清华大学出版社&#xff0c;2022. 1 无穷小与无穷大 无穷大在sympy中用两个字母o表示无…
阅读更多...
数据结构--二叉树

数据结构--二叉树

目录 1.二叉树链式结构的实现 1.1 前置说明 1.2 二叉树的遍历 1.2.1 前序、中序以及后序遍历 1.2.2 层序遍历及判断是否为完全二叉树 1.3 节点个数&#xff0c;叶子节点个数&#xff0c;第k层节点个数以及高度等 1.4 二叉树的创建和销毁 1.二叉树链式结构的实现 1.1 前置说…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023