粒子群算法核心思想:(鸟 = 粒子)
(1)许多的鸟站在不同的地方;
(2)每一只鸟都有自己寻找食物的初始飞行方向、飞行速度;
(3)这些鸟儿每隔一段时间寻找一次食物,通过搜集所有鸟的信息,来寻找食物最充足的地方;
一、以公式原理的实现过程逐步讲解;
1、初始化N个粒子,这些粒子有着随机的初始位置和随机的初始速度;
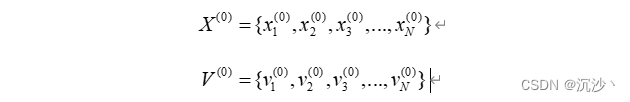
2、计算这些粒子下一步位置,所有的粒子均朝着随机方向以随机的速度移动;
![]()
3、寻找所有粒子中的最小值,以及寻找每个粒子在不同时刻的最小值;
先寻找所有粒子中的最小值,对所有的粒子求最小值;
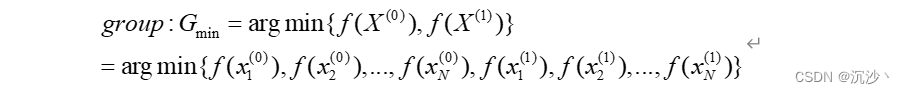
然后选在每个粒子在不同时刻的最小值;每个粒子自身的最小值是能够决定下一步该粒子移动方向和速度的量;

4、更新粒子搜寻的速度,并且更新粒子搜寻的方向,这里不仅有速度的大小,还有方向的角度,因此是一个矢量;
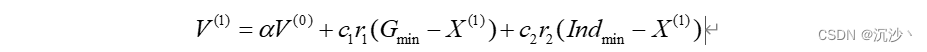
这个里面,随机优化的核心是其初始位置和速度的随机性。因此,更新后的速度应一定程度尽可能保持其先前的速度,以保持其随机性;这个α是惯性权重系数,建议为[0.5,0.8]。
![]()
我们还应该在这次迭代中调整速度以接近组最小值,因为它至少是这一步中最好的一个;这个里面c1是权重系数,r1是随机权重系数,第一个c1代表全局最小的权重,推荐范围 0.1-2 ,r1是为了提高随机性,推荐范围 0-1;
![]()
另一个同理,c2是代表局部最优的权重,推荐范围 [0.1~2],r2是随机权重系数,推荐范围 0-1;
![]()
5、设计停止条件
重复迭代并在特定位置停止:
(1)达到最大迭代次数k;
(2)变化的目标函数小于预设阈值ε;
(3)我们经常设置速度和位置的限制,以避免不稳定和大的振荡

二、以代码进行逐步讲解
最后通过代码进行实现:求取函数最小值

第一步:首先初始化;
1、定义粒子群个数;N = 100; %群体粒子个数
2、定义粒子维数;几个变量几维度;D = 2;
3、定义权重因子大小;c1 =2;c2 =2;
4、定义速度范围;这个Vmax = 1; Vmin = -1;
5、定义位置范围;(变量的范围)(这里这么写是因为xy的范围不一致,就分开给出范围)
X1max =1;
X1min =-1;
X2max =3;
X2min =-2;
Xmax = [X1max X2max];
Xmin = [X1min X2min];
第二步:然后定义初始随机量:
1、定义初始随机位置;
x1 = rand(N,1) * (X1max-X1min)+X1min;
x2 = rand(N,1) * (X2max-X2min)+X2min;
2、定义初始随机速度;
v = rand(N,D) * (Vmax-Vmin)+Vmin;
第三步:初始化个体最优位置和最优值
p=x;
pbest = ones(N,1); %% 创建一个数组,用于存储每个粒子对应的适应度函数值
for i = 1:N
pbest(i) = func2(x(i,:)); % 求出初始化种群对应的目标函数值
end
第四步:初始化全局最优位置和最优值;
g = ones(1,D);
gbest = inf;
for i = 1:N
if(pbest(i) < gbest)
g = p(i,:);
gbest = pbest(i);
end
end
第五步:粒子群群体寻优;这里就不列了,直接把所有代码给出来;这里是大头;
%%%%%%%%%%%%%%粒子群算法求函数极值%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%
function counti()
clear all; %清除所有变量
% close all; %清图
clc; %清屏
N = 100; %群体粒子个数
D = 2; %粒子维数 变量的个数
T = 1000; %最大迭代次数
c1 =2; %权重因子 c1 [0.1 - 2] 越大,保持原来速度的能力越强
c2 =2; %权重因子 c2 [0.1 - 2]
Wmax = 0.8; %惯性权重最大值
Wmin = 0.4; %惯性权重最小值
X1max =1; %位置最大值
X1min =-1; %位置最小值
X2max =3; %位置最大值
X2min =-2; %位置最小值
Xmax = [X1max X2max];
Xmin = [X1min X2min];
Vmax = 1; %速度最大值
Vmin = -1; %速度最小值
%%%%%%%%%%%%初始化种群个体(限定位置和速度)%%%%%%%%%%%%
x1 = rand(N,1) * (X1max-X1min)+X1min;
x2 = rand(N,1) * (X2max-X2min)+X2min;
x = [x1 x2];
v = rand(N,D) * (Vmax-Vmin)+Vmin;
%%%%%%%%%%%%%初始化个体最优位置和最优值%%%%%%%%%%%%%
p = x;
pbest = ones(N,1); %% 创建一个数组,用于存储每个粒子对应的适应度函数值
for i = 1:N
pbest(i) = func2(x(i,:)); % 求出初始化种群对应的目标函数值
end
%%%%%%%%%%%%%初始化全局最优位置和最优值%%%%%%%%%%%%
g = ones(1,D); % 创建一个数组和变量用于保存最优变量和目标函数
gbest = inf; %inf 无穷大
for i = 1:N % 这一步当中找到种群最优目标函数值
if(pbest(i) < gbest)
g = p(i,:);
gbest = pbest(i);
end
end
gb = ones(1,T); % 建立此项用于保存种群中每一代中的的最优值
%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%
for i = 1:T
for j = 1:N
%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%
if (func2(x(j,:)) < pbest(j)) % 新的个体是否小于原来的个体,如果小于则保存新的个体
p(j,:) = x(j,:);
pbest(j) = func2(x(j,:));
end
%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%%%%
if(pbest(j) < gbest)
g = p(j,:);
gbest = pbest(j);
end
%%%%%%%%%%%计算动态惯性权重值%%%%%%%%%%%%%%%
w = Wmax-(Wmax-Wmin)*i/T;
%%%%%%%%%%%%更新位置和速度值%%%%%%%%%%%%%%%
v(j,:) = w*v(j,:)+c1*rand*(p(j,:)-x(j,:))...
+c2*rand*(g-x(j,:)); %计算对应的速度公式
x(j,:) = x(j,:)+v(j,:); %更新粒子群当中对应的基因
%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%
% 检查单个粒子的速度和位置信息是否超过当前最大限制
for ii = 1:D % 如果超过的话就在原来的范围内重新生成个体
if (v(j,ii) > Vmax) || (v(j,ii) < Vmin)
v(j,ii) = rand * (Vmax-Vmin)+Vmin;
end
if (x(j,ii) > Xmax(ii)) || (x(j,ii) < Xmin(ii))
x(j,ii) = rand * (Xmax(ii)-Xmin(ii))+Xmin(ii);
end
end
end
%%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%%%
gb(i) = gbest;
end
g; %最优个体
gb(end); %最优值
figure(1)
plot(gb)
hold on
grid on
xlabel('迭代次数');
ylabel('适应度值');
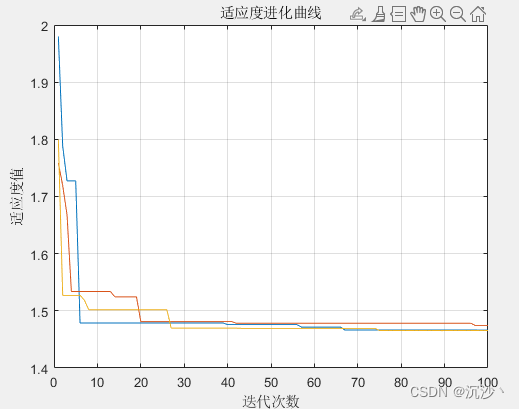
title('适应度进化曲线')
hold on
end
%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%
function value = func2(x)
value = (3*cos(x(1)*x(2))+x(1)+x(2)^2);
end %这里是适应度函数,也可以在同一文件夹下独立建立函数,也可以直接写在后面。
最终仿真结果: