直方图理解：
（对于8位灰度图像亮度/灰度为(0-255)，12位灰度图像亮度/灰度为(0-4095)）
以8位图像为例，亮度分为0到255共256个数值，数值越大，代表的亮度越高。其中0代表纯黑色的最暗区域，255表示最亮的纯白色。亮度分为了5个区域，分别是黑色，阴影，中间调，高光和白色。直方图用来统计一幅图像某个亮度像素数量。

直方图函数解析：

void calcHist( const Mat* images, int nimages,
               const int* channels, InputArray mask,
               OutputArray hist, int dims, const int* histSize,
               const float** ranges, bool uniform=true, bool accumulate=false );

images：输入的图像的指针，可以是多幅图像，所有的图像必须有同样的深度（CV_8U or CV_32F）。同时一副图像可以有多个channes。
nimages：输入图像的个数
channels：需要统计直方图的第几通道。用来计算直方图的channes的数组。比如输入是2副图像，第一副图像有0，1，2共三个channel，第二幅图像只有0一个channel，那么输入就一共有4个channes，如果int channels[3] = {3, 2, 0}，那么就表示是使用第二副图像的第一个通道和第一副图像的第2和第0个通道来计算直方图。
mask：掩膜，如果是空矩阵则表示图像中所有位置的像素都计入直方图中，如果mask不为空，那么它必须是一个8位（CV_8U）的数组，并且与输入图像尺寸相同，找到mask非0像素区域，把这些区域对应到输入图像区域，然后把这些区域参与直方图计算。
hist:输出的直方图数组
dims：需要统计直方图通道的个数，通常为1
histSize：指的是直方图分成多少个区间，就是 bin的个数。
const float** ranges： 统计像素值得区间。
uniform=true::是否对得到的直方图数组进行归一化处理
accumulate=false：在多个图像时，是否累计计算像素值得个数

几个例子理解直方图参数含义：
首先我们对一个mat图像做几个设定如下：
（1）8位单通道灰度图，那么这个图像灰度范围为0-255
（2）mat图像总像素个数为10000
（3）灰度范围在0-127时像素个数为8000， 灰度范围128-255时像素个数为2000
（3）灰度范围在0-84时像素个数为3000， 灰度范围85-170时像素个数为6000，灰度范围171-255时像素个数为1000

int main()
{
	Mat mat = cv::imread("1.tif", -1);

	int max_value = 0;
	int channels[] = { 0 };
	const int histSize[] = { 256 };

	float range[] = { 0, 256};
	const float* ranges[] = { range };

	cv::Mat hist;
	cv::calcHist(&mat, 1, channels, cv::Mat(), hist, 1, histSize, ranges, true, false);

	int sum = 0;
	for (int i = 0; i < 255; i++)
	{
		sum += hist.at<float>(i);
	}
	return 0;
}

上面代码中可知像素值范围range为0-255（不包含256），histSize为256相当于把rang(0-255)分为256份。for循环对histSize总份数进行遍历，相当于遍历0-255每个灰度，这样可以拿到每个灰度下的像素个数，最终sum总和等于10000。

int main()
{
	Mat mat = cv::imread("1.tif", -1);

	int max_value = 0;
	int channels[] = { 0 };
	const int histSize[] = { 2 };

	float range[] = { 0, 256};
	const float* ranges[] = { range };

	cv::Mat hist;
	cv::calcHist(&mat, 1, channels, cv::Mat(), hist, 1, histSize, ranges, true, false);

	int sum = 0;
	for (int i = 0; i < 2; i++)
	{
		sum += hist.at<float>(i);
	}
	return 0;
}

上面代码中range灰度范围为0-255，histSize把灰度范围分为两份，第一份灰度范围0-127，第二份灰度范围128-255
for循环中遍历总份数，即遍历两份，第一份可以拿到灰度范围0-127的所有像素之和，即8000，第二份可以拿到128-255范围所有像素之和，即2000

int main()
{
	Mat mat = cv::imread("1.tif", -1);

	int max_value = 0;
	int channels[] = { 0 };
	const int histSize[] = { 3 };

	float range[] = { 0, 256};
	const float* ranges[] = { range };

	cv::Mat hist;
	cv::calcHist(&mat, 1, channels, cv::Mat(), hist, 1, histSize, ranges, true, false);

	int sum = 0;
	for (int i = 0; i < 3; i++)
	{
		sum += hist.at<float>(i);
	}
	return 0;
}

上面代码中range范围0-255，histSize把range总共分为三份，即0-84，85-170，171-255
for循环遍历histSize，在第一份中可以拿到灰度范围在0-84的总像素个数，即3000，在第二份中可以拿到灰度范围在85-170的总像素个数，即6000，第三份可以拿到171-255范围的总像素个数，即1000

下面是直方图的一个具体应用，8位三通道计算直方图案例：

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;

int main() {
    // 读取图像
    Mat image = imread("your_image.jpg");

    if (image.empty()) {
        cerr << "Error: Could not read the image." << endl;
        return -1;
    }

    // 设置直方图参数
    int histSize = 256;  // 直方图的 bin 数量
    float range[] = {0, 256};  // 像素值范围
    const float* histRange = {range};
    bool uniform = true;  // 直方图是否均匀
    bool accumulate = false;  // 是否累积直方图

    // 计算蓝色通道的直方图
    int channelB = 0;  // 蓝色通道索引
    Mat histB;
    calcHist(&image, 1, &channelB, Mat(), histB, 1, &histSize, &histRange, uniform, accumulate);

    // 计算绿色通道的直方图
    int channelG = 1;  // 绿色通道索引
    Mat histG;
    calcHist(&image, 1, &channelG, Mat(), histG, 1, &histSize, &histRange, uniform, accumulate);

    // 计算红色通道的直方图
    int channelR = 2;  // 红色通道索引
    Mat histR;
    calcHist(&image, 1, &channelR, Mat(), histR, 1, &histSize, &histRange, uniform, accumulate);

    // 绘制直方图
    int histWidth = 512;
    int histHeight = 400;
    int binWidth = cvRound((double) histWidth / histSize);

    Mat histImage(histHeight, histWidth, CV_8UC3, Scalar(0, 0, 0));

    // 归一化直方图数据
    normalize(histB, histB, 0, histImage.rows, NORM_MINMAX, -1, Mat());
    normalize(histG, histG, 0, histImage.rows, NORM_MINMAX, -1, Mat());
    normalize(histR, histR, 0, histImage.rows, NORM_MINMAX, -1, Mat());

    // 绘制直方图
     for (int i = 1; i < histSize; ++i) {
        line(histImage, Point(binWidth * (i - 1), cvRound(histB.at<float>(i - 1))),
            Point(binWidth * (i), cvRound(histB.at<float>(i))),
            Scalar(255, 0, 0), 2, 8, 0);
        line(histImage, Point(binWidth * (i - 1), cvRound(histG.at<float>(i - 1))),
            Point(binWidth * (i), cvRound(histG.at<float>(i))),
            Scalar(0, 255, 0), 2, 8, 0);
        line(histImage, Point(binWidth * (i - 1),cvRound(histR.at<float>(i - 1))),
            Point(binWidth * (i), cvRound(histR.at<float>(i))),
            Scalar(0, 0, 255), 2, 8, 0);
    }

    // 显示原始图像和直方图
    imshow("Original Image", image);
    imshow("Histogram", histImage);

    waitKey(0);
    return 0;
}

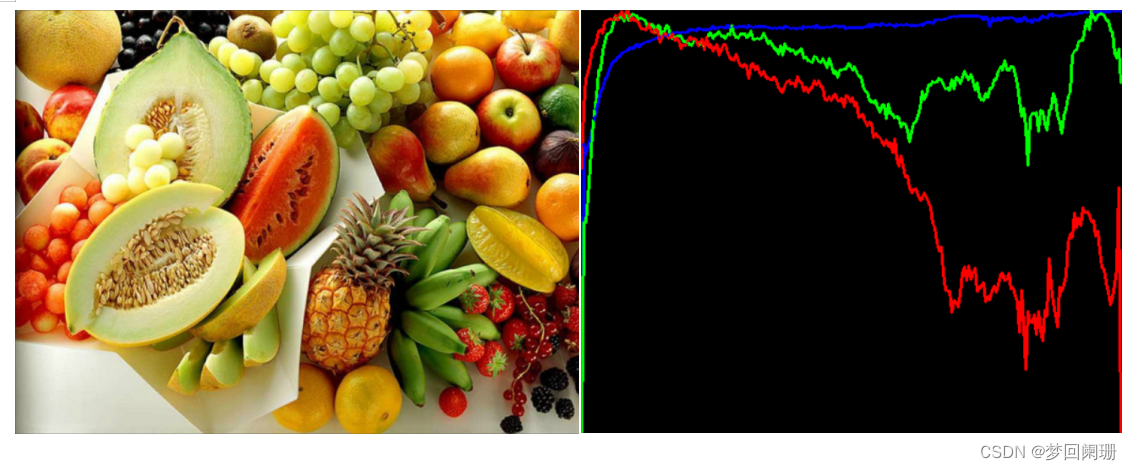
也可也遍历拿到BGR每个通道下0-255每个灰度的像素个数
比如遍历B通道

for(int i = 0; i < 256; i++)
{
	float count = cvRound(histB.at<float>(i - 1);
}

0-256为每个灰度，for循环遍历每个灰度，并拿到该灰度下像素的个数，比如i=100，count=20表示，灰度为100的像素有20个。