文章目录
- 目录
- 1. 结构体
- 1.1 结构的基础知识
- 1.2 结构的声明
- 1.3 特殊的声明
- 1.4 结构的自引用
- 1.5 结构体变量的定义和初始化
- 1.6 结构体内存对齐
- 1.7 修改默认对齐数
- 1.8 结构体传参
- 2. 位段
- 2.1 什么是位段
- 2.2 位段的内存分配
- 2.3 位段的跨平台问题
- 2.4 位段的应用
- 3. 枚举
- 3.1 枚举类型的定义
- 3.2 枚举的优点
- 3.3 枚举的使用
- 4. 联合(共用体)
- 4.1 联合类型的定义
- 4.2 联合的特点
- 4.3 联合大小的计算
目录
- 结构体
- 位段
- 枚举
- 联合体
- 通讯录的实现
1. 结构体
1.1 结构的基础知识
结构是一些值的集合,这些值称为成员变量,结构的每个成员可以是不同类型的变量。
区分:
数组:一组相同类型元素的集合
1.2 结构的声明

举个例子:

1.3 特殊的声明
在声明结构的时候,可以不完全的声明。
struct
{
int a;
char c;
float f;
}x;
struct
{
int a;
char c;
float f;
}* p;
//上面的两个结构在声明的时候省略掉了结构体标签(tag)。
int main()
{
//p = &x;//err
return 0;
}
注:
编译器会把上面的两个声明当成完全不同的两个类型,所以是非法的。
1.4 结构的自引用
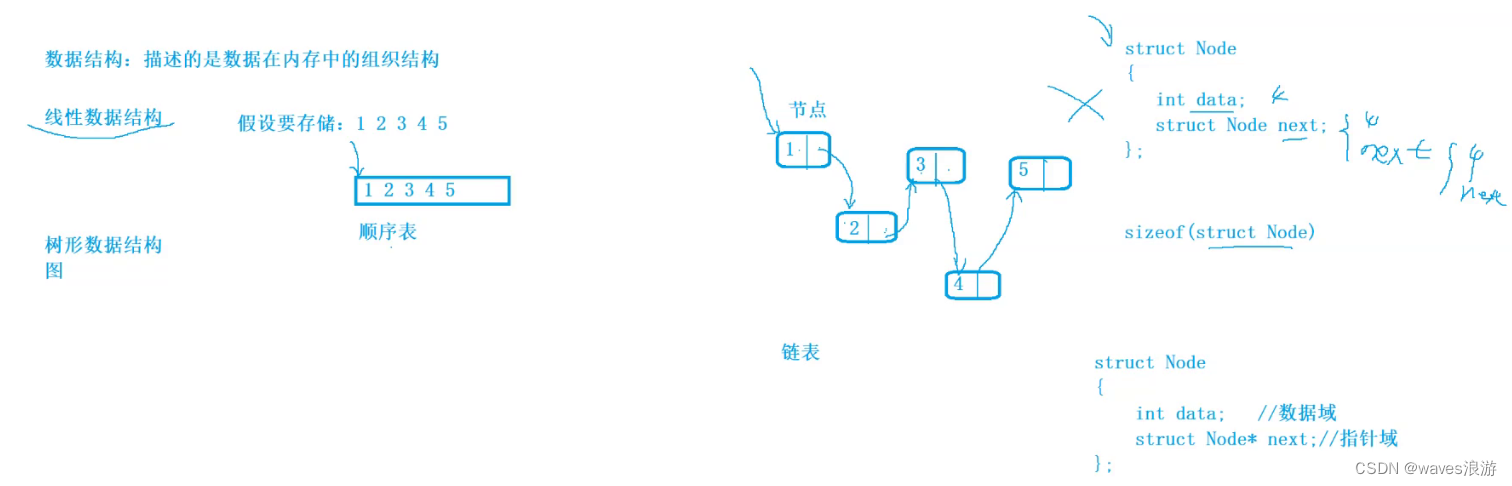
以下写法是错误的:
typedef struct
{
int data;
Node* next;
}Node;
应该这样写:
typedef struct Node
{
int data;
struct Node* next;
}Node;
int main()
{
Node n = { 0 };
return 0;
}
1.5 结构体变量的定义和初始化
#include <stdio.h>
struct SN
{
char c;
int i;
}sn1 = { 'q', 100 }, sn2 = { .i = 200, .c = 'w'};//全局变量
struct S
{
double d;
struct SN sn;
int arr[10];
};
int main()
{
struct SN sn3, sn4;//局部变量
printf("%c %d\n", sn2.c, sn2.i);
struct S s = { 3.14, { 'a', 99 }, { 1, 2, 3 } };
printf("%lf %c %d\n", s.d, s.sn.c, s.sn.i);
int i = 0;
for (i = 0; i < 10; i++)
{
printf("%d ", s.arr[i]);
}
return 0;
}
1.6 结构体内存对齐
结构体的对齐规则:
- 第一个成员在与结构体变量偏移量为0的地址处。
- 其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。
对齐数 = 编译器默认的一个对齐数与该成员大小的较小值。
- VS中默认的值为8
- Linux中没有默认对齐数,对齐数就是成员自身的大小
- 结构体总大小为最大对齐数(每个成员变量都有一个对齐数)的整数倍。
- 如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍。
我们可以通过代码来观察:
#include <stdio.h>
#include <stddef.h>
struct S1
{
char c1;
int i;
char c2;
};
struct S2
{
int i;
char c1;
char c2;
};
int main()
{
printf("%d\n", sizeof(struct S1));//12
printf("%d\n", sizeof(struct S2));//8
//可以计算结构体成员相较于结构体起始位置的偏移量
printf("%d\n", offsetof(struct S1, c1));//0
printf("%d\n", offsetof(struct S1, i));//4
printf("%d\n", offsetof(struct S1, c2));//8
return 0;
}
再举个例子:
#include <stdio.h>
struct S3
{
double d;
char c;
int i;
};
struct S4
{
char c1;
struct S3 s3;
double d;
};
int main()
{
printf("%d\n", sizeof(struct S3));//16
printf("%d\n", sizeof(struct S4));//32
return 0;
}
如果结构体中有数组,我们将它看作一个一个的元素即可:
#include <stdio.h>
#include <stddef.h>
struct S
{
char c;
int arr[4];
};
int main()
{
printf("%d\n", offsetof(struct S, arr[0]));//4
printf("%d\n", offsetof(struct S, arr[1]));//8
printf("%d\n", offsetof(struct S, arr[2]));//12
printf("%d\n", offsetof(struct S, arr[3]));//16
printf("%d\n", sizeof(struct S));//20
return 0;
}
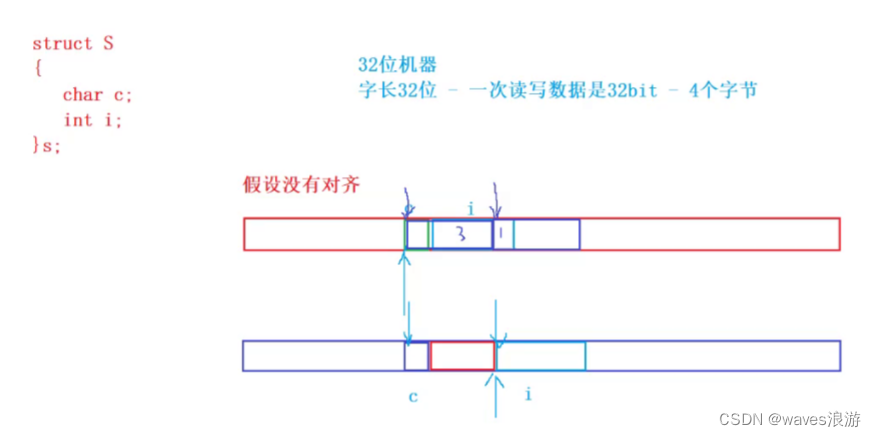
为什么存在内存对齐?
- 平台原因(移植原因):
不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。- 性能原因:
数据结构(尤其是栈)应该尽可能地在自然边界上对齐。原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访问。
总体来说:
结构体的内存对齐是拿空间来换取时间的做法。
那在设计结构体的时候,我们既要满足对齐,又要节省空间,如何做到:
让占用空间小的成员尽量集中在一起。
#include <stdio.h>
struct S1
{
char c1;
int i;
char c2;
};
struct S2
{
int i;
char c1;
char c2;
};
int main()
{
printf("%d\n", sizeof(struct S1));//12
printf("%d\n", sizeof(struct S2));//8
return 0;
}
S1和S2类型的成员一模一样,但是S1和S2所占空间的大小有了一些区别。
1.7 修改默认对齐数
之前我们见过了 #pragma 这个预处理指令,这里我们再次使用,可以改变我们的默认对齐数。
#include <stdio.h>
#pragma pack(8)//设置默认对齐数为8
struct S1
{
char c1;
int i;
char c2;
};
#pragma pack()//取消设置的默认对齐数,还原为默认
#pragma pack(1)//设置默认对齐数为1
struct S2
{
char c1;
int i;
char c2;
};
#pragma pack()//取消设置的默认对齐数,还原为默认
int main()
{
printf("%d\n", sizeof(struct S1));//12
printf("%d\n", sizeof(struct S2));//6
return 0;
}
结论:
结构在对齐方式不合适的时候,我们可以自己更改默认对齐数。
一道笔试题:
写一个宏,计算结构体中某变量相对于首地址的偏移,并给出说明
考察: offsetof 宏的实现
注:这里还没学习宏,可以放在宏讲解完后再实现。
1.8 结构体传参
#include <stdio.h>
struct S
{
int data[100];
int num;
};
void print1(struct S tmp)
{
printf("%d\n", tmp.num);
}
void print2(const struct S* ps)
{
printf("%d\n", ps->num);
}
int main()
{
struct S s = { { 1, 2, 3 }, 100 };
print1(s);
print2(&s);
return 0;
}
上面的 print1 和 print2 函数哪个好些?
答案是:首选print2函数。
原因:
函数传参的时候,参数是需要压栈,会有时间和空间上的系统开销。
如果传递一个结构体对象的时候,结构体过大,参数压栈的的系统开销比较大,所以会导致性能的下降。
结论:
结构体传参的时候,要传结构体的地址。
2. 位段
结构体讲完就得讲讲结构体实现位段的能力。
2.1 什么是位段
位段的声明和结构是类似的,有两个不同:
- 位段的成员必须是 char、int、unsigned int 或 signed int 。
- 位段的成员名后边有一个冒号和一个数字。
#include <stdio.h>
//00
//01
//10
//11
//比如_a只有这四种取值,那么只需要两个比特位就可以解决,就不需要一个整型那么大的空间了
struct A
{
int _a : 2;//二进制位
int _b : 5;
int _c : 10;
int _d : 30;
};
int main()
{
printf("%d\n", sizeof(struct A));//8
return 0;
}
2.2 位段的内存分配
- 位段的成员可以是 int、unsigned int、signed int 或者是 char (属于整形家族)类型
- 位段的空间上是按照需要以4个字节( int )或者1个字节( char )的方式来开辟的。
- 位段涉及很多不确定因素,位段是不跨平台的,注重可移植的程序应该避免使用位段。
我们来看一下在VS上位段的内存分配:
#include <stdio.h>
struct S
{
char a : 3;
char b : 4;
char c : 5;
char d : 4;
};
int main()
{
struct S s = { 0 };
s.a = 10;
s.b = 12;
s.c = 3;
s.d = 4;
printf("%d\n", sizeof(s));//3
return 0;
}


2.3 位段的跨平台问题
- int 位段被当成有符号数还是无符号数是不确定的。
- 位段中最大位的数目不能确定。(16位机器最大16,32位机器最大32,写成27,在16位机器会出问题。)
- 位段中的成员在内存中从左向右分配,还是从右向左分配标准尚未定义。
- 当一个结构包含两个位段,第二个位段成员比较大,无法容纳于第一个位段剩余的位时,是舍弃剩余的位还是利用,这是不确定的。
总结: 跟结构相比,位段可以达到同样的效果,并且可以很好的节省空间,但是有跨平台的问题存在。
2.4 位段的应用
IP数据包的格式:
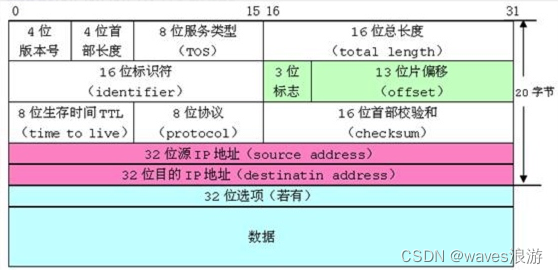
3. 枚举
枚举顾名思义就是一一列举,把可能的取值一一列举。
比如我们现实生活中:
一周的星期一到星期日是有限的7天,可以一一列举。
性别有:男、女、保密,也可以一一列举。
月份有12个月,也可以一一列举
这里就可以使用枚举了。
3.1 枚举类型的定义
#include <stdio.h>
enum Color
{
RED,
GREEN,
BLUE
};
int main()
{
printf("%d\n", RED);//0
printf("%d\n", GREEN);//1
printf("%d\n", BLUE);//2
return 0;
}
{}中的内容是枚举类型的可能取值,也叫枚举常量。
这些可能取值都是有值的,默认从0开始,依次递增1,当然在声明枚举类型的时候也可以赋初值。
例如:
#include <stdio.h>
enum Color
{
RED = 4,
GREEN,
BLUE
};
int main()
{
printf("%d\n", RED);//4
printf("%d\n", GREEN);//5
printf("%d\n", BLUE);//6
return 0;
}
#include <stdio.h>
enum Color
{
RED,
GREEN = 8,
BLUE
};
int main()
{
printf("%d\n", RED);//0
printf("%d\n", GREEN);//8
printf("%d\n", BLUE);//9
return 0;
}
#include <stdio.h>
enum Color
{
RED = 4,
GREEN = 8,
BLUE = 1
};
int main()
{
printf("%d\n", RED);//4
printf("%d\n", GREEN);//8
printf("%d\n", BLUE);//1
return 0;
}
3.2 枚举的优点
我们可以使用 #define 定义常量,为什么非要使用枚举?
枚举的优点:
- 增加代码的可读性和可维护性
- 和#define定义的标识符比较枚举有类型检查,更加严谨。
- 便于调试
- 使用方便,一次可以定义多个常量
3.3 枚举的使用
enum Color
{
RED,
GREEN,
BLUE
};
int main()
{
enum Color c = GREEN;
return 0;
}
4. 联合(共用体)
4.1 联合类型的定义
联合也是一种特殊的自定义类型,这种类型定义的变量也包含一系列的成员,特征是这些成员公用同一块空间(所以联合也叫共用体)。
比如:
#include <stdio.h>
union Un
{
char c;
int i;
};
int main()
{
printf("%d\n", sizeof(union Un));//4
union Un un = { 0 };
return 0;
}
4.2 联合的特点
联合的成员是共用同一块内存空间的,这样一个联合变量的大小,至少是最大成员的大小(因为联合至少得有能力保存最大的那个成员)。
#include <stdio.h>
union Un
{
char c;
int i;
};
int main()
{
union Un un = { 0 };
printf("%p\n", &un);
printf("%p\n", &un.i);
printf("%p\n", &un.c);
//以上三个地址是一样的
un.i = 0x11223344;
un.c = 0x55;
return 0;
}

有这样一道题目:
判断当前计算机的大小端存储
#include <stdio.h>
union Un
{
int i;
char c;
};
int main()
{
union Un u = { 0 };
u.i = 1;
if (1 == u.c)
{
printf("小端\n");
}
else
{
printf("大端\n");
}
return 0;
}
#include <stdio.h>
int check_sys()
{
union
{
int i;
char c;
}un = { .i = 1 };
return un.c;
}
int main()
{
int ret = check_sys();
if (1 == ret)
{
printf("小端\n");
}
else
{
printf("大端\n");
}
return 0;
}
4.3 联合大小的计算
- 联合的大小至少是最大成员的大小。
- 当最大成员大小不是最大对齐数的整数倍的时候,就要对齐到最大对齐数的整数倍。
比如:
#include <stdio.h>
union Un1
{
char c[5];//1 8 1 5
int i;//4 8 4
};
union Un2
{
short c[7];//2 8 2 14
int i;//4 8 4
};
int main()
{
printf("%d\n", sizeof(union Un1));//8
printf("%d\n", sizeof(union Un2));//16
return 0;
}