声明,本文部分内容摘自:
Go: 深入理解堆实现及应用-腾讯云开发者社区-腾讯云
数组实现堆 | WXue

堆(Heap)是实现优先队列的数据结构,Go提供了接口和方法来操作堆。
应用
package main
import (
"container/heap"
"sort"
)
/*
题目:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。
你只可以看到在滑动窗口内的 k 个数字,滑动窗口每次只向右移动一位,返回滑动窗口中的最大值。
示例:
输入:
nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:
[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
---------------------------------
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
题解:
大根堆可以帮助我们实时维护一系列元素中的最大值。
初始时,我们将数组 nums 的前 k 个元素放入优先队列中。
每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。
然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。
因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除。
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。
为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 (num,index),表示元素 num 在数组中的下标为 index。
*/
var a []int
// heap 实现了标准库的heap.Interface接口
type hp struct {
sort.IntSlice // type IntSlice []int
}
func (h hp) Less(i, j int) bool {
return a[h.IntSlice[i]] > a[h.IntSlice[j]]
}
func (h *hp) Push(v interface{}) {
h.IntSlice = append(h.IntSlice, v.(int))
}
func (h *hp) Pop() interface{} {
a := h.IntSlice
v := a[len(a)-1]
h.IntSlice = a[:len(a)-1]
return v
}
func maxSlidingWindow(nums []int, k int) (ans []int) {
ans = make([]int, 1, len(nums)-k+1)
a = nums
// 初始化堆(优先队列)
queue := &hp{make([]int, k)} // 优先队列
for i := 0; i < k; i++ {
queue.IntSlice[i] = i // 注意堆里存的是数组下标而非数组值,对应Less函数里的比较时需要a[h.IntSlice[i]]来比较值
}
heap.Init(queue) // 初始化+向下调整
// 赋值ans[0],因为不需要判断IntSlice[0]的元素是不是在边界外的左侧
ans[0] = nums[queue.IntSlice[0]] // IntSlice[0] 下标为0=数组IntSlice的头部=堆顶元素
// 窗口滑动
for i := k; i < len(nums); i++ {
heap.Push(queue, i) // 入堆+向上调整
for queue.IntSlice[0] <= i-k { // 判断IntSlice[0]的元素是不是在边界外的左侧
heap.Pop(queue) // 出堆+向下调整
}
ans = append(ans, nums[queue.IntSlice[0]]) // IntSlice[0] 下标为0=数组头部=堆顶元素
}
return ans
}
func main() {
res := maxSlidingWindow([]int{1, 3, -1, -3, 5, 3, 6, 7}, 3)
println(res)
}
底层
包:container/heap
接口:heap.Interface
源码:
type Interface interface {
sort.Interface
Push(x interface{}) // 添加元素
Pop() interface{} // 弹出元素
}其中,注意,实现heap.Interface接口需要嵌入sort.Interface,后者包含Len()、Less(i, j int) bool和Swap(i, j int)方法,用于确定元素间的排序。
全部源码:
type Interface interface {
sort.Interface
Push(x any) // add x as element Len()
Pop() any // remove and return element Len() - 1.
}
func Init(h Interface) {
// heapify
n := h.Len()
for i := n/2 - 1; i >= 0; i-- {
down(h, i, n)
}
}
// Push pushes the element x onto the heap.
// The complexity is O(log n) where n = h.Len().
func Push(h Interface, x any) {
h.Push(x)
up(h, h.Len()-1)
}
func Pop(h Interface) any {
n := h.Len() - 1
h.Swap(0, n)
down(h, 0, n)
return h.Pop()
}
func Remove(h Interface, i int) any {
n := h.Len() - 1
if n != i {
h.Swap(i, n)
if !down(h, i, n) {
up(h, i)
}
}
return h.Pop()
}
func Fix(h Interface, i int) {
if !down(h, i, h.Len()) {
up(h, i)
}
}
func up(h Interface, j int) {
for {
i := (j - 1) / 2 // parent
if i == j || !h.Less(j, i) {
break
}
h.Swap(i, j)
j = i
}
}
func down(h Interface, i0, n int) bool {
i := i0
for {
j1 := 2*i + 1
if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
break
}
j := j1 // left child
if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
j = j2 // = 2*i + 2 // right child
}
if !h.Less(j, i) {
break
}
h.Swap(i, j)
i = j
}
return i > i0
}其中:
① 初始化(Init): 对一个未排序的切片构建堆。这是通过down方法实现的,down方法确保元素下沉到正确的位置,维持堆的性质。
② 添加元素(Push): 元素被添加到切片的末尾,然后通过up方法上浮到正确的位置。
注意:标准库中的push函数中,第一行调用的【h.Push(x)】是上层业务代码中自行实现的heap.Interface的堆实例的push方法。
func Push(h Interface, x any) {
h.Push(x)
up(h, h.Len()-1)
}
③ 删除元素(Pop): 堆顶元素(切片的第一个元素)被移动到切片末尾并返回,然后新的堆顶元素通过down方法恢复堆的性质。
④ 删除任意元素(Remove): 类似Pop,但可以移除指定位置的元素。此操作需要综合up和down方法来调整堆。
⑤ 修改元素并调整堆(Fix): 如果堆中某个元素被外部修改了(比如优先级改变),Fix方法会根据这个修改后的新值重新调整堆。
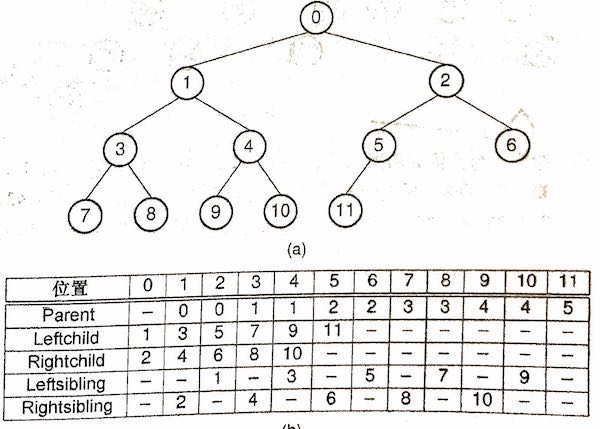
堆是一颗完全二叉树,可由数组表示
完全二叉树,逐层而下,从左到右,结点的位置完全由其序号觉得,因此可以用数组来实现。
计算各结点下标的公式,其中 𝑟𝑟 表示结点的下标,范围在 0 ~ n-1 之间,n 是二叉树结点的总数。
𝑃𝑎𝑟𝑒𝑛𝑡(𝑟)=⌊(𝑟−1)/2⌋𝑃𝑎𝑟𝑒𝑛𝑡(𝑟)=⌊(𝑟−1)/2⌋ 向下取整,当 𝑟≠0𝑟≠0 时
𝐿𝑒𝑓𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+1𝐿𝑒𝑓𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+1, 当 2𝑟+1<𝑛2𝑟+1<𝑛 时
𝑅𝑖𝑔ℎ𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+2𝑅𝑖𝑔ℎ𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+2, 当 2𝑟+2<𝑛2𝑟+2<𝑛 时
𝐿𝑒𝑓𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟−1𝐿𝑒𝑓𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟−1, 当 r 为偶数时
𝑅𝑖𝑔ℎ𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟+1𝑅𝑖𝑔ℎ𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟+1 , 当 r 为奇数并且 𝑟+1<𝑛𝑟+1<𝑛 时
插入数值:在堆的末尾插入,然后不断向上提升,直到没有大小颠倒。
删除数值:首先把堆的最后一个节点的数值放到根上去,并且删除最后一个节点,然后不断向下交换直到没有大小颠倒为止。向下交换的时候如果 2 个儿子都比自己小,那么选择数值较小的儿子进行交换。
复杂度:建堆需要 On 的时间,但删除、插入都和树深度成正比,时间复杂度是 O𝑛𝑙𝑜𝑔𝑛。