今天我带来链式二叉树的代码总结。
目录
- 前言
- 链式二叉树代码实现的五个文档
- 二叉树的例子
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 求结点个数的函数
- 求叶子的个数的函数
- 求k层结点个数的函数
- 查找某一个值的函数
- 求二叉树高度的函数
- 判断二叉树是否是完全二叉树的函数
- 开辟二叉树结点的函数
- 销毁二叉树的函数
- test.c文档的代码
- Binary Tree.c文档的代码
- Binary Tree.h文档的代码
- 链式二叉树的代码的运行结果
- 代码库:[链接](https://gitee.com/guangdong-xiaobit/preliminary-data-structure/tree/master/Binary%20Tree/Binary%20Tree)
前言
在下面的代码中,不采用函数来创建二叉树,在高阶数据结构再来写创建二叉树的函数,并且由于c没有队列,所以还要造个队列来调用,检验代码也不再以菜单的形式。在下面的代码中,我取出链式二叉树的代码,队列的代码包含在完整版,与前面文章有些不同,可在文章后面进去我的代码仓库中获取。
链式二叉树代码实现的五个文档
Queue.h-----队列的头文件引用和函数声明
Queue.c-----队列的函数实现
Binary Tree.h-----链式二叉树的头文件引用和函数声明
Binary Tree.c-----链式二叉树的函数实现
test.c-----链式二叉树代码的检验
二叉树的例子
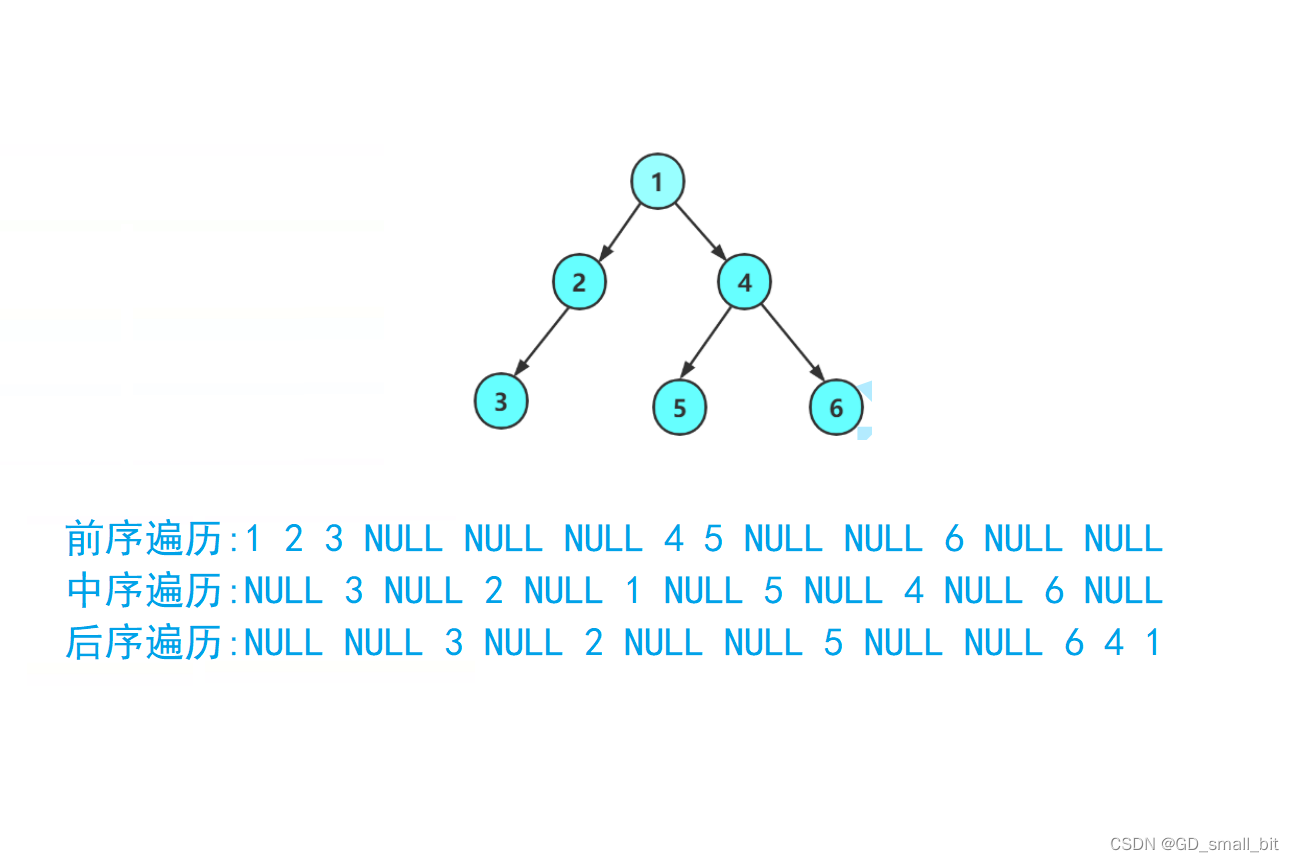
我将采用上面的二叉树进行检验代码。
前序遍历
//前序遍历
void PrevOrder(BinaryTree* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ",root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
中序遍历
//中序遍历
void InOrder(BinaryTree* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ",root->data);
InOrder(root->right);
}
后序遍历
//后序遍历
void PostOrder(BinaryTree* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ",root->data);
}
层序遍历
//层序遍历
void LevelOrder(BinaryTree* root)
{
assert(root);
Queue q;
InitQueue(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BinaryTree* Front = QueueFront(&q);
printf("%d ",Front->data);
QueuePop(&q);
if (Front->left)
QueuePush(&q, Front->left);
if (Front->right)
QueuePush(&q,Front->right);
}
printf("\n");
DestroyQueue(&q);
}
求结点个数的函数
//求结点的个数
int Treesize(BinaryTree* root)
{
if (root == NULL)
return 0;
return Treesize(root->left) + Treesize(root->right) + 1;
}
求叶子的个数的函数
//求叶子的个数
int TreeLeafSize(BinaryTree* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
求k层结点个数的函数
//求第k层结点的个数
int TreeKSize(BinaryTree* root,int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeKSize(root->left,k - 1) + TreeKSize(root->right,k - 1);
}
查找某一个值的函数
//查找某一个值
BinaryTree* TreeFind(BinaryTree* root,BinaryTreeDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BinaryTree* ret1 = TreeFind(root->left,x);
if (ret1)
return ret1;
BinaryTree* ret2 = TreeFind(root->right,x);
if (ret2)
return ret2;
}
求二叉树高度的函数
//求二叉树的高度
int TreeHeight(BinaryTree* root)
{
if (root == NULL)
return 0;
int TreeLeftHeight = TreeHeight(root->left);
int TreeRightHeight = TreeHeight(root->right);
return TreeLeftHeight > TreeRightHeight ? TreeLeftHeight + 1 : TreeRightHeight + 1;
}
判断二叉树是否是完全二叉树的函数
//判断二叉树是否是完全二叉树
bool TreeComplete(BinaryTree* root)
{
Queue q;
InitQueue(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
QueueDataType Front = QueueFront(&q);
QueuePop(&q);
if (Front == NULL)
{
break;
}
else
{
QueuePush(&q,Front->left);
QueuePush(&q,Front->right);
}
}
//出到空以后,如果后面全是空,则是完全二叉树
while (!QueueEmpty(&q))
{
QueueDataType Front = QueueFront(&q);
QueuePop(&q);
if (Front != NULL)
return false;
}
return true;
DestroyQueue(&q);
}
开辟二叉树结点的函数
//开辟结点
BinaryTree* BuyTreeNode(BinaryTreeDataType x)
{
BinaryTree* NewNode = (BinaryTree*)malloc(sizeof(BinaryTree));
if (NewNode == NULL)
{
perror("malloc fail");
exit(1);
}
NewNode->left = NULL;
NewNode->right = NULL;
NewNode->data = x;
}
销毁二叉树的函数
//销毁二叉树
void DestroyBTree(BinaryTree* root)
{
if (root == NULL)
return;
DestroyBTree(root->left);
DestroyBTree(root->right);
free(root);
}
test.c文档的代码
#include "Binary Tree.h"
int main()
{
BinaryTree* n1 = BuyTreeNode(1);
BinaryTree* n2 = BuyTreeNode(2);
BinaryTree* n3 = BuyTreeNode(3);
BinaryTree* n4 = BuyTreeNode(4);
BinaryTree* n5 = BuyTreeNode(5);
BinaryTree* n6 = BuyTreeNode(6);
BinaryTree* n7 = BuyTreeNode(7);
n1->left = n2;
n1->right = n4;
n2->left = n3;
//接上则为完全二叉树
//n2->right = n7;
n4->left = n5;
n4->right = n6;
PrevOrder(n1);
printf("\n");
InOrder(n1);
printf("\n");
PostOrder(n1);
printf("\n");
LevelOrder(n1);
printf("\n");
printf("结点个数:%d\n", Treesize(n1));
printf("叶子的个数:%d\n", TreeLeafSize(n1));
printf("第三层的结点的个数:%d\n", TreeKSize(n1,3));
printf("结点2的地址是:%p\n", TreeFind(n1,2));
printf("二叉树的高度为:%d\n", TreeHeight(n1));
printf("二叉树是否是平衡二叉树:%d", TreeComplete(n1));
DestroyBTree(n1);
}
Binary Tree.c文档的代码
#include "Binary Tree.h"
//前序遍历
void PrevOrder(BinaryTree* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ",root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
//中序遍历
void InOrder(BinaryTree* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ",root->data);
InOrder(root->right);
}
//后序遍历
void PostOrder(BinaryTree* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ",root->data);
}
//层序遍历
void LevelOrder(BinaryTree* root)
{
assert(root);
Queue q;
InitQueue(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BinaryTree* Front = QueueFront(&q);
printf("%d ",Front->data);
QueuePop(&q);
if (Front->left)
QueuePush(&q, Front->left);
if (Front->right)
QueuePush(&q,Front->right);
}
printf("\n");
DestroyQueue(&q);
}
//求结点的个数
int Treesize(BinaryTree* root)
{
if (root == NULL)
return 0;
return Treesize(root->left) + Treesize(root->right) + 1;
}
//求叶子的个数
int TreeLeafSize(BinaryTree* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//求第k层结点的个数
int TreeKSize(BinaryTree* root,int k)
{
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeKSize(root->left,k - 1) + TreeKSize(root->right,k - 1);
}
//查找某一个值
BinaryTree* TreeFind(BinaryTree* root,BinaryTreeDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BinaryTree* ret1 = TreeFind(root->left,x);
if (ret1)
return ret1;
BinaryTree* ret2 = TreeFind(root->right,x);
if (ret2)
return ret2;
}
//求二叉树的高度
int TreeHeight(BinaryTree* root)
{
if (root == NULL)
return 0;
int TreeLeftHeight = TreeHeight(root->left);
int TreeRightHeight = TreeHeight(root->right);
return TreeLeftHeight > TreeRightHeight ? TreeLeftHeight + 1 : TreeRightHeight + 1;
}
//判断二叉树是否是完全二叉树
bool TreeComplete(BinaryTree* root)
{
Queue q;
InitQueue(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
QueueDataType Front = QueueFront(&q);
QueuePop(&q);
if (Front == NULL)
{
break;
}
else
{
QueuePush(&q,Front->left);
QueuePush(&q,Front->right);
}
}
//出到空以后,如果后面全是空,则是完全二叉树
while (!QueueEmpty(&q))
{
QueueDataType Front = QueueFront(&q);
QueuePop(&q);
if (Front != NULL)
return false;
}
return true;
DestroyQueue(&q);
}
//开辟结点
BinaryTree* BuyTreeNode(BinaryTreeDataType x)
{
BinaryTree* NewNode = (BinaryTree*)malloc(sizeof(BinaryTree));
if (NewNode == NULL)
{
perror("malloc fail");
exit(1);
}
NewNode->left = NULL;
NewNode->right = NULL;
NewNode->data = x;
}
//销毁二叉树
void DestroyBTree(BinaryTree* root)
{
if (root == NULL)
return;
DestroyBTree(root->left);
DestroyBTree(root->right);
free(root);
}
Binary Tree.h文档的代码
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include "Queue.h"
typedef int BinaryTreeDataType;
typedef struct BinaryTree
{
BinaryTreeDataType data;
struct BinaryTree* left;
struct BinaryTree* right;
}BinaryTree;
//前序遍历
void PrevOrder(BinaryTree* root);
//中序遍历
void InOrder(BinaryTree* root);
//后序遍历
void PostOrder(BinaryTree* root);
//层序遍历
void LevelOrder(BinaryTree* root);
//求结点的个数
int Treesize(BinaryTree* root);
//求叶子的个数
int TreeLeafSize(BinaryTree* root);
//求第k层结点的个数
int TreeKSize(BinaryTree* root,int k);
//查找某一个值
BinaryTree* TreeFind(BinaryTree* root,BinaryTreeDataType x);
//求二叉树的高度
int TreeHeight(BinaryTree* root);
//判断二叉树是否是完全二叉树
bool TreeComplete(BinaryTree* root);
//开辟结点
BinaryTree* BuyTreeNode(BinaryTreeDataType x);
//销毁二叉树
void DestroyBTree(BinaryTree* root);
链式二叉树的代码的运行结果
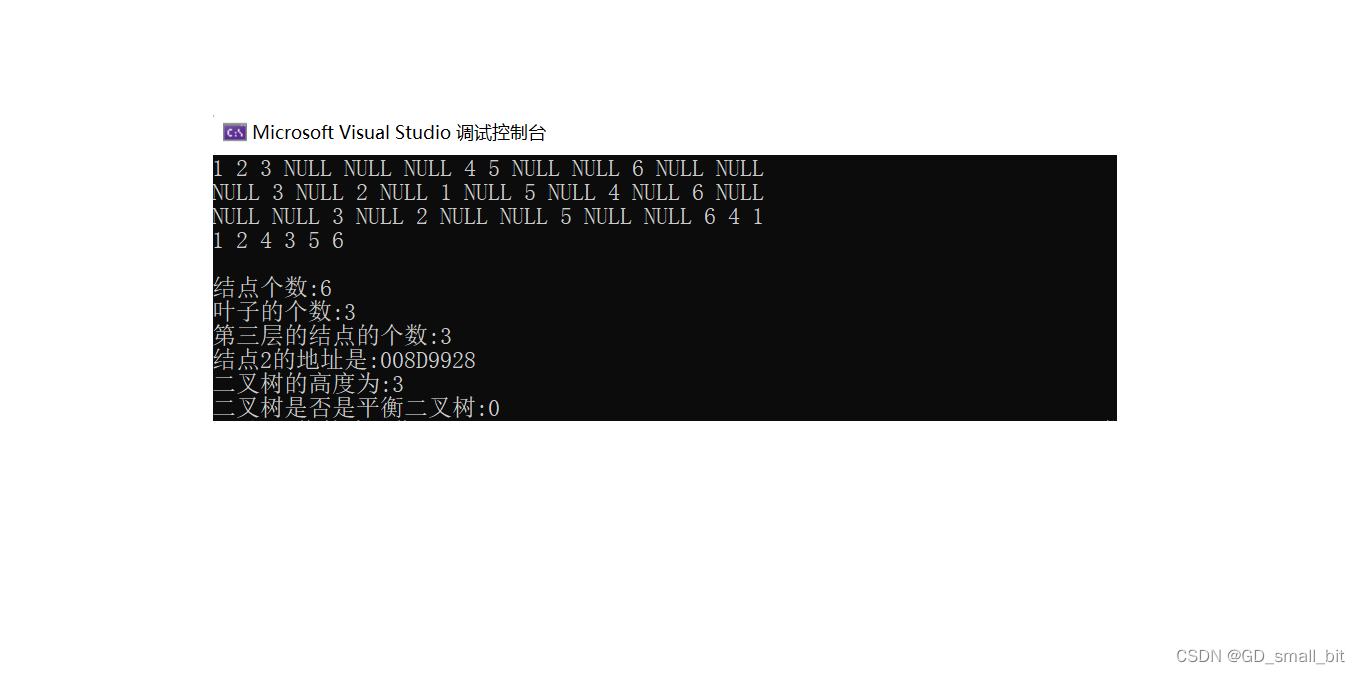
在这些运行结果中,除了求结点2的地址外,其他都可以通过文章上面的二叉树的图进行验证,结点2的地址可以通过调试进行验证,注意每次运行后,结点2的地址都会是不同的。
代码库:链接
今天链式二叉树的代码就讲到这里,关注点一点,下期更精彩。