文章目录
- 前言
- 一、OFDM 信号及模糊函数
- 1、OFDM 信号表达式
- 2、模糊函数表达式
- 二、MATLAB 仿真
- 1、MATLAB 核心源码
- 2、仿真结果
- ①、OFDM 模糊函数
- ②、OFDM 距离模糊函数
- ③、OFDM 速度模糊函数
前言
本文进行 OFDM 的仿真,首先看一下 OFDM 的模糊函数仿真效果:
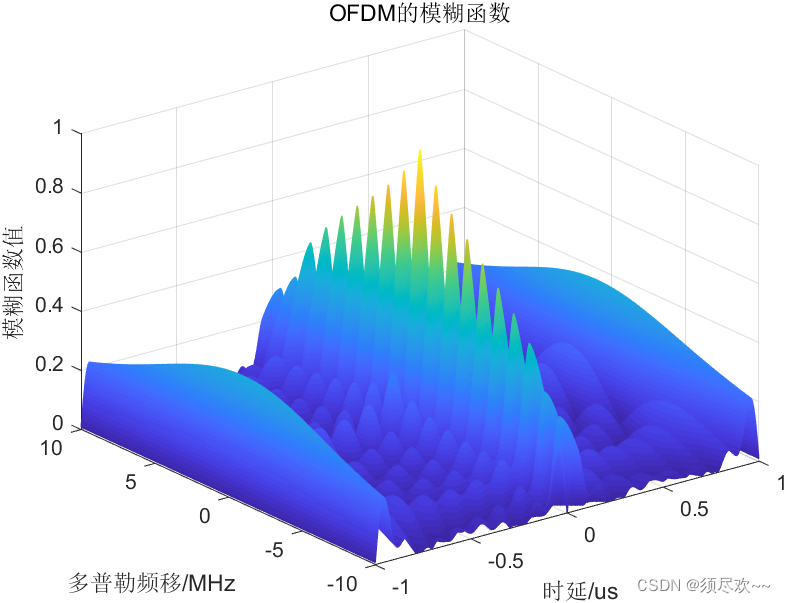
一、OFDM 信号及模糊函数
1、OFDM 信号表达式
OFDM 信号提供了一种在频域上设计波形、时域上输出波形的 DFT 数字调制方式。OFDM 信号的数学表达式为:
B
(
t
)
=
∑
k
=
0
N
−
1
b
k
e
j
2
π
f
k
t
=
∑
k
=
0
N
−
1
b
k
e
j
2
π
(
f
0
+
k
Δ
f
)
t
B(t)=\sum_{k=0}^{N-1}b_ke^{j2\pi f_kt}=\sum_{k=0}^{N-1}b_ke^{j2\pi (f_0+k\Delta f)t}
B(t)=k=0∑N−1bkej2πfkt=k=0∑N−1bkej2π(f0+kΔf)t
- b k :调制序列,为第 k 路子信道中的复输入数据 b_k:调制序列,为第 k 路子信道中的复输入数据 bk:调制序列,为第k路子信道中的复输入数据
- f k = f 0 + k Δ f f_k=f_0+k \Delta f fk=f0+kΔf, f 0 f_0 f0 为起始频率, Δ f \Delta f Δf 为频率间隔
2、模糊函数表达式
模糊函数是雷达探测波形分析的重要工具,通过对信号波形的模糊函数分析,可以得到信号波形的距离分辨率、多普勒分辨率及多普勒容限特性。
为了分析在不同的时延和多普勒频移条件下接收信号与匹配滤波器的不匹配程度,定义了模糊度函数。
连续时间信号模糊函数的定义为:
χ
(
τ
,
f
d
)
=
1
E
∫
−
∞
∞
b
(
t
)
b
∗
(
t
−
τ
)
e
j
2
π
f
d
t
d
t
\chi (\tau,f_d)=\frac{1}{E} \int_{-\infty}^{\infty} b(t)b^{*}(t-\tau)e^{j2\pi f_dt} \,dt
χ(τ,fd)=E1∫−∞∞b(t)b∗(t−τ)ej2πfdtdt
- 式中,E为信号的总能量;
离散时间序列的模糊函数表示为:
χ
(
m
,
k
d
)
=
1
E
c
∑
n
e
n
e
n
−
m
∗
e
j
2
π
N
k
d
n
\chi (m,k_d)=\frac{1}{E_c}\sum_{n}e_ne^{*}_{n-m}e^{j\frac{2\pi}{N}k_dn}
χ(m,kd)=Ec1n∑enen−m∗ejN2πkdn
- 式中, m = f s × τ m=f_s×\tau m=fs×τ, f s f_s fs 为采样率;
- k d = f d × f s N k_d=\frac{f_d×f_s}{N} kd=Nfd×fs,N为采样点数
二、MATLAB 仿真
1、MATLAB 核心源码
%% ofdm信号产生
for j = 0:N_symbol - 1 % 用于处理每个相位编码
for k = 0:M-1 % 用于处理每个子载波
for n = 0:N-1 % 用于生成每个时刻的样本
x_tmp(k+1,n+1+j*N) = tx_data(k+1+j*N)*exp(1j*2*pi*k*n/N);
end
end
end
2、仿真结果
①、OFDM 模糊函数
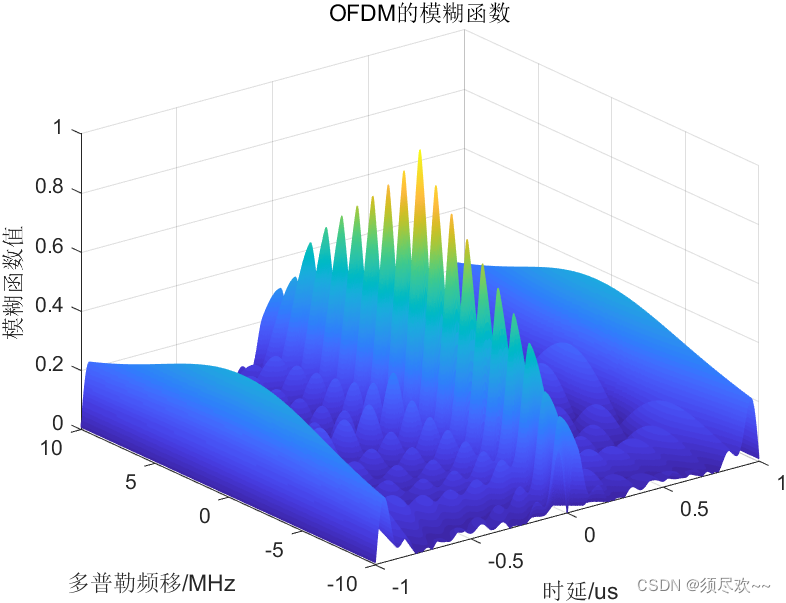
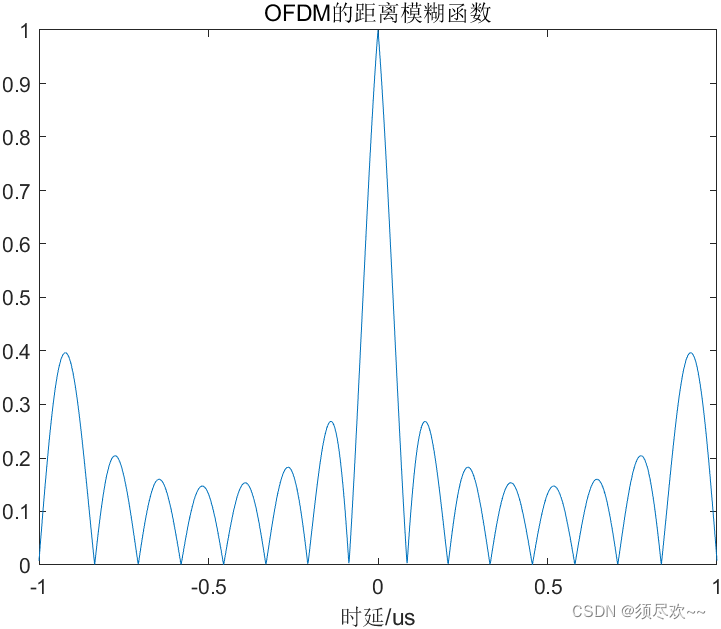
②、OFDM 距离模糊函数
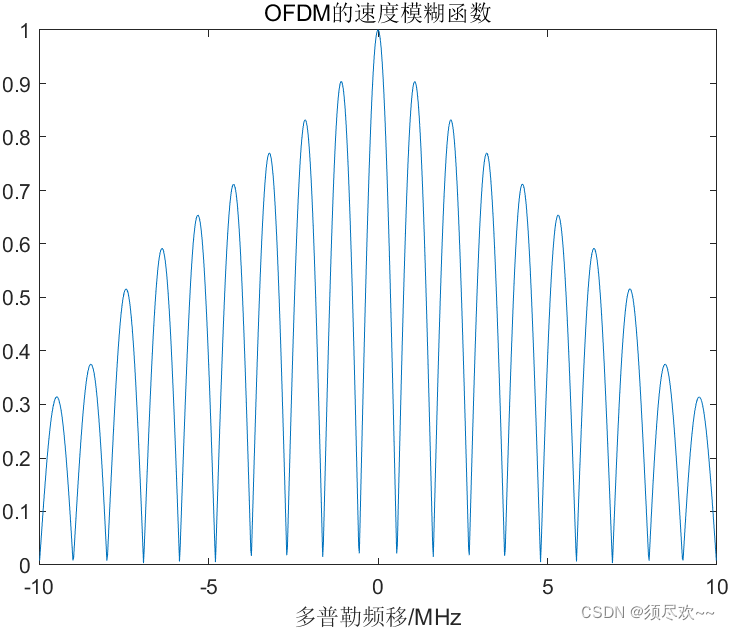
③、OFDM 速度模糊函数
我的qq:2442391036,欢迎交流!

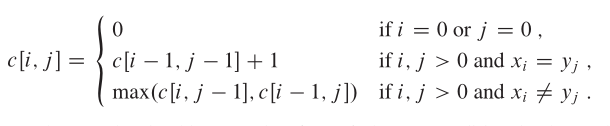




![[ROS2] --- 通信接口](https://img-blog.csdnimg.cn/direct/78d6260117384619a54a1c86ffd546f0.png)