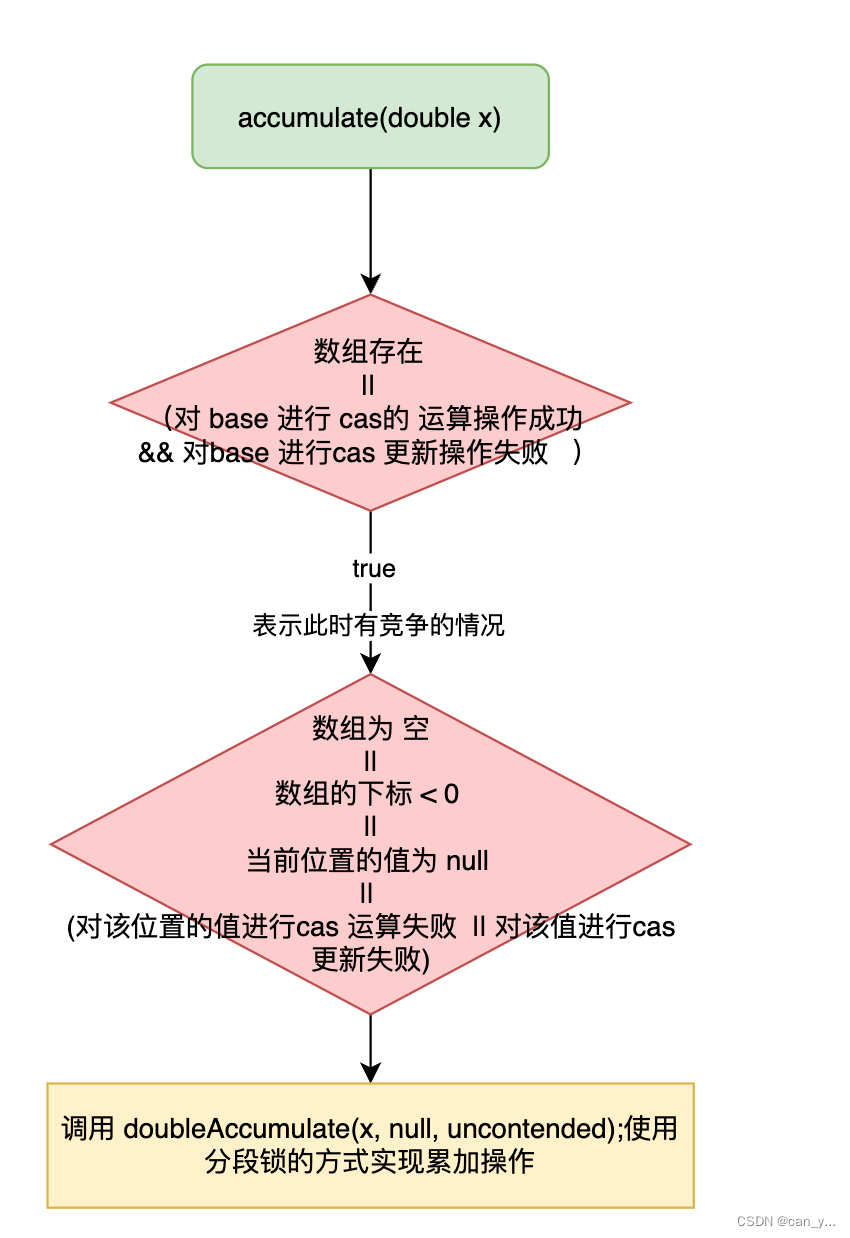
题目描述：

如果Z既是X的子串，又是Y的子串，则称Z为X和Y的公共子串。

如果给定X、Y，求出最长Z及其长度。

注意：这里求的不是子序列，两者的意思并不相同。子串要求连续，子序列并不需要。

如果想要了解可以看这一篇最长子序列问题（LCS）--动态规划解法

示例：

输入

ABACCB

AACCAB

输出

ACC

3

分析：

dp[i][j]表示X从0到i与Y从0到j之间公共子串的长度。

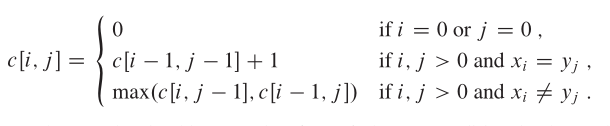
代码：

 

//最长字串问题,不是最长子序列问题
#include<iostream>
#include<string>
using namespace std;

const int N = 1000;
int dp[N][N] = { 0 };

int  main()
{
	string a, b;
	cin >> a;
	cin >> b;
	int lena = a.size();
	int lenb = b.size();
	int maxLen = 0;//最长字串长度
	int start = 0;//最长字串在a中的初始下标


	//本来要将dp[i][0]和dp[0][j]全都初始化，但是因为是0，所以可以省略
	//直接dp
	for (int i = 0; i <lena; i++)
	{
		for (int j = 0; j <lenb; j++)
		{
			if (a[i] == b[j])
			{
				if (i > 0 && j > 0)
				{
					dp[i][j] = dp[i - 1][j - 1] + 1;
				}
				else
				{
					dp[i][j] = 1;
				}
			}

			//如果a[i]!=b[i]，则dp[i][j] = 0
			//这是因为子串要连续，走到i,j就断了这个连续。
			else
			{
				dp[i][j] = 0;//这步可以省略，因为初始值就是0；
			}

			if (dp[i][j] > maxLen)
			{
				maxLen = dp[i][j];//更新最长字串长度
				start = i - maxLen + 1;//记录最长字串在a中的初始下标
			}
		}
	}

	cout << "dp数组为：" << endl;
	for (int i = 0; i < lena; i++)
	{
		for (int j = 0; j < lenb; j++)
		{
			cout << dp[i][j] << ' ';
		}
		cout << endl;
	}
	cout << "最长子串长度为：" << maxLen << endl;
	cout << "最长子串为" << a.substr(start, maxLen) << endl;
	system("pause");
	return 0;

}