最终效果

先看下最终效果：

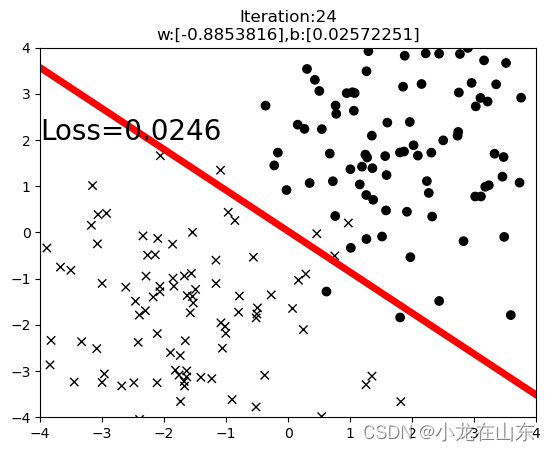
这里用一条直线把二维平面上不同的点分开。

生成随机数据

#创建训练数据
x = torch.rand(10,1)*10 #shape(10,1)
y = 2*x + (5 + torch.randn(10,1))


#构建线性回归参数
w = torch.randn((1))#随机初始化w，要用到自动梯度求导
b = torch.zeros((1))#使用0初始化b，要用到自动梯度求导

n_data = torch.ones(100, 2)
xy0 = torch.normal(2 * n_data, 1.5)  # 生成均值为2.标准差为1.5的随机数组成的矩阵
c0 = torch.zeros(100)
xy1 = torch.normal(-2 * n_data, 1.5)  # 生成均值为-2.标准差为1.5的随机数组成的矩阵
c1 = torch.ones(100)

x,y = torch.cat((xy0,xy1),0).type(torch.FloatTensor).split(1, dim=1)
x = x.squeeze()
y = y.squeeze()
c = torch.cat((c0,c1),0).type(torch.FloatTensor)

数据可视化

def plot(x, y, c):
    ax = plt.gca()
    sc = ax.scatter(x, y, color='black')
    paths = []
    for i in range(len(x)):
        if c[i].item() == 0:
            marker_obj = mmarkers.MarkerStyle('o')
        else:
            marker_obj = mmarkers.MarkerStyle('x')
        path = marker_obj.get_path().transformed(marker_obj.get_transform())
        paths.append(path)
    sc.set_paths(paths)
    return sc
plot(x, y, c)
plt.show()

使用x和o来表示两种不同类别的数据。

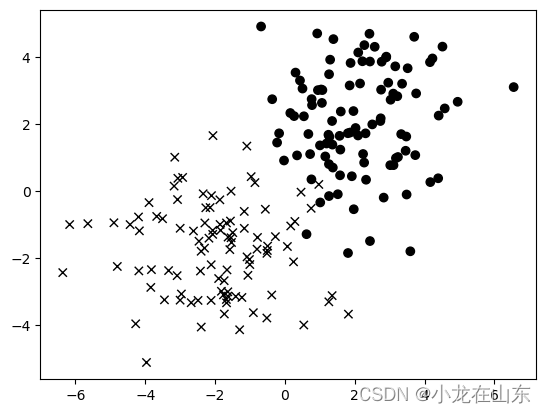
定义模型和损失函数

#构建逻辑回归参数
w = torch.tensor([1.,],requires_grad=True)  # 随机初始化w
b = torch.zeros((1),requires_grad=True)  # 使用0初始化b

wx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + b
loss = (0.5*(y-y_pred)**2).mean()

这里使用了平方损失函数来估算模型准确度。

训练模型

最多训练100次，每次都会更新模型参数，当损失值小于0.03时停止训练。

xx = torch.arange(-4, 5)
lr = 0.02 #学习率
for iteration in range(100):
    #前向传播
    loss = ((torch.sigmoid(x*w+b-y) - c)**2).mean()
    #反向传播
    loss.backward()
    #更新参数
    b.data.sub_(lr*b.grad) # b = b - lr*b.grad
    w.data.sub_(lr*w.grad) # w = w - lr*w.grad
    #绘图
    if iteration % 3 == 0:
        plot(x, y, c)
        yy = w*xx + b
        plt.plot(xx.data.numpy(),yy.data.numpy(),'r-',lw=5)
        plt.text(-4,2,'Loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'black'})
        plt.xlim(-4,4)
        plt.ylim(-4,4)
        plt.title("Iteration:{}\nw:{},b:{}".format(iteration,w.data.numpy(),b.data.numpy()))
        plt.show()

        if loss.data.numpy() < 0.03:  # 停止条件
            break

全部代码

import torch
import matplotlib.pyplot as plt
import matplotlib.markers as mmarkers

#创建训练数据
x = torch.rand(10,1)*10 #shape(10,1)
y = 2*x + (5 + torch.randn(10,1))


#构建线性回归参数
w = torch.randn((1))#随机初始化w，要用到自动梯度求导
b = torch.zeros((1))#使用0初始化b，要用到自动梯度求导

wx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + b


n_data = torch.ones(100, 2)
xy0 = torch.normal(2 * n_data, 1.5)  # 生成均值为2.标准差为1.5的随机数组成的矩阵
c0 = torch.zeros(100)
xy1 = torch.normal(-2 * n_data, 1.5)  # 生成均值为-2.标准差为1.5的随机数组成的矩阵
c1 = torch.ones(100)

x,y = torch.cat((xy0,xy1),0).type(torch.FloatTensor).split(1, dim=1)
x = x.squeeze()
y = y.squeeze()
c = torch.cat((c0,c1),0).type(torch.FloatTensor)


def plot(x, y, c):
    ax = plt.gca()
    sc = ax.scatter(x, y, color='black')
    paths = []
    for i in range(len(x)):
        if c[i].item() == 0:
            marker_obj = mmarkers.MarkerStyle('o')
        else:
            marker_obj = mmarkers.MarkerStyle('x')
        path = marker_obj.get_path().transformed(marker_obj.get_transform())
        paths.append(path)
    sc.set_paths(paths)
    return sc
plot(x, y, c)
plt.show()


#构建逻辑回归参数
w = torch.tensor([1.,],requires_grad=True)#随机初始化w
b = torch.zeros((1),requires_grad=True)#使用0初始化b

wx = torch.mul(w,x) # w*x
y_pred = torch.add(wx,b) # y = w*x + b
loss = (0.5*(y-y_pred)**2).mean()

xx = torch.arange(-4, 5)
lr = 0.02 #学习率
for iteration in range(100):
    #前向传播
    loss = ((torch.sigmoid(x*w+b-y) - c)**2).mean()
    #反向传播
    loss.backward()
    #更新参数
    b.data.sub_(lr*b.grad) # b = b - lr*b.grad
    w.data.sub_(lr*w.grad) # w = w - lr*w.grad
    #绘图
    if iteration % 3 == 0:
        plot(x, y, c)
        yy = w*xx + b
        plt.plot(xx.data.numpy(),yy.data.numpy(),'r-',lw=5)
        plt.text(-4,2,'Loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'black'})
        plt.xlim(-4,4)
        plt.ylim(-4,4)
        plt.title("Iteration:{}\nw:{},b:{}".format(iteration,w.data.numpy(),b.data.numpy()))
        plt.show()

        if loss.data.numpy() < 0.03:#停止条件
            break