文章目录
- 排列组合
- 2023
- 真题(2023-05)-数据分析-排列组合-组合-C运算-至少-需反面思考
- 真题(2023-08)-数据分析-排列组合-相邻+不相邻-捆绑法+插空法-插空法注意空位比座位多1个,是用A;捆绑法内部排序用A;
- 2022
- 真题(2022-10)-算术-质数+-数据分析-排列组合
- 真题(2022-12)-数据分析-排列组合-闯关题
- 真题(2022-13)-数据分析-排列组合-排队-相邻不相邻-不相邻插空法
- 真题(2022-15)-数据分析-排列组合-涂色
- 2021
- 真题(2021-08)-数据分析-排列组合-计数原理-加法原理
- 2020
- 真题(2020-15)-数据分析-排列组合-不同元素的分配问题
- 2019
- 真题(2019-14)-数据分析-排列组合-组合-C运算
- 2018
- 2017
- 2016
- 2015
- 2014
- 2013
- 概率
- 2023
- 真题(2023-25)-数据分析-概率-已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
- 2022
- 真题(2022-05)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母是C运算,分子数量少用穷举,数量多用C运算
- 2021
- 真题(2021-06)-数据分析-概率已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
- 真题(2021-11)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型??
- 真题(2021-14)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型⟹ 正难则反⟹ 转为一次取球模型⟹ 设口袋中有a个白球,b个黑球,一次取出若干个球,则恰好取了 m ( m ≤ a ) m (m≤a) m(m≤a)个白球, n ( n ≤ b ) n(n≤b) n(n≤b)个黑球的概率是 P = C a m ⋅ C b n C a + b m + n P=\frac{C_a^m·C_b^n}{C_{a+b}^{m+n}} P=Ca+bm+nCam⋅Cbn。
- 2020
- 真题(2020-04)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算;-算术-质数-2,3,5,7,11,13,17,19,23,29;
- 真题(2020-14)-数据分析-概率-已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
- 真题(2020-19)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型⟹ 正难则反⟹ 转为一次取球模型⟹ 设口袋中有a个白球,b个黑球,一次取出若干个球,则恰好取了 m ( m ≤ a ) m (m≤a) m(m≤a)个白球, n ( n ≤ b ) n(n≤b) n(n≤b)个黑球的概率是 P = C a m ⋅ C b n C a + b m + n P=\frac{C_a^m·C_b^n}{C_{a+b}^{m+n}} P=Ca+bm+nCam⋅Cbn。翻译“≥≤”-准确率90%-D:题干或选项可以翻译成≥或≤的,选D
- 2019
- 真题(2019-07)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母是C运算,分子数量少用穷举,数量多用C运算
- 真题(2019-17)-数据分析-概率已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
- 2018
- 2017
- 2016
- 2015
- 2014
- 2013
- 数据描述
- 2023
- 真题(2023-12)-数据分析-数据描述-快速比较方差的大小-极差大的,数据波动大,方差就大;极差小的,数据波动小,方差就小。
- 2022
- 2021
- 2020
- 真题(2020-03)-数据分析-数据描述-平均值
- 真题(2020-09)-数据分析-数据描述-平均值与方差-分歧大不是方差大
- 真题(2020-18)-数据分析-数据描述-平均值与方差
- 2019
- 真题(2019-08)-数据分析-数据描述-方差
- 真题(2019-23)-数据分析-数据描述-平均值
- 2018
- 2017
- 2016
- 2015
- 2014
- 2013
排列组合
2023
真题(2023-05)-数据分析-排列组合-组合-C运算-至少-需反面思考


真题(2023-08)-数据分析-排列组合-相邻+不相邻-捆绑法+插空法-插空法注意空位比座位多1个,是用A;捆绑法内部排序用A;


2022
真题(2022-10)-算术-质数±数据分析-排列组合
10.一个自然数的各位数字都是 105 的质因数,且每个质因数最多出现一次,这样的自然数有( )个。
A.6
B.9
C.12
D.15
E.27

真题(2022-12)-数据分析-排列组合-闯关题
12.甲乙两支足球队进行比赛,比分为 4:2,且在比赛过程中乙队没有领先过,则不同的进球顺序有( )。
A.6 种
B. 8 种
C. 9 种
D. 10 种
E. 12 种

真题(2022-13)-数据分析-排列组合-排队-相邻不相邻-不相邻插空法
13.4 名男生和 2 名女生随机站成一排,则女生既不在两端也不相邻的概率为( )
A.
1
2
\frac{1}{2}
21
B.
5
12
\frac{5}{12}
125
C.
3
8
\frac{3}{8}
83
D.
1
3
\frac{1}{3}
31
E.
1
5
\frac{1}{5}
51

真题(2022-15)-数据分析-排列组合-涂色
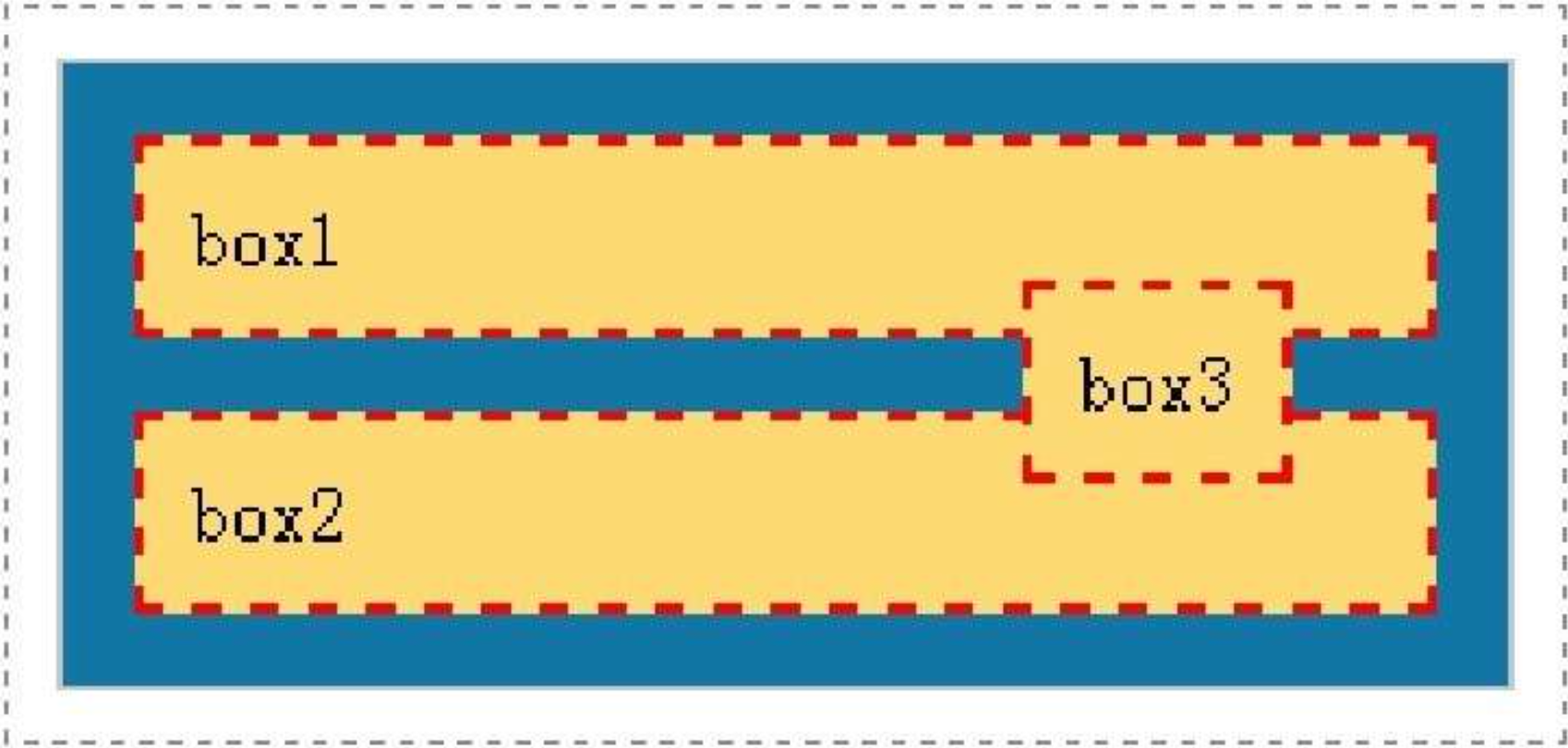
15.如图,用 4 种颜色对图中五块区域进行涂色,每块区域涂一种颜色,且相邻的两块区域颜色不同,不同的涂色方法有( )种
A.12
B.24
C.32
D.48
E.96
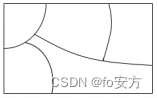

涂色
(1)直线涂色:简单的乘法原理。
(2)环形涂色公式:把一个环形区域分为k块,每块之间首尾相连,用s种颜色去涂,要求相邻两块颜色不同,则不同的涂色方法有
N
=
(
s
—
1
)
k
+
(
s
—
1
)
(
−
1
)
k
N=(s—1)^k+(s—1)(-1)^k
N=(s—1)k+(s—1)(−1)k,式中,s为颜色数(记忆方法:se色),k为环形被分成的块数(记忆方法:kuai 块)。——【环形涂色公式:色减一的块次幂】
2021
真题(2021-08)-数据分析-排列组合-计数原理-加法原理
8.甲.乙两组同学中,甲组有3男3女,乙组有4男2女,从甲、乙两组中各选出2名同学,这4人中恰有1女的选法有( )种。
A.26
B.54
C.70
D.78
E.105

2020
真题(2020-15)-数据分析-排列组合-不同元素的分配问题
15、某科室有 4 名男职员,2 名女职员,若将这 6 名职员分为 3 组,每组两人,且女职员不同组,则分法有( )种
A.4
B.6
C.9
D.12
E.15


2019
真题(2019-14)-数据分析-排列组合-组合-C运算
14、某中学的 5 个学科各推荐 2 名教师作为支教候选人,若从中选出来自不同学科的 2 人参加支教工作,则不同的选派方式有( )种。
A. 20
B. 24
C. 30
D. 40
E. 45

2018
2017
2016
2015
2014
2013
概率
2023
真题(2023-25)-数据分析-概率-已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率


2022
真题(2022-05)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母是C运算,分子数量少用穷举,数量多用C运算
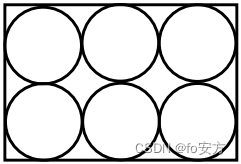
5.如图,已知相邻的圆都相切,从这 6 个圆中随机取 2 个,这 2 个圆不相切的概率为( )
A.
8
15
\frac{8}{15}
158
B.
7
15
\frac{7}{15}
157
C.
3
5
\frac{3}{5}
53
D.
2
5
\frac{2}{5}
52
E.
2
3
\frac{2}{3}
32

2021
真题(2021-06)-数据分析-概率已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
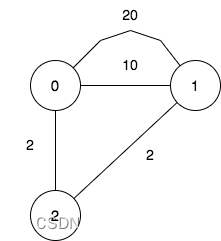
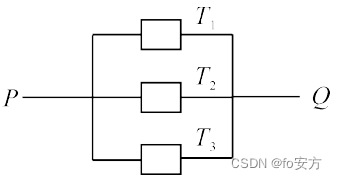
6.如图,由P到Q电路中有三个元件,分别为
T
1
,
T
2
,
T
3
T_1,T_2,T_3
T1,T2,T3,电流能通过
T
1
,
T
2
,
T
3
T_1,T_2,T_3
T1,T2,T3概率分别为0.9,0.9,0.99,假设电流能否通过三个元件相互独立,则电流能在P、Q之间通过的概率是( )。
A.0.8019
B.0.9989
C.0.999
D.0.9999
E.0.99999

真题(2021-11)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型??
11.某商场利用抽奖方式促销,100个奖券中设有3个一等奖,7个二等奖,则一等奖先于二等奖抽完的概率为( )
A.0.3
B.0.5
C.0.6
D.0.7
E.0.73

真题(2021-14)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型⟹ 正难则反⟹ 转为一次取球模型⟹ 设口袋中有a个白球,b个黑球,一次取出若干个球,则恰好取了 m ( m ≤ a ) m (m≤a) m(m≤a)个白球, n ( n ≤ b ) n(n≤b) n(n≤b)个黑球的概率是 P = C a m ⋅ C b n C a + b m + n P=\frac{C_a^m·C_b^n}{C_{a+b}^{m+n}} P=Ca+bm+nCam⋅Cbn。
14.从装有1个红球,2个白球,3个黑球的袋中随机取出3个球,则这3个球的颜色至多有两种的概率( )
A.0.3
B.0.4
C.0.5
D.0.6
E.0.7

2020
真题(2020-04)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算;-算术-质数-2,3,5,7,11,13,17,19,23,29;
4、从 1 至 10 这 10 个整数中任取 3 个数,恰有 1 个质数的概率是( )
A.
2
3
\frac{2}{3}
32
B.
1
2
\frac{1}{2}
21
C.
5
12
\frac{5}{12}
125
D.
2
5
\frac{2}{5}
52
E.
1
120
\frac{1}{120}
1201

真题(2020-14)-数据分析-概率-已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
14.节点 A, B, C, D 两两相连,从一个节点沿线段到另一个节点当作 1 步,若机器人从节点 A出发,随机走了 3 步,则机器人从未经过节点C 的概率为( )
A.
4
9
4\over9
94
B.
11
27
11\over27
2711
C.
10
27
10\over27
2710
D.
19
27
19\over27
2719
E.
8
27
8\over27
278


真题(2020-19)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母有顺序要求是A运算,无顺序是C运算,分子数量少用穷举,数量多用C运算⟹ 袋中取球模型⟹ 正难则反⟹ 转为一次取球模型⟹ 设口袋中有a个白球,b个黑球,一次取出若干个球,则恰好取了 m ( m ≤ a ) m (m≤a) m(m≤a)个白球, n ( n ≤ b ) n(n≤b) n(n≤b)个黑球的概率是 P = C a m ⋅ C b n C a + b m + n P=\frac{C_a^m·C_b^n}{C_{a+b}^{m+n}} P=Ca+bm+nCam⋅Cbn。翻译“≥≤”-准确率90%-D:题干或选项可以翻译成≥或≤的,选D
19、甲、乙两种品牌手机共有 20 部,从中任选 2 部,则恰有 1 部甲品牌手机的概率大于
1
2
1\over2
21。
(1)甲手机不少于 8 部
(2)乙手机大于 7 部


2019
真题(2019-07)-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母是C运算,分子数量少用穷举,数量多用C运算
7、在分别标记 1,2,3,4,5,6 的 6 张卡片,甲抽取一张,乙从余下的卡片中再抽取 2 张,乙的卡片数字之和大于甲的卡片数字的概率为()
A.
11
60
\frac{11}{60}
6011
B.
13
60
\frac{13}{60}
6013
C.
43
60
\frac{43}{60}
6043
D.
47
60
\frac{47}{60}
6047
E.
49
60
\frac{49}{60}
6049
【解析】母题82·古典概型方法一:采用穷举法.
当甲抽取卡片1时,乙有
C
5
2
=
10
C_5^2=10
C52=10(种)选法;
当甲抽取卡片2时,乙有
C
5
2
=
10
C_5^2=10
C52=10(种)选法;
当甲抽取卡片3时,乙有9种选法;
当甲抽取卡片4时,乙有8种选法;
当甲抽取卡片5时,乙有6种选法;
当甲抽取卡片6时,乙有4种选法。
以上合计47种选法。
总的事件数为
C
5
1
C
5
2
=
60
C_5^1C_5^2=60
C51C52=60(种),故所求概率为
47
60
\frac{47}{60}
6047。
方法二:求对立事件
事件总数为
C
5
1
C
5
2
=
60
C_5^1C_5^2=60
C51C52=60(种).
如果甲抽取卡片6,则乙的卡片数字之和小于等于甲的情况有(5,1),(4,2),(4,1),(3,2),(3,1),(1,2),共6种;
如果甲抽取卡片5,则乙的卡片数字之和小于等于甲的情况有(4,1),(3,2),(3,1),(1,2),共4种;
如果甲抽取卡片4,则乙的卡片数字之和小于等于甲的情况有(3,1),(1,2),共2种;
如果甲抽取卡片3,则乙的卡片数字之和小于等于甲的情况有(1,2),共1种。
故所求概率=
1
−
6
+
4
+
2
+
1
60
=
47
60
1-\frac{6+4+2+1}{60}=\frac{47}{60}
1−606+4+2+1=6047,故选(D).


真题(2019-17)-数据分析-概率已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率
17、有甲乙两袋奖券,获奖率分别为 p 和q ,某人从两袋中各随机抽取 1 张奖券,则此人获奖的概率不小于
3
2
\frac{3}{2}
23
(1) 已经
p
+
q
=
1
p + q = 1
p+q=1
(2) 已知
p
q
=
1
4
pq=\frac{1}{4}
pq=41


2018
2017
2016
2015
2014
2013
数据描述
2023
真题(2023-12)-数据分析-数据描述-快速比较方差的大小-极差大的,数据波动大,方差就大;极差小的,数据波动小,方差就小。


2022
2021
2020
真题(2020-03)-数据分析-数据描述-平均值
3、一项考试的总成绩由甲乙丙三部分组成:总成绩=甲成绩×30% +乙成绩×20% +丙成绩×50% ,考试通过的标准是:每部分≥50 分,且总成绩≥60 分。已知某人甲成绩 70 分,乙成绩 75 分,且通过了这项考试,则此人丙成绩的分数至少是( )
A.48
B.50
C.55
D.60
E.62


真题(2020-09)-数据分析-数据描述-平均值与方差-分歧大不是方差大
9、某人在同一观众群中调查了对五部电影的看法,得到如下数据:
| 电影 | 第一部 | 第二部 | 第三部 | 第四部 | 第五部 |
|---|---|---|---|---|---|
| 好评率 | 0.25 | 0.5 | 0.3 | 0.8 | 0.4 |
| 差评率 | 0.75 | 0.5 | 0.7 | 0.2 | 0.6 |
据此数据,观众意见分歧较大的两部影片依次是( )
A.一三
B.二三
C.二五
D.四一
E.四二


真题(2020-18)-数据分析-数据描述-平均值与方差
18、若a, b, c 是实数,则能确定a, b, c 的最大值。
(1)已知a, b, c 的平均值。
(2)已知a, b, c 的最小值。


2019
真题(2019-08)-数据分析-数据描述-方差
8、10 名同学的语文和数学成绩如表
| 语文成绩 | 90 | 92 | 94 | 88 | 86 | 95 | 87 | 89 | 91 | 93 |
|---|---|---|---|---|---|---|---|---|---|---|
| 数学成绩 | 94 | 88 | 96 | 93 | 90 | 85 | 84 | 80 | 82 | 98 |
语文和数学成绩的均值分别为
E
1
E_1
E1 和
E
2
E_2
E2 ,标准差分别为
σ
1
σ_1
σ1和
σ
2
σ_2
σ2,则
A.
E
1
>
E
2
,
σ
1
>
σ
2
E_1>E_2,σ_1>σ_2
E1>E2,σ1>σ2
B.
E
1
>
E
2
,
σ
1
<
σ
2
E_1>E_2,σ_1<σ_2
E1>E2,σ1<σ2
C.
E
1
>
E
2
,
σ
1
=
σ
2
E_1>E_2,σ_1=σ_2
E1>E2,σ1=σ2
D.
E
1
<
E
2
,
σ
1
>
σ
2
E_1<E_2,σ_1>σ_2
E1<E2,σ1>σ2
E.
E
1
<
E
2
,
σ
1
<
σ
2
E_1<E_2,σ_1<σ_2
E1<E2,σ1<σ2
【解析】母题99·图像图表问题+母题18·平均值与方差
E
1
=
90
+
92
+
94
+
88
+
86
+
95
+
87
+
89
+
91
+
93
10
=
90.5
E_1=\frac{90+92+94+88+86+95+87+89+91+93}{10}=90.5
E1=1090+92+94+88+86+95+87+89+91+93=90.5
E
2
=
94
+
88
+
96
+
93
+
90
+
85
+
84
+
80
+
82
+
98
10
=
89
E_2=\frac{94+88+96+93+90+85+84+80+82+98}{10}=89
E2=1094+88+96+93+90+85+84+80+82+98=89
显然
E
1
>
E
2
E_1>E_2
E1>E2,通过观察可知语文成绩的离散程度小于数学成绩,故有
σ
1
<
σ
2
σ _1<σ _2
σ1<σ2。或者通过计算方差也可得出答案。



真题(2019-23)-数据分析-数据描述-平均值
23、某校理学院五个系每年录取人数如下表:
| 系数 | 数学系 | 物理系 | 化学系 | 生物系 | 地学系 |
|---|---|---|---|---|---|
| 录取人数 | 60 | 120 | 90 | 60 | 30 |
今年与去年相比,物理系平均分没交,则理学院录取平均分升高了。
(1) 数学系录取平均分升高了 3 分,生物系录取平均分降低了 2 分
(2) 化学系录取平均分升高了 1 分,地学系录取平均分降低了 4 分


2018
2017
2016
2015
2014
2013