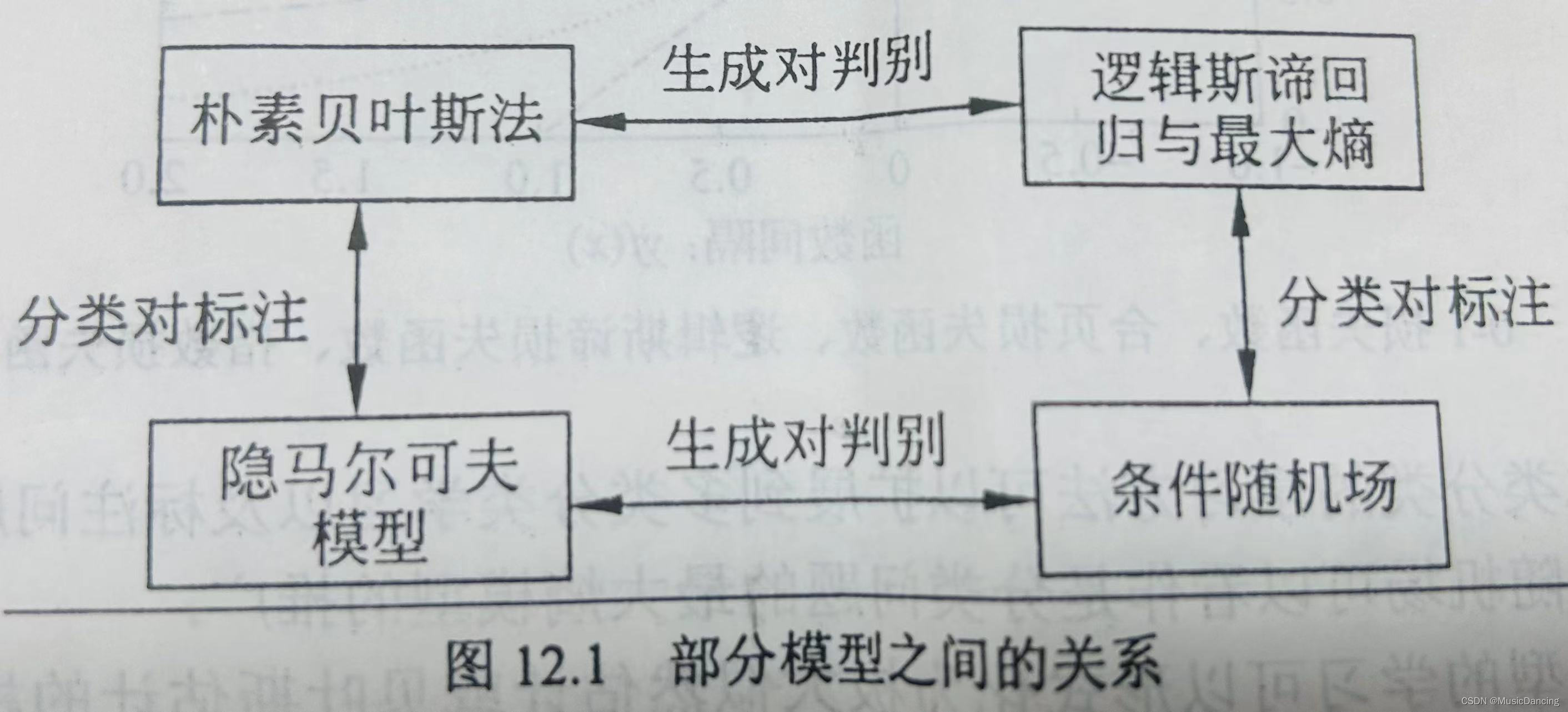
方差分析(ANOVA,也称变异数分析)是英国统计学家Fisher(1890.2.17-1962.7.29)提出的对两个或以上样本总体均值进行差异显著性检验的方法。
它的基本思想是将测量数据的总变异(即总方差)按照变异来源划分为组间效应和组内效应,进行估计,从而确定差异的显著性。根据考虑因素的数量,可方差分析分为单因素方差分析、二因素方差分析和多因素方差分析。
方法分析使用的前提条件与t检验相同,也需要满足样本正态分布,方差齐性的要求。以下我们分别对单因素方差分析和多因素方差分析进行介绍。
1.单因素方差分析(oneway anova)
只有一个因素(变量)的方差分析。对于只有两组数据的方差分析等价于t检验。以下为三组数据例子。
某工厂对三条流水线加工的产品进行8次抽样,产品有效成分(含量mg)如下表所示。试分析三条流水线的生产质量是否无差异。
流水线 样本 A [26.68, 26.01, 24.83, 25.05, 24.38, 24.1 , 26.38, 26.68] B [26.45, 25.68, 23.29, 27.01, 23.21, 25.24, 24.65, 26.39] C [24.49, 23.84, 25.87, 24.05, 24.1 , 25.64, 24.35, 25.07]
代码:
from statsmodels.api import stats
import numpy as np
#准备样本数据
X=np.array([[26.68, 26.01, 24.83, 25.05, 24.38, 24.1 , 26.38, 26.68],
[26.45, 25.68, 23.29, 27.01, 23.21, 25.24, 24.65, 26.39],
[24.49, 23.84, 25.87, 24.05, 24.1 , 25.64, 24.35, 25.07]])
#样本正太分布检验
stats.normaltest(X,axis=1)
#样本方差齐性检验
stats.levene(X[0],X[1],X[2])
#单因素方差分析.使用scipy.stats的f_oneway函数也行。但statsmodels的anova_oneway还可以进行方差不齐情况下的检验
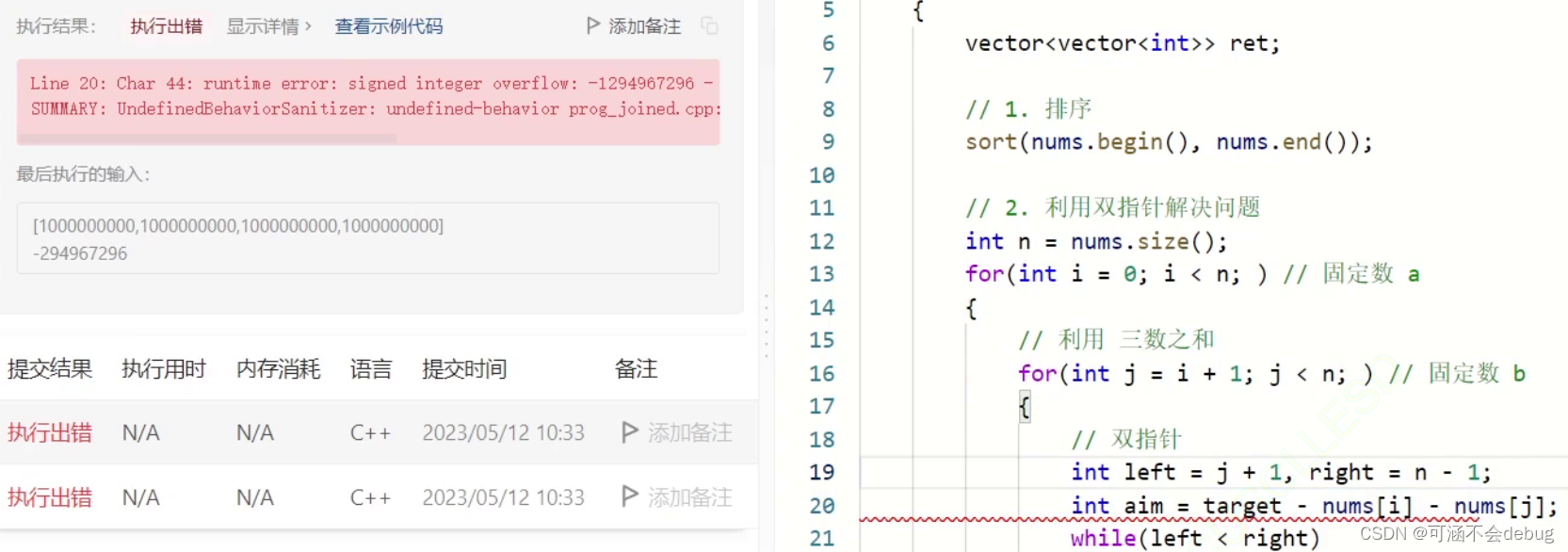
stats.anova_oneway(X,use_var="equal")上述三类检验的p值均大于0.05,说明可以使用方差检验且检验结果支持三条流水线产品质量无差异的假设。
2.多因素方差分析(anova)
多因素方差分析,用于研究一个因变量是否受到多个自变量(也称为因素)的影响。多因素方差分析既可以分析单个因素的作用(主效应),也可以分析因素之间的交互作用(交互效应)。如下例。
某工厂统计了多个工人使用不同机床的产品产量,试分析产量是否受工人技能和机床性能的影响。
我们仍然使用 statsmodels.api.stats统计学软件包进行处理,代码如下:
from statsmodels.api import stats
from statsmodels.formula.api import ols
#定义样本数据,当数据量比较大时,可以采用文件读取方式
X=pd.DataFrame(data=[('w1', 'm1', 20), ('w1', 'm2', 22), ('w1', 'm3', 24),
('w1', 'm4', 16), ('w1', 'm5', 26), ('w2', 'm1', 12),
('w2', 'm2', 10), ('w2', 'm3', 14), ('w2', 'm4', 4),
('w2', 'm5', 22), ('w3', 'm1', 20), ('w3', 'm2', 20),
('w3', 'm3', 18), ('w3', 'm4', 8), ('w3', 'm5', 16),
('w4', 'm1', 10), ('w4', 'm2', 12), ('w4', 'm3', 18),
('w4', 'm4', 6), ('w4', 'm5', 20), ('w5', 'm1', 14),
('w5', 'm2', 6), ('w5', 'm3', 10), ('w5', 'm4', 18),
('w5', 'm5', 10)],columns = ['Worker','Machine','Qnt'])
#构造线性回归表达式,用于方差分析
formula=ols('Qnt ~ Worker + Machine', data=X).fit()
#多因素方差分析
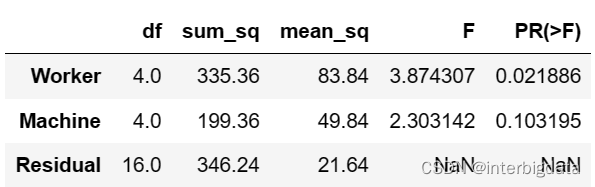
stats.anova_lm(formula) 结果如下:
最后一列为p值。可以看出不同工人的产量有差异(p=0.02<0.05),而不同机器上的产量差异不显著。
如果我们想进一步分析是哪几个工人的产量差异比较明显时,我们可以使用Tukey法进行多重差异性检验。代码如下:
from statsmodels.stats.multicomp import pairwise_tukeyhsd
#要注意,因变量要写在前面而自变量(因素)写在后面
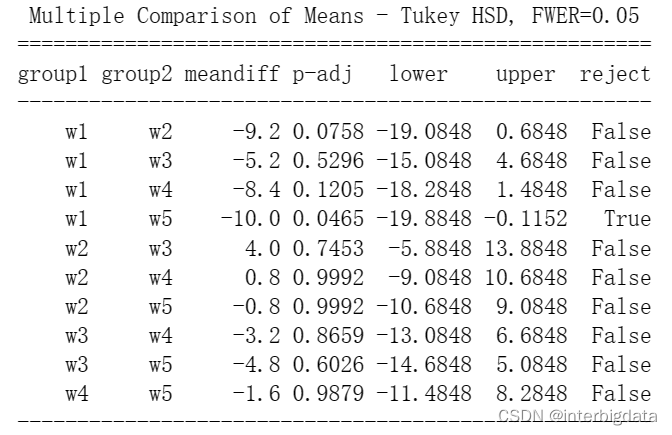
print(pairwise_tukeyhsd(X['Qnt'],X['Worker']))结果如下:
我们可以看出,w1,w5所在行的reject=True,说明两者的产量在总体水平估计上差异显著,产量均值之差为-10(),而其它工人之间产量差异不算显著。






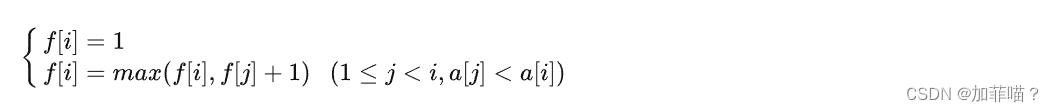

![[Linux] 基于LAMP架构安装论坛](https://img-blog.csdnimg.cn/direct/60e8bf1b62764a058afdce807b79234b.png)