开启蓝桥杯备战计划,每日练习算法一题!!坚持下去,想必下一年的蓝桥杯将会有你!!
笔者是在力扣上面进行的刷题!!由于是第一次刷题!找到的题目也不咋样!所以,就凑合凑合吧!笔者打算从数据结构开始刷起,毕竟现在刚刚接触到数据结构!!
在力扣上找到的刷题链接为:
https://leetcode.cn/study-plan/data-structures/?progress=yqv80ci
力扣是一个很不错的刷题平台!

偷懒了几天!!疫情发热,加咳嗽,精神不振!所以偷懒了呗!!感觉状态变好,所以快马加鞭!
36. 有效的数独
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true
实列2:
输入:board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

参考代码为:
class Solution {
public boolean isValidSudoku(char[][] board) {
int[][] rows = new int[9][9];//9行9个数
int[][] lows = new int[9][9];//9列9个数
int[][][] boxs=new int[3][3][9];//分小组后,行3个,列3个,每个小组9个数
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
char c = board[i][j];
if(c!='.'){
int index = c-'0'-1;//这里主要是字符与int类型计算,减1是为了计算数组中位置
rows[i][index]++;//在记录行的数组中统计这个数出现的次数
lows[j][index]++;//同理统计列
boxs[i/3][j/3][index]++;//同理计算块,这里有个求除数规则,可以将块做好标记,画图看下就明白了
//这里假设数独是规则的,则每个数在统计数组中不会出现大于1的情况
if(rows[i][index]>1||lows[j][index]>1||boxs[i/3][j/3][index]>1){
return false;
}
}
}
}
return true;
}
}这个列子有点儿稍微的难度!!毕竟,我也是看着解析来的!!!三维数组,是笔者从开始学习C语言,到目前的Java,数据结构是第一次用到!!尴尬了!!只能说,很少见吧!!!
73. 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示列1:

输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示列2:
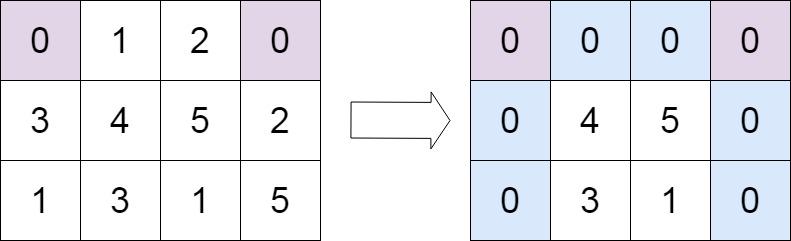
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1
进阶:
一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗
对于原地算法,或许有些人不是很了解,那么笔者帮助大家来看一下吧!!
一个算法有时候会不正当地被称为原地算法,只因为它用它的输出资料会覆盖掉它的输入资料。事实上这并不足够(在快速排序案例中所展示的)或是它所必须的;输出资料的空间可能是固定的,或如果以输出为串流资料而言,也甚至是可能无法被数清楚的。另一方面来看,有时候要决定一个算法是不是原地,而数它的输出空间可能是比较可行的,像是底下的第一个的 reverse 范例;如此使得它更难去严格地定义原地算法。在理论上的应用像是log-space reduction,更是典型的总是忽略输出的空间(在这些状况,更重要的是输出为仅能写入)
原文链接为:https://baike.baidu.com/item/%E5%8E%9F%E5%9C%B0%E7%AE%97%E6%B3%95
不懂的各位老铁,可以点进去进行看一下百度百科对原地算法的解释!!
使用标记数组
思路和算法
我们可以用两个标记数组分别记录每一行和每一列是否有零出现。
具体地,我们首先遍历该数组一次,如果某个元素为 00,那么就将该元素所在的行和列所对应标记数组的位置置为 \text{true}true。最后我们再次遍历该数组,用标记数组更新原数组即可。
参考代码为:
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
boolean[] row = new boolean[m];
boolean[] col = new boolean[n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == 0) {
row[i] = col[j] = true;
}
}
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (row[i] || col[j]) {
matrix[i][j] = 0;
}
}
}
}
}看着这个代码很是简单!!至少不是很难吧!!
两次遍历数组,第一次遍历数组的时候,找到数组中的含有0的元素的位置,将其所对应的行列置为true,第二次遍历数组的时候,就……然后就可以实现我们的目的了!!
看着很复杂,但是,也有很简单的哟!!