2021年认证杯SPSSPRO杯数学建模
D题 停车的策略
原题再现:
开车前往人流集中的目的地时,决定在何处停车经常是一个难题。是停在距离目的地较远的地方,因为那里的空余车位可能较多,然后再走很远的路?或者是否应该乐观一点,把车开到目的地附近,只寻找附近的停车位?如果采用后一种策略,如果目的地附近没有停车位,那么就必须回头去寻找更远的停车位,结果会更严重地浪费时间。
假设有一个足够大的停车场,停车位排列成一维的序列,目的地在序列的一端。我们不能居高临下地看到远处的车位情况,只能在开到车位附近时才能看清这里是否已被占据。图 1 是这个停车场的示意图,车辆从右向左进入,左侧的端点是目的地。
有人采用的策略是看到第一辆停着的车,就立即停到这辆车的右侧。这可以保证有位置,但显然会付出步行时间的代价。有人则将车一直向前开,直到左侧的端点,如果端点处没有空的停车位,再倒车到离目的地最近的空位(我们可以假设倒车不会影响后续车辆)。这可以找到当前离目的地最近的空位,但倒车也会损失时间,如果需要倒很远,带来的损失就更大了。还有人的策略是第一次看到有两个并排的空位时就停下来,如果开到最左端还没有看到,再采用倒车的办法。诸如此类。
第一阶段问题: 在题目中描述了三种停车的策略。请你和你的团队研究三种停车策略的效果好坏。包括如何衡量停车策略的效果,以及哪些参数影响了停车策略的效果?
整体求解过程概述(摘要)

问题分析:
在这道题目中,我们首先得到一条一维的停车场及三种停车策略,通过对题干内容的分析,我们选取驾驶者进入停车场的那一刻到抵达目的地的总用时T来评价停车策略的好坏。我们总结出三种停车策略,分别是第一种停车策略是进入停车场后如果看到空位就立即停入此车位,剩下的路程步行过去。第二种停车策略是进入停车场后一直直行,到达左侧端点之后如果此处没有空的停车位,倒车去找离此处最近的空的停车位,剩下的路程步行过去。第三种策略是进入停车场后如果发现有两处连续的空的停车位,立即在此处停车,剩下的步行过去。


通过查阅资料及定性分析,我们认为停车场的长度 L,停车位的总数量 m,某一停车位上无车的概率 p,这三个参数影响停车策略的效果,其中停车场的长度 L 和停车位的总数量 m 在一维的空间里存在着线性关系,最终我们决定分析停车位的总数量 m 和某一停车位上无车的概率 p 两个参数对停车策略的影响。
我们通过蒙特卡洛法模拟驾驶者停车的过程,首先建立一个概率模型,假设某一停车位上没有车的概率 X=p,那么 E(X)=停车场剩余停车位的数量,通过模拟多驾驶者停车的过程,统计出使用三种停车策略得到的总用时 T 的分布,分析 T 与评价指标的差异,来判定三种停车策略的优劣。
模型假设:
(1)假设模拟停车时,每一个停车位无车的概率是固定的
(2)假设停车场事一维的
(3)假设驾驶者开车速度固定,
(4)假设驾驶者步行速度固定
(5)假设倒车不会影响后续车辆
(6)假设每个停车位大小相同
模型的建立与求解


我们通过控制 n 和 p 的量来模拟不同的停车场,采用不同的 n 和 p,建立以下 6 种停车场
(1)p = 0.2 m = 100 第一种停车场
(1)P = 0.2 m = 200 第二种停车场
(1)P = 0.2 m = 300 第三种停车场
(1)P = 0.5 m = 100 第四种停车场
(1)P = 0.5 m = 200 第五种停车场
(1)P = 0.5 m = 300 第六种停车场
我们运用蒙特卡洛思想,模拟驾驶者在这 6 种停车场停车 100 次的情况,统计出运用三种停车策略下的停车用时分布。这里为了方便数据计算通过查阅资料统一停车位宽度取 2.7m,驾车速度取 8.3m/s,步行速度取 1.38m/s。
第一种停车策略 matlab 程序
m = 100
p = 0.2
x = randsrc(1, m,[0,1; p, (1 - p)])
zero_index = find(x == 0)
k = length(zero_index)
first_zero_index = zero_index(1)
for i = 1: m;
if i + 1 <= m& x(i) == 0;
t = 2.7 * (i/8.3 + (m - i)/1.38)
break
end
end
第二种停车策略 matlab 程序
m = 100
p = 0.5
x = randsrc(1, m,[0,1; p, (1 - p)])
zero_index = find(x == 0)
k = length(zero_index)
first_zero_index = zero_index(1)
for i = 1: m;
if x(i) == 0;
t = 2.7 * (m/8.3 + (m - i)/8.3 + (m - i)/1.38)
end
end
第三种停车策略 matlab 程序
m = 100
p = 0.2
x = randsrc(1, m,[0,1; p, (1 - p)])
zero_index = find(x == 0)
k = length(zero_index)
first_zero_index = zero_index(1)
for i = 1: m;
if i + 1 <= m& x(i) == 0& x(i + 1) == 0;
t = 2.7 * (i/8.3 + (m - i)/1.38)
break
end
end
第一种策略用时统计
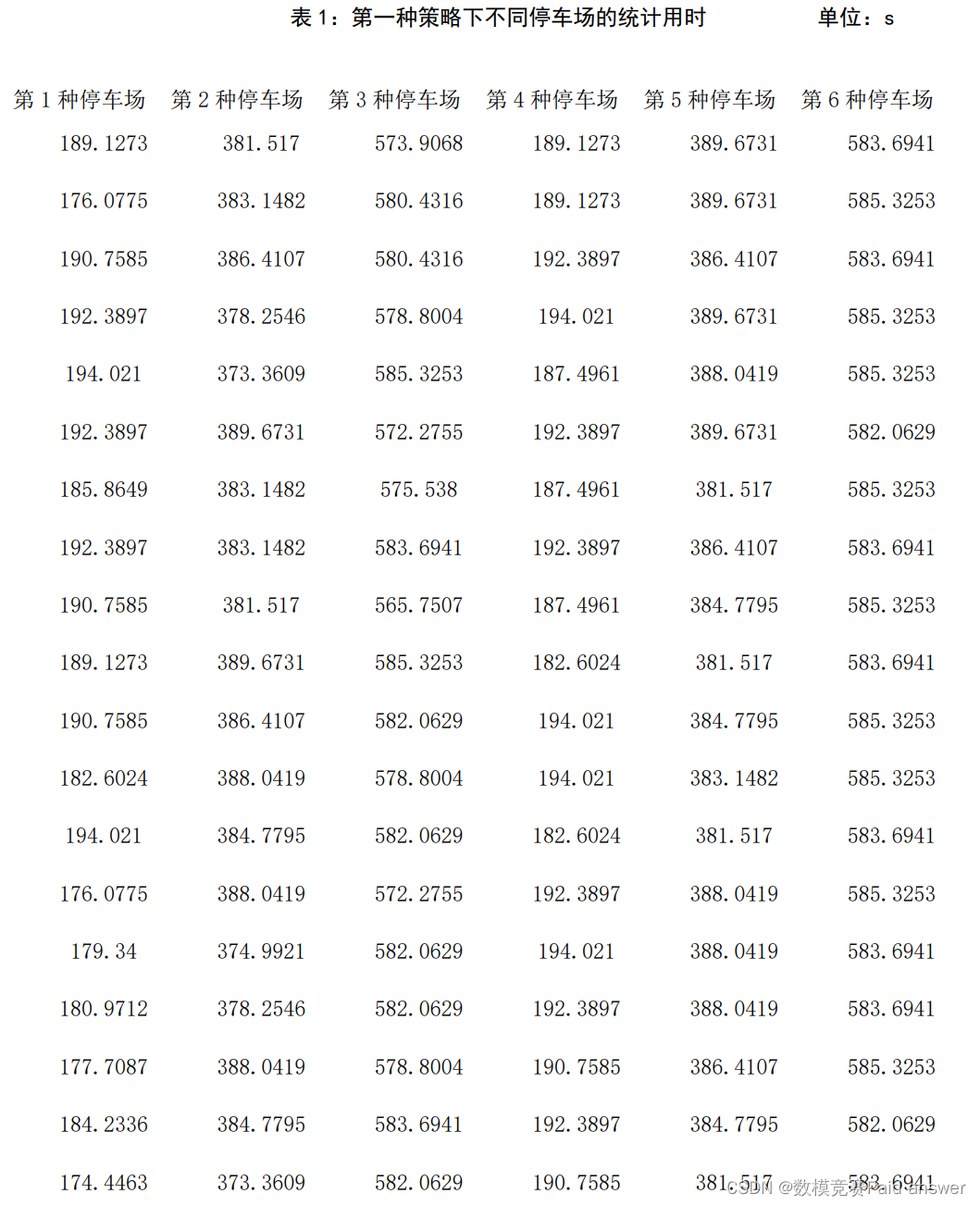
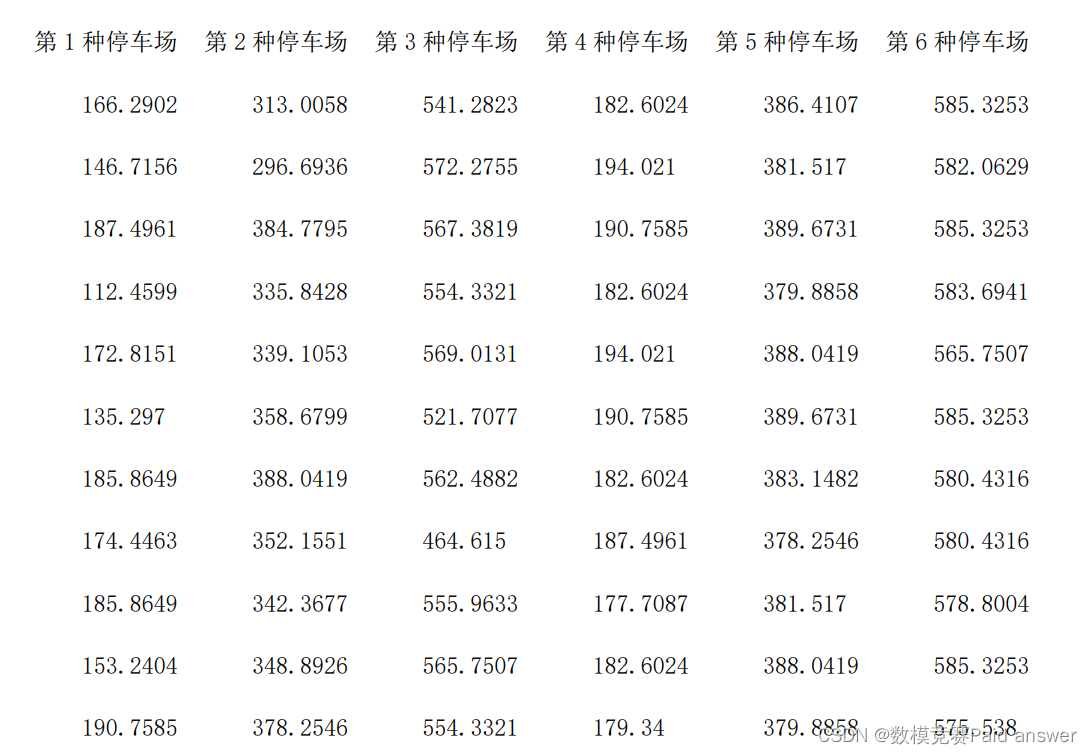
第二种策略用时统计

第三种策略用时统计
同一停车场不同策略用时统计图如下
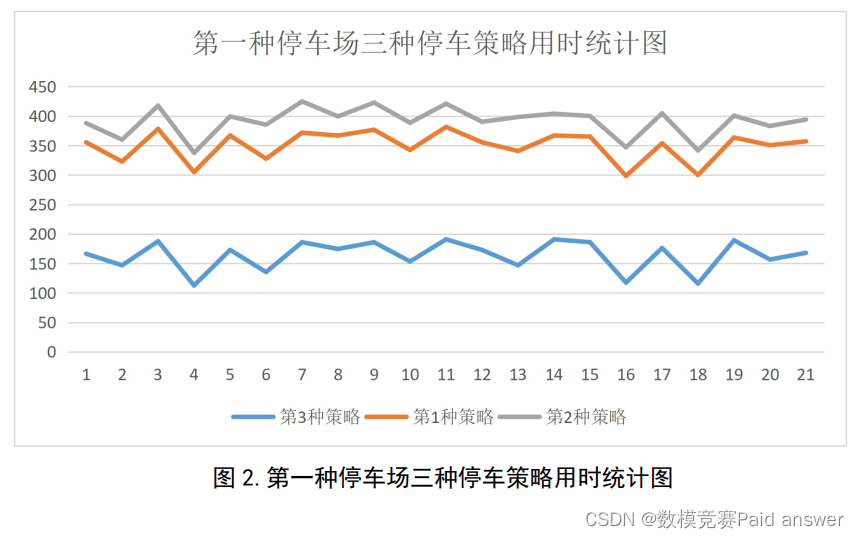
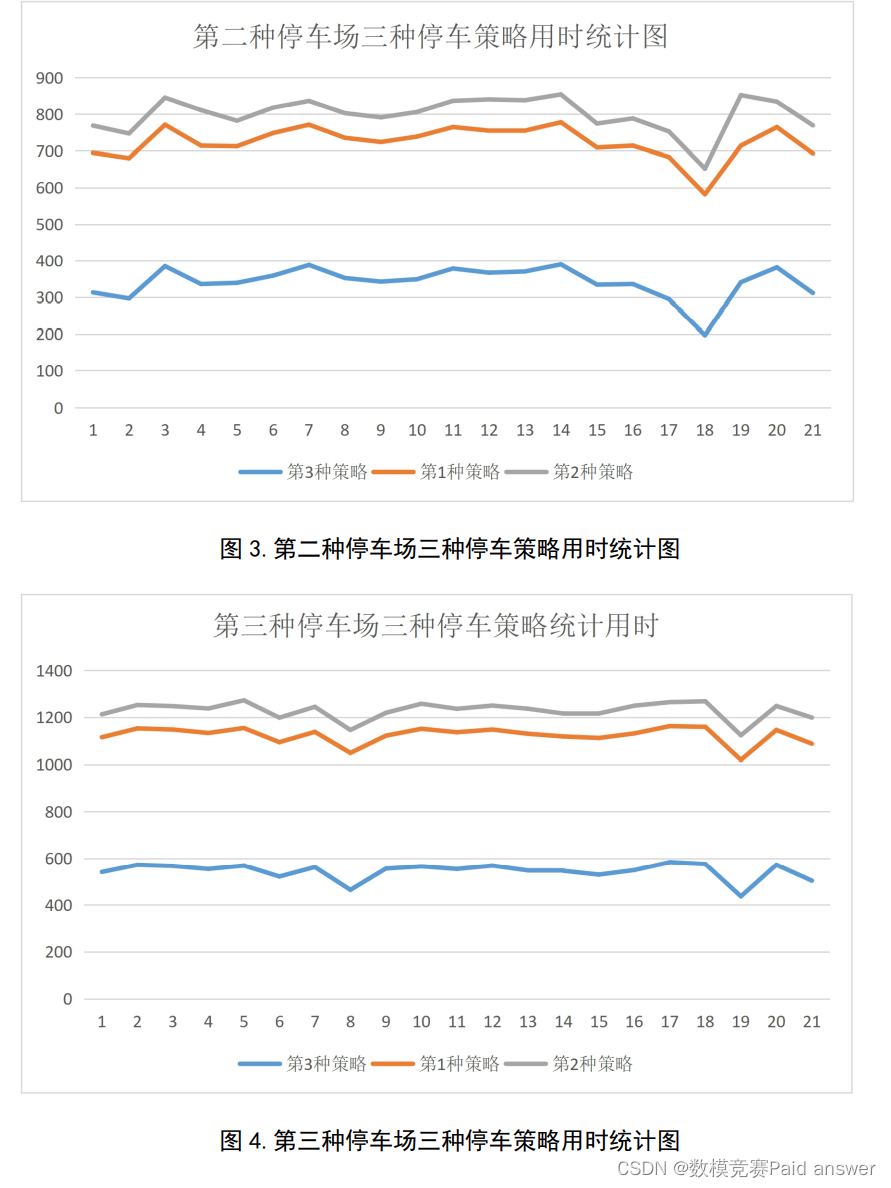
由上述图表可知第三种停车策略用时均小于Vb,而第二种策略用时小于Va的情况更多,而第一种策略均大于Va。同时p越大的时候,曲线趋于平稳,而此时第一种第二种停车策略用时反而更长,第三种停车策略用时会减少。而停车场数量越大,三种策略用时较Va相比增加的较多。
论文缩略图: