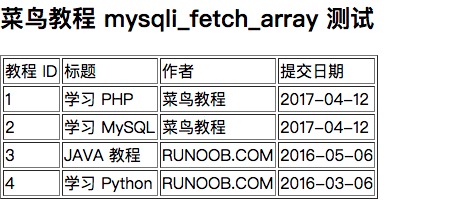
论文地址:https://openaccess.thecvf.com/content/CVPR2023/html/Cho_Learning_Adaptive_Dense_Event_Stereo_From_the_Image_Domain_CVPR_2023_paper.html
概述
事件相机在低光照条件下可以稳定工作,然而,基于事件相机的立体方法在域迁移时性能会严重下降。无监督领域自适应作为该问题的一种解决方法,传统的无监督自适应方法依赖于源域的标签值,但源域的视差标签值难以获取。针对该问题,文中提出一种新的无监督域自适应密集时间立体匹配方法(ADES)用于缓解目标域域源域之间的域偏差导致的模型性能下降问题。首先,文中提出一种自监督模块通过图像重建来训练在目标域的模型。与此同时,在源域上训练一个涂抹预测网络协助去除重建图像中的间歇性伪影。使用一个特征的归一化策略来沿着极线对齐匹配特征。最后,使用一个运动不变的一致性模块来在扰动运动之间实现一致性输出。实验结果表明,该模型在从普通图像域到事件相机图像域立体匹配的适应性上得到提升。

模型架构
模型主要包含三个部分:涂抹感知自监督模块、特征正则化、运动不变的一致性模块。涂抹感知自监督模块:该模块利用通过图像重建来利用图像的密集特征,从而在目标域的事件相机数据上训练模型。事件相机的数据是一种稀疏的数据表示,它异步地记录像素级的亮度变化信息(事件),而不是以固定的帧率捕获标准的强度图像。因此,只使用事件数据来重建图像时,在物体的边缘容易产生模糊混和失真的伪影,称之为涂抹效应。这种涂抹效应会影响视差预测的精度。为了预测目标域中的涂抹效应,作者在源域的图像数据引入一个模块来估计和抑制重建图像的涂抹效应。此外,作者在构建代价体之间使用特征归一化对匹配特征进行归一化处理。特征归一化化策略常被用于图像模态的域自适应过程中,由于事件相机成像的特殊性(如天空之类的区域事件的稀疏性),对整个像素区域归一化并不高效,传统的归一化方法可能会误导模型偏向于没有事件发生的区域的值。为了减少源域与目标域之间像素的差异,作者沿着极线方向来对特征进行归一化。针对由事件相机运动引起的域偏差,作者提出运动不变一致性模块来预测一致的视差。

给定输入源域的图像对
(
I
l
t
−
1
,
I
r
t
−
1
)
,
(
I
l
t
,
I
r
t
)
(I_l^{t-1}, I_r^{t-1}), (I_l^{t}, I_r^{t})
(Ilt−1,Irt−1),(Ilt,Irt) 与对应的视差标签
d
~
l
t
\tilde{d}_l^t
d~lt,模型的目标是在目标域中从事件流
E
l
t
^
,
E
r
t
^
E_{l}^{\hat{t}},E_{r}^{\hat{t}}
Elt^,Ert^ 预测
t
^
\widehat{t}
t
时刻的视差
D
l
t
^
D_{l}^{\hat{t}}
Dlt^(源域与目标域的样本非匹配),使用体素网格来表示事件流(使用
V
l
t
^
V_l^{\hat{t}}
Vlt^ 来代表
E
l
t
^
E_l^{\hat{t}}
Elt^)。
ADES(Adaptive Dense Event Stereo)主要包含三个模块:涂抹感知自监督模块、特征归一化模块、运动不变一致性模块。在源域,使用一个预训练好的“视频到事件”重建模型(
G
I
→
E
\mathcal{G}_{I\to E}
GI→E)来从左右图像序列中提取事件表征:
V
l
t
=
G
I
→
E
(
I
l
t
−
1
,
I
l
t
)
,
V
r
t
=
G
I
→
E
(
I
r
t
−
1
,
I
r
t
)
.
V_l^t=\mathcal{G}_{I\to E}(I_l^{t-1},I_l^t),V_r^t=\mathcal{G}_{I\to E}(I_r^{t-1},I_r^t).
Vlt=GI→E(Ilt−1,Ilt),Vrt=GI→E(Irt−1,Irt). 将源域生成的体素网格对
(
V
l
t
,
V
r
t
)
(V_{l}^{t},V_{r}^{t})
(Vlt,Vrt) 与目标域中的体素网格对
(
V
l
t
^
,
V
r
t
^
)
(V_l^{\hat{t}},V_r^{\hat{t}})
(Vlt^,Vrt^) 同时送入权值共享的事件流立体匹配模型,在此过程中,作者使用特征归一化来降低域偏差带来的影响。对源域样本对应的视差标签来计算视差损失,使用涂抹感知自监督模块与运动不变一致性模块来对目标域样本的结果计算损失。
Smudge-aware Self-supervision Module (SSM):涂抹感知自监督模块
该模块旨在使用光度一致性重建的自监督的子任务来提高模型的域自适应能力,如图3下方所示。
使用一个预训练好的“事件到图像”的网络来将目标域的体素网格映射到图像空间,而在此过程中在图像中的物体边缘会出现模糊,称之为涂抹现象。为此,在目标域训练一个涂抹感知自监督模块来预测涂抹的区域。
在源域中,如图3上方所示,作者通过随机扭曲域模糊对图像进行增强来模拟涂抹效应的影响。为了模拟由传感器噪声在物体边缘产生的涂抹影响,作者使用超像素算法来解析区域而不是随机选取的矩形区域进行模糊增强 (因为超像素的边缘通常位于物体的边界上,从而更好地反映了由于传感器噪声而在物体边界处产生的涂抹效果)。继而使用一个轻量化的U-Net来预测预测涂抹区域,并使用二元交叉熵损失来计算损失:
L
s
o
u
r
c
e
m
a
s
k
=
∑
i
∈
{
l
,
r
}
B
C
E
(
M
i
t
,
M
~
i
t
)
.
\mathcal{L}_{source}^{mask}=\sum_{i\in\{l,r\}}BCE(M_{i}^{t},\tilde{M}_{i}^{t}).
Lsourcemask=∑i∈{l,r}BCE(Mit,M~it).
在目标域,如图3下方所示,作者使用权值共享的涂抹区域预测网络来从重建图像
I
^
l
t
^
,
I
^
r
t
^
\hat{I}_{l}^{\hat{t}},\hat{I}_{r}^{\hat{t}}
I^lt^,I^rt^ 预测涂抹区域
M
l
t
^
,
M
r
t
^
∈
[
0
,
1
]
M_{l}^{\hat{t}},M_{r}^{\hat{t}}\in[0,1]
Mlt^,Mrt^∈[0,1],将
I
^
r
t
^
\hat{I}_{r}^{\hat{t}}
I^rt^ 根据目标域预测的视差图
D
l
t
^
D_{l}^{\hat{t}}
Dlt^来warp到左视图得到
W
ˉ
r
→
l
(
I
^
r
t
^
)
\bar{W}_{r\to l}(\hat{I}_r^{\hat{t}})
Wˉr→l(I^rt^)。考虑到左右驶入的涂抹mask图像,光度一致性误差定义为:
L
t
a
r
g
e
t
r
e
c
o
n
=
α
1
−
SSIM
(
I
^
l
t
^
⊙
M
t
^
,
W
r
→
l
(
I
^
r
t
^
)
⊙
M
t
^
)
2
+
(
1
−
α
)
∥
I
^
l
t
^
⊙
M
t
^
−
W
r
→
l
(
I
^
r
t
^
)
⊙
M
t
^
∥
1
,
(1)
\begin{aligned} \mathcal{L}_{target}^{recon}& =\alpha\frac{1-\text{SSIM}(\hat{I}_{l}^{\hat{t}}\odot M^{\hat{t}},W_{r\to l}(\hat{I}_{r}^{\hat{t}})\odot M^{\hat{t}})}{2} +(1-\alpha)\|\hat{I}_{l}^{\hat{t}}\odot M^{\hat{t}}-W_{r\to l}(\hat{I}_{r}^{\hat{t}})\odot M^{\hat{t}}\|_{1}, \end{aligned}\tag{1}
Ltargetrecon=α21−SSIM(I^lt^⊙Mt^,Wr→l(I^rt^)⊙Mt^)+(1−α)∥I^lt^⊙Mt^−Wr→l(I^rt^)⊙Mt^∥1,(1)
其中,
M
t
^
=
1
−
(
M
l
t
^
⊙
W
r
→
l
(
M
r
t
^
)
)
,
\begin{aligned}M^{\hat{t}}=1-(M_{l}^{\hat{t}}\odot W_{r\to l}(M_{r}^{\hat{t}})),\end{aligned}
Mt^=1−(Mlt^⊙Wr→l(Mrt^)),
⊙
\odot
⊙ 表示逐元素相乘。SSIM 表示结构一致性损失,
α
=
0.85
\alpha=0.85
α=0.85。
Feature Normalization 特征归一化
为了减小源域与目标域之间的域偏差,作者使用了特征级归一化方法来对特征增强。但考虑到不同区域事件的稀疏性(在图像上方的天空区域事件较少,而在图像下方的建筑的事件较多)以及极线校正图像的特殊性,作者只沿着极线方向在事件发生的区域进行特征归一化,先沿着通道维度进行归一化:
F
(
k
,
i
,
j
)
=
F
(
k
,
i
,
j
)
∑
c
=
0
C
−
1
∥
F
(
c
,
i
,
j
)
∥
2
+
ε
⋅
(2)
F(k,i,j)=\frac{F(k,i,j)}{\sqrt{\sum_{c=0}^{C-1}\left\|F(c,i,j)\right\|^2+\varepsilon}}\cdotp \tag{2}
F(k,i,j)=∑c=0C−1∥F(c,i,j)∥2+εF(k,i,j)⋅(2)
继而沿着极线方向归一化:
F
(
k
,
i
,
j
)
=
F
(
k
,
i
,
j
)
∑
w
=
0
W
−
1
∥
F
(
k
,
i
,
w
)
∥
2
+
ε
.
(3)
\begin{aligned}F(k,i,j)&=\frac{F(k,i,j)}{\sqrt{\sum_{w=0}^{W-1}\left\|F(k,i,w)\right\|^2+\varepsilon}}.\end{aligned}\tag{3}
F(k,i,j)=∑w=0W−1∥F(k,i,w)∥2+εF(k,i,j).(3)
Motion-invariant Consistency Module (MCM) 运动不变的一致性模块
该模块旨在解决由不同相机运动引起的域偏差和增强模型对扰动与噪声的鲁棒性。将
T
T
T 时间内累积的事件
V
l
t
^
,
T
,
V
r
t
^
,
T
V_l^{\hat{t},T},V_r^{\hat{t},T}
Vlt^,T,Vrt^,T 送入视差预测模型中得到视差图
D
l
t
^
.
D_{l}^{\hat{t}}.
Dlt^. 由于现有的数据集中运动是固定且无法改变的,作者引入一个时间扰动参数
τ
\tau
τ 来增强快事件流。若事件数据在
T
+
τ
T+\tau
T+τ 时间内积累,将其沿着时间通道归一化到0-1,并转换为体素网格后可以模仿快速运动中的事物的事件体素网格。若事件数据在
T
−
τ
T-\tau
T−τ 时间内积累,则与慢速运动产生的体素网格相同,如图5所示:

将
V
l
t
^
,
T
^
,
V
r
t
^
,
T
^
V_l^{\hat{t},\hat{T}},V_r^{\hat{t},\hat{T}}
Vlt^,T^,Vrt^,T^ 送入事件立体匹配模型中得到视差图
D
~
l
t
^
.
\tilde{D}_l^{\hat{t}}.
D~lt^.,使用
L
1
L_1
L1 损失来约束增强前后生成的视差图:
L t a r g e t c o n s i s t e n c y = ∥ D l t ^ − D ~ l t ^ ∥ 1 (4) \mathcal{L}_{target}^{consistency}=\|D_l^{\hat{t}}-\tilde{D}_l^{\hat{t}}\|_1\tag{4} Ltargetconsistency=∥Dlt^−D~lt^∥1(4)
损失函数
在源域,使用平滑 L 1 L1 L1 损失来约束视差估计模型: L s o u r c e t a s k = smooth L 1 ( d ~ l t − d l t ) \mathcal{L}_{source}^{task}=\text{ smooth}_{L_1}(\tilde{d}_l^t-d_l^t) Lsourcetask= smoothL1(d~lt−dlt), 使用二元交叉熵损失来约束涂抹区域: L s o u r c e m a s k = ∑ i ∈ { l , r } B C E ( M i t , M ~ i t ) . \mathcal{L}_{source}^{mask}=\sum_{i\in\{l,r\}}BCE(M_{i}^{t},\tilde{M}_{i}^{t}). Lsourcemask=∑i∈{l,r}BCE(Mit,M~it).
L
t
o
t
a
l
=
L
s
o
u
r
c
e
t
a
s
k
+
λ
1
L
s
o
u
r
c
e
m
a
s
k
+
λ
2
L
t
a
r
g
e
t
r
e
c
o
n
+
λ
3
L
t
a
r
g
e
t
c
o
n
s
i
s
t
e
n
c
y
,
\begin{aligned}\mathcal{L}^{total}=\mathcal{L}_{source}^{task}+\lambda_1\mathcal{L}_{source}^{mask}+\lambda_2\mathcal{L}_{target}^{recon}+\lambda_3\mathcal{L}_{target}^{consistency},\end{aligned}
Ltotal=Lsourcetask+λ1Lsourcemask+λ2Ltargetrecon+λ3Ltargetconsistency,
实验结果