极限学习机ELM回归预测（MATLAB代码实现）

news2024/9/28 17:25:57

🍒🍒🍒欢迎关注🌈🌈🌈

📝个人主页：我爱Matlab

👍点赞➕评论➕收藏 == 养成习惯（一键三连）🌻🌻🌻

🍌希望大家多多支持🍓~一起加油 🤗

💬语录：将来的我一定会感谢现在奋斗的自己！

🍁🥬🕒摘要🕒🥬🍁

极限学习机（Extreme Learning Machine,ELM）作为前馈神经网络学习中一种全新的训练框架,在行为识别、情感识别和故障诊断等方面被广泛应用,引起了各个领域的高度关注和深入研究.ELM最初是针对单隐层前馈神经网络的学习速度而提出的,之后又被众多学者扩展到多隐层前馈神经网络中.该算法的核心思想是随机选取网络的输入权值和隐层偏置,在训练过程中保持不变,仅需要优化隐层神经元个数.网络的输出权值则是通过最小化平方损失函数,来求解Moore-Penrose广义逆运算得到最小范数最小二乘解.相比于其它传统的基于梯度的前馈神经网络学习算法,ELM具有实现简单,学习速度极快和人为干预较少等显著优势,已成为当前人工智能领域最热门的研究方向之一.ELM的学习理论表明,当隐层神经元的学习参数独立于训练样本随机生成,只要前馈神经网络的激活函数是非线性分段连续的,就可以逼近任意连续目标函数或分类任务中的任何复杂决策边界.近年来,随机神经元也逐步在越来越多的深度学习中使用,而ELM可以为其提供使用的理论基础.

✨🔎⚡运行结果⚡🔎✨

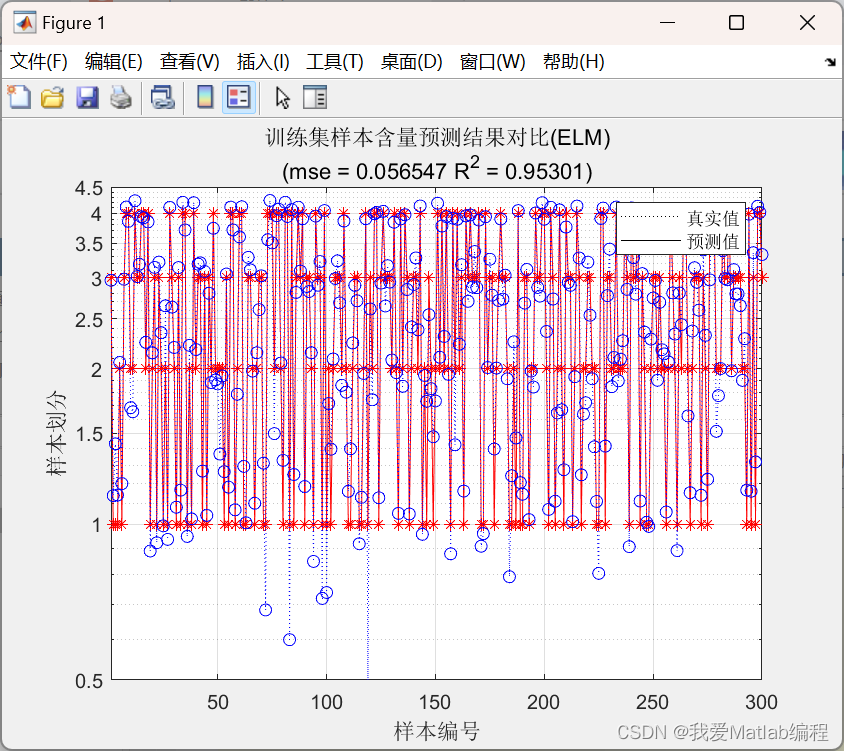
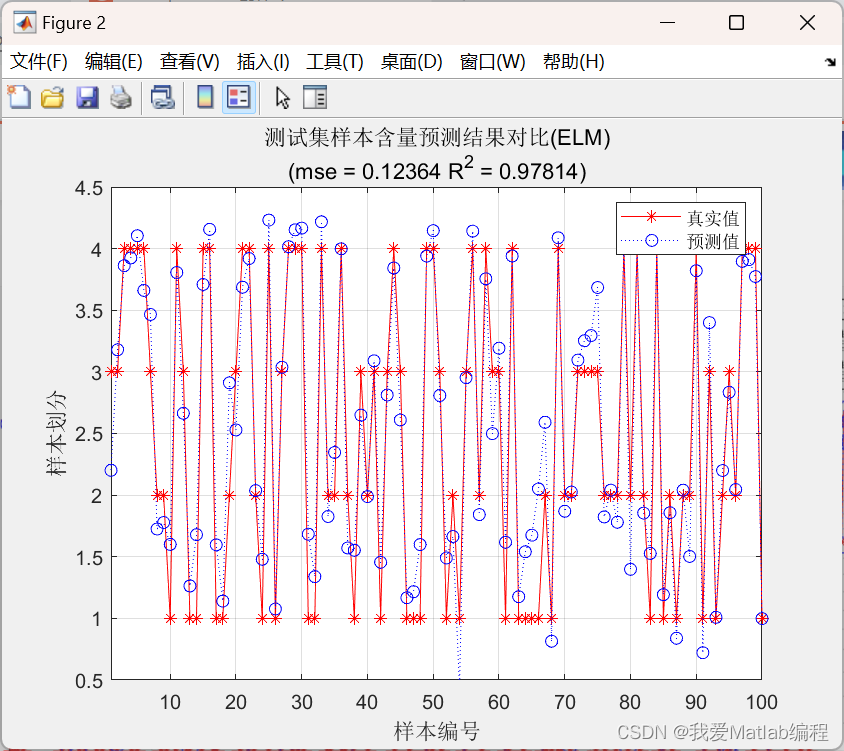
💂♨️👨‍🎓Matlab代码👨‍🎓♨️💂

完整代码：

%% 训练集/测试集产生
load('RAW.mat');
RAW1=RAW(:,:);
RAW=RAW1(:,1:254);
LLL=RAW1(:,255);
[oo, pp]=size(RAW);
temp = randperm(oo);%训练集和预测集按照3:1分类
P_train = RAW(temp(1:300),:)';
T_train = LLL(temp(1:300),:)';
P_test = RAW(temp(301:end),:)';
T_test = LLL(temp(301:end),:)';

%% ELM创建/训练
[IW,B,LW,TF,TYPE] = elmtrain(P_train,T_train,80,'sig',0);

%% ELM仿真测试
T_sim_1 = elmpredict(P_train,IW,B,LW,TF,TYPE);
T_sim_2 = elmpredict(P_test,IW,B,LW,TF,TYPE);

%% 结果对比
result_1 = [T_train' T_sim_1'];
result_2 = [T_test' T_sim_2'];

% 训练集均方误差
E = mse(T_sim_1-T_train);
% 训练集决定系数
N = length(T_train);
R2=(N*sum(T_sim_1.*T_train)-sum(T_sim_1)*sum(T_train))^2/((N*sum((T_sim_1).^2)-(sum(T_sim_1))^2)*(N*sum((T_train).^2)-(sum(T_train))^2));

% 预测集均方误差
E1 = mse(T_sim_2-T_test);
% 预测集决定系数
N1=length(T_test);
R21=(N*sum(T_sim_2.*T_test)-sum(T_sim_2)*sum(T_test))^2/((N*sum((T_sim_2).^2)-(sum(T_sim_2))^2)*(N*sum((T_test).^2)-(sum(T_test))^2));

%% 绘图
figure(1)
plot(1:N,T_train,'r-*',1:N,T_sim_1,'b:o');
axis([1,300,0.5,4.50]);
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('样本划分')
string = {'训练集样本含量预测结果对比(ELM)';['(mse = ' num2str(E) ' R^2 = ' num2str(R2) ')']};
title(string)

figure(2)
plot(1:N1,T_test,'r-*',1:N1,T_sim_2,'b:o');
axis([1,100,0.5,4.50]);
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('样本划分')
string = {'测试集样本含量预测结果对比(ELM)';['(mse = ' num2str(E1) ' R^2 = ' num2str(R21) ')']};
title(string)