🏆前言:文章回顾了深度学习在SfM中的应用,并提出了一种新的深度两视图SfM框架。该框架结合了深度学习和经典SfM几何算法的优点。在各个数据集上取得较好的结果。
文章目录
- 解决的问题
- 基本流程
- 实施细节
- 光流估计
- 相机位姿估计
- 尺度不变的深度估计
- 损失函数
- 总结
- 参考资料

会议/期刊:2021CVPR
论文题目:《Deep Two-View Structure-from-Motion Revisited》
论文链接:[2104.00556] Deep Two-View Structure-from-Motion Revisited (arxiv.org)
开源代码:jytime/Deep-SfM-Revisited (github.com)
解决的问题
- 传统的SfM算法只能恢复相对相机运动和相对场景深度。在没有场景比例或可识别对象的先验知识的情况下,无法推断出绝对比例。并且传统的匹配算法在非朗伯曲面、模糊曲面和无纹理曲面上往往存在精度低的问题。
- 随着深度学习的兴起,最近一些研究人员探索了基于神经网络的两视图SfM的解决方案。这些方法中的大多数可分为以下两类。
- 在第一类中,我们将其称为类型I(如下图中的a),该问题被视为单目深度和姿态回归的联合优化任务,具体地说,它使用了两种网络:一种是从一幅图像中估计出符合标准的深度,另一种是根据两幅输入图像预测出符合标准的摄像机姿态。在推理过程中,两个网络都独立运行。比如SfMLearner、GeoNet等
- 在表示为类型II的第二类中(如下图中的b),从图像对推断经缩放的相机姿势和经缩放的深度,并通过多视点几何进行迭代细化。这类方法包括DeMoN、BANet、DeepV2D、DeepSFM等
- 虽然深度学习的能力使类型I和类型II都能获得较好的结果,但我们注意到它们难以解决ill-posed问题(依据Ill-posed problems in early vision论文所述,ill-posed problem包括the recovery of motion and optical flow, shape from shading, surface interpolation, and edge detection等)
基本流程
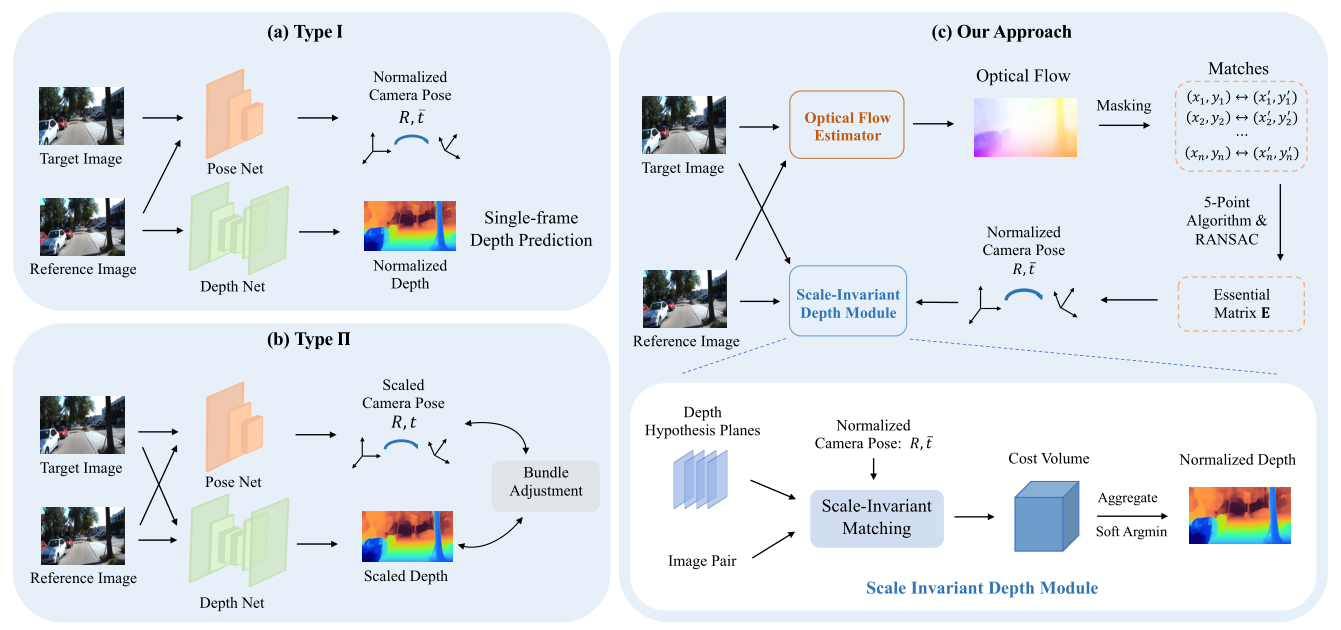
如上图c,Deep-SfM-Revisited流程总结为:
- 匹配帧之间的对应点,
- 估计基本矩阵,从而估计相对相机姿态,
- 估计高达未知比例因子的密集深度图
具体来说:
- 使用深度光流网络估计两帧之间的密集匹配点,然后采样一组高度可匹配点
- 使用经过GPU加速的经典五点RANSAC算法计算相机的相对位姿
- 由于这些相机的相对位姿具有尺度不确定性,所以估计的深度也会受到尺度不确定性的影响。因此,为了groundtruth来监督估计的尺度不确定性深度,论文提出了一种结合尺度特定损失的尺度不变性深度估计网络来估计最终的相对深度图
- 由于存在相机相对位姿,所以深度估计网络受极线约束的影响,从而得到一个更高的精度
实施细节
光流估计
深度光流方法可以处理大位移以及无纹理、遮挡和非朗伯曲面,弥补了传统方法的缺点。注意,作者使用DICLFlow在两个连续的帧之间生成密集的匹配点。光流估计的目的是为了下一步更好的相机位姿估计
相机位姿估计
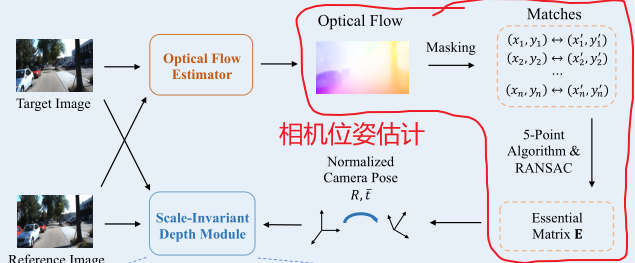
与以前所有基于深度学习的从输入图像回归相机位姿的方法不同,论文使用匹配点来计算相机位姿。
关键问题是:如何从光流中稳健地过滤掉噪声密集的匹配,以仅保留高质量的匹配?
作者发现,只需简单地使用SIFT关键点位置(注意,这里不是使用SIFT进行匹配)生成mask(即保留图像中的SIFT关键点),即可在所有数据集中都获得很好的结果。因为光流在纹理丰富的区域可以获得更准确的结果,mask内各个经过光流匹配的SIFT关键点,由经过GPU加速的RANSAC进行过滤(这种方法可以避免帧间运动物体的干扰),在获得基本矩阵E后,将使用矩阵分解恢复相机姿态(R,t)
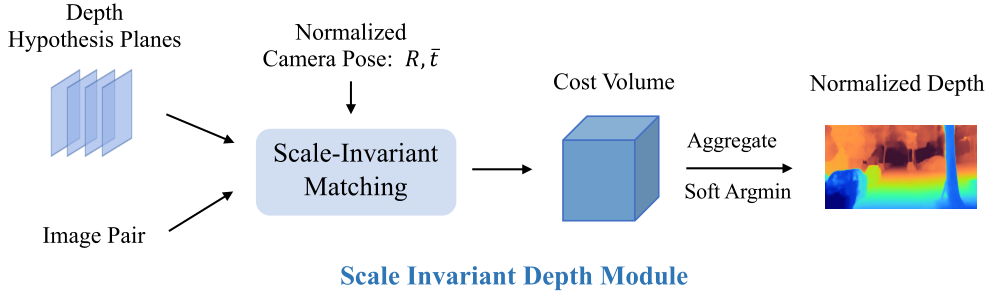
尺度不变的深度估计
论文提出了一种Scale-Invariant Matching方法来恢复尺度模糊的密集深度图,具体来说:
-
给定一个像点x,生成L个匹配候选点。
-
在标准平面扫描问题中,匹配候选对象的采样分布根据比例因子α而变,如下图所示。
-
此外,由于不知道问题中的绝对尺度,论文将平移向量t进行了归一化。
-
然后,将预测的深度d固定住,那么匹配候选点的分布就是尺度不变的了。
-
最后,为了使估计深度和深度真值兼容,需要相应地对估计深度进行缩放来匹配深度真值;如下, α g t \alpha_{\mathrm{gt}} αgt表示相对深度到绝对深度的缩放因子
d ∼ α g t d ^ \mathbf{d} \sim \alpha_{\mathrm{gt}} \hat{\mathbf{d}} d∼αgtd^

这种尺度不变方法在本论文起着至关重要的作用,因为它使深度估计网络不再受到尺度模糊问题的困扰。先前的算法无法从尺度不变匹配中受益,因为他们通常通过CNN直接预测绝对比例来避免尺度模糊问题。
损失函数
上面的尺度变换因子
α
g
t
\alpha_{\mathrm{gt}}
αgt将用于构建深度估计的损失函数,论文中使用Huber损失来计算预测深度和深度真值之间的差异:
L
depth
=
∑
x
ℓ
huber
(
α
g
t
d
^
x
−
d
x
)
\mathcal{L}_{\text {depth }}=\sum_{\mathbf{x}} \ell_{\text {huber }}\left(\alpha_{\mathrm{gt}} \hat{\mathbf{d}}_{\mathbf{x}}-\mathbf{d}_{\mathbf{x}}\right)
Ldepth =x∑ℓhuber (αgtd^x−dx)
如果相机位姿真值和深度真值都给定,还可以通过计算2D点的刚性流(rigid flow)来更新光流网络:
L
flow
=
∑
(
u
^
x
−
u
x
)
2
\mathcal{L}_{\text {flow }}=\sum\left(\hat{\mathbf{u}}_{\mathbf{x}}-\mathbf{u}_{\mathbf{x}}\right)^{2}
Lflow =∑(u^x−ux)2
总结
- 文章回顾了深度学习在SfM中的应用,并提出了一种新的深度两视图SfM框架。该框架结合了深度学习和经典SfM几何算法的优点
- 使用深度光流方法估计SIFT匹配点,可以处理大位移以及无纹理、遮挡和非朗伯曲面,弥补了传统方法的缺点
- 经过光流匹配的SIFT关键点将会被赋予mask,由经过GPU加速的RANSAC进行过滤,这种方法可以避免帧间运动物体的干扰
- 提出了一种尺度不变的深度估计模块,来处理groundtruth深度与预测的深度之间的尺度不匹配的问题
参考资料
2021年CVPR论文Deep Two-View Structure-from-Motion Revisited阅读笔记_zeeq_的博客-CSDN博客_deep two-view structure-from-motion revisited